多层电磁屏蔽的电磁拓扑 分析方法

摘要： 提出了一种用于多层电磁屏蔽条件下分析系统电子器件之间相互耦合的电磁拓扑模型。将该模型与求第k最短路算法结合，得出在不同频率范围下求从源点到终点屏蔽系数小于规定值路径的算法，得到需要改进的电磁耦合路径。该算法是通过对第k最短路算法修改而得到的，不需要求最小树和时间复杂度。仿真实验证明该算法是有效的，可以用于大型复杂电子系统耦合问题的分析。

关键词： 多层屏蔽； 电磁拓扑； 最短路径

     随着电子技术的不断发展和应用，电磁干扰问题也越来越严重，特别是当干扰源为高功率微波脉冲时，甚至可以烧毁电子器件[1]。另一方面由于电子系统的规模越来越大，结构越来越复杂，电子系统的各个部件间的相互耦合也使系统间的电磁干扰增多。屏蔽腔是用来减小电磁干扰的有效方法，由于在屏蔽腔上一般都不可避免地开有用于电源线连接、通风或其他用途的孔缝或孔隙，降低了屏蔽腔的屏蔽作用，使电磁耦合进入腔内，影响电子设备的正常工作。因此，必须研究在多层屏蔽条件下大型复杂电子系统的各个电子器件间的交互作用，找出总屏蔽系数不符合规定要求的路径，对这些路径进行特别电磁防护，使其达到设计要求。

1 电磁屏蔽拓扑模型

     许多重要的大型复杂电子系统，为了使其在强电磁干扰条件下仍能正常工作，往往对其进行多层电磁防护。以双层屏蔽为例来说明如何建立多层电磁屏蔽条件下的电磁拓扑模型。假设采用一个简化的电脑机箱，对其进行双重防护，其电子设备和对应的电磁屏蔽拓扑图分别如图1，图2所示。

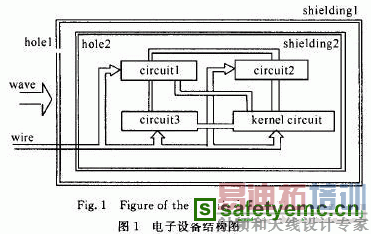
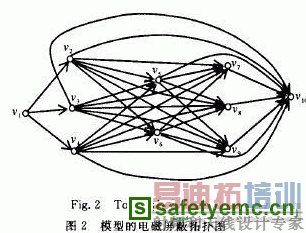
    图2中 对应入射电磁波， 。～ 分别对应孔1、屏蔽层1、电线； ～ 分别对应孔2、屏蔽层2； ～ 。分别对应电路1(光驱)、电路2(软驱)、电路3(硬盘)； 对应核心电路(主板)。边 ，赋权为顶点 与顶点， 间的屏蔽系数，是入射电磁波频率的函数，每边加权值都是变化的。在进行系统间耦合分析时，需要针对不同的频率值才能进行准确的计算。当有多个屏蔽层时，只需在相应的电磁拓扑图中添加相应的顶点和边即可。值得注意的是，此时，确定顶点 与顶点 j间的屏蔽系数是比较困难的。本文旨在已知各顶点间的屏蔽系数的条件下，寻找从源点到终点的总屏蔽系数不满足要求的路径。在利用电磁屏蔽拓扑图进行系统耦合的分析和设计时，往往要求从源点到终点的所有路径的总屏蔽系数达到规定值。文献[2]运用Dijkstra算法给出了总屏蔽系数和最小的路径。文献1-3]运用MPS算法找出所有总屏蔽系数和不满足要求的路径，但MPS算法执行时，首先要求给出电磁屏蔽拓扑图中的最小树 ，而求最小树 并非易事。本文给出另一种求总屏蔽系数和不满足要求的所有路径的算法。该算法通过修改第忌最短路算法实现 。

2 算法描述

    根据本文提出的算法，找出总屏蔽系数小于15 dB的路径有：

针对不符合要求的路径进行改进，即可使系统达到电磁防护的设计要求。本文给出的算法与文献 [2] 以及文献 [3] 中的算法不同，文献 [2] 中的 Dijkstra 算法只能求出总屏蔽系数和最小的 (V^₁,V^_n) 路径，而在实际问题中往往需要找出总屏蔽系数小于某规定值的所有 (V^₁,V^_n) 路径；文献和本文提出的算法都能够找出总屏蔽系数小于某规定值 K 的所有 (V^₁,V^_n) 路径，但文献 [3] 运用 MPS 算法找出所有总屏蔽系数和不满足要求的路径，而 MPS 算法执行时，首先要求给出电磁屏蔽拓扑图中最小数 T₁ⁿ ，求最小数T₁ⁿ 并非易事。通过修改第 k 最短路算法得到本文算法的时间复杂度为 O(n³) ，是快速寻找路径的另一种算法。

3 结 论

    本文建立了多层电磁屏蔽拓扑图模型，并将求第k最短路的算法与多层电磁屏蔽拓扑图模型相结合，提出了一种适用于多层电磁屏蔽分析的算法。利用该算法，可以找出在不同频率点下从源点到终点总屏蔽系数不符合要求的所有路径，这为改进多层电磁屏蔽条件下电子系统之间的耦合提供了另一种方法。通过本文给出的多层电磁屏蔽拓扑图模型以及相应的算法，可以找出所有的总屏蔽系数不满足要求的路径。但是电子系统十分复杂，几乎每个器件和器件之间都存在耦合，在多层电磁屏蔽条件下确定各器件间的屏蔽系数是十分困难的，所以本文采用的是假设数据，如何确定多层电磁屏蔽条件下各器件间的屏蔽系数需要进一步研究。