CDMA中基于卡尔曼滤波的盲自适应多用户检测算法

摘要　CDMA系统存在很强的多址干扰，且实际无线环境一般为多径信道。文章介绍了基于卡尔曼滤波的、且适用于多径信道的盲自适应多用户检测算法，并与基于LMS、RLS滤波的自适应多用户检测算法进行了比较。

在DS/CDMA通信系统中，为了解调出用户的有用信息，必须尽可能地抑制由其它用户扩频信号产生的多址干扰（MAI，Multiple Access Interference）[1]。尽管最佳多用户检测器可以很好地抑制MAI，但其运算量会随着用户数的增加而呈指数增加。盲多用户检测技术[2]可以在不知道其他用户信息的情况下检测出目标用户，所以在实际应用中有着十分重要的应用前景。

多用户检测作为CDMA系统重要的抗多址干扰环节，采用传统LMS、RLS滤波算法的多用户检测算法必然面临抗干扰性和收敛性的问题[3]。因此，文章将卡尔曼自适应滤波应用到多用户检测中，提出一种基于卡尔曼滤波的多用户检测算法。此算法具有良好的抗干扰性和收敛性，是一种性能较好的多用户检测算法。

1、系统模型

实际信道环境一般为多径，假设在用户数目为K的DS-CDMA系统中，接收的等效基带信号为：

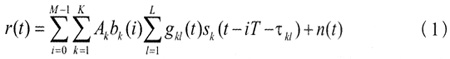
其中，M为每个用户发射的比特总数；Ak为第k个用户的幅度值；bk(i)∈{-1，+1}为第k个用户的信息比特；L为可分离的有效路径总数；Tc是码片周期；gkι(t)，τkι分别是第k个用户第条路径的信道衰落（零均值复高斯白噪声过程）和传输时延；sk(t)是第k个用户的归一化特征波形；T为比特周期；n(t)是方差为σ2的零均值加性复高斯白噪声。

接收信号通过码片匹配滤波器后，按码片速率采样得到一个维向量为：

其中，N(i)是高斯白噪声向量；I(i)由多径干扰和多址干扰信号组成。

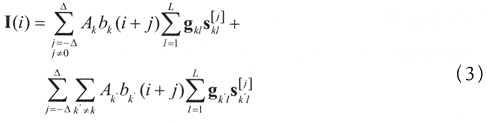
其中，△是任何用户信号多径扩展所能达到的最大比特间隔数，是一个正整数，即τkι≤△Tc。上式右边第一项代表因多径扩展而由指定用户前后比特引起的多径干扰，第二项是其他用户引起的多址干扰；Skι[j]是第k’个用户延

特征波形及信道参数唯一确定。 

2、多用户检测算法

该部分主要针对多径条件下的DS-CDMA系统，介绍了一种基于卡尔曼滤波器的盲自适应多用户检测算法。

2.1　系统建模

假设第k用户为目标用户，对应于第k个用户第条路径，×1维线性滤波器Wkι用于从接收信号中提取第k个用户第条路径的信号。用Wk=[Wkι,…,Wkι,…,WkL]表示第k个用户的滤波器组，为xL阶矩阵，则基于最小平均输出能量（MOE）的代价函数等价于如下形式：

解上述方程可得：Wkapt=R-1Sk(SKTR-1Sk)-1

其中，R=E(r(i)rH(i))，I为L×L维单位阵。

可见，用于抑制MAI的Wkapt只与目标用户的特征波形有关。第k个用户的L个线性滤波器的输出可用L×1维矢量表示为：

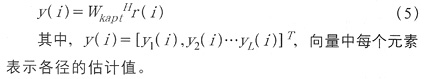
为了便于自适应实现，将上式转化为无约束优化问题。定义Sk上的投影矩阵为Ps=Sk(SHkSk)-1，将Wk的最优解分解成两个正交分量：

2.2　最优化方案分析

上述最优化问题的求解需要自适应地调整Wka的取值，使代价函数的取值达到最小，从而使判决结果达到所需的最佳性能标准。基于不同的性能指标和不同的优化算法，形成了各种多用户检测算法，如LMS滤波、RLS滤波、卡尔曼滤波。

一般来说，基于LMS滤波的多用户检测器收敛速度慢，跟踪能力不够理想；基于RLS滤波的多用户检测器计算复杂度高，不利于实时处理。相对于这两种算法，卡尔曼滤波器[4]是建立在一般的动态系统之上的，其算法实时性好，收敛速度快，跟踪性能强，抑制干扰特性好，数值稳定性高，而且不需要很大的计算量和存储量，适合在微处理器上实现。下面介绍基于卡尔曼滤波的盲自适应多用户检测器。

2.3　卡尔曼滤波器实现多用户检测

首先按照卡尔曼滤波器的模型将系统动态地表示。对于第条径，滤波器处理的动态模型为：

当系统趋于稳态时，Wkapt只与目标用户的特征波形有关，收敛于常数，其自适应分量也相应如此，所以，对第条径来说，有

（9）式为状态向量的转移等式，状态转移矩阵为单位阵I，过程噪声向量衡为零。

根据（8）和（9）可以构建出动态模型，用卡尔曼滤波器对Xι(i)，=1，…，L进行跟踪：

（1）初始化阶段，Kι（，0）=I。

（2）信号跟踪阶段，迭代计算i=1，2，3…。

Vk中各元素可以取全1，表示各径等增益合并；也可以按各径能量的大小，对判决信号进行加权。

3、卡尔曼滤波器性能分析

3.1　运算量分析

经过（6）式中的系统建模后，待估计的状态向量简化为L个（-L）×1维列向量Wιa(i)，=1，…，L。这L个列向量可以由完全相同的卡尔曼滤波器并行实现。在对每一条径进行估计的时候，列向量的维数（-L）×1维）要小于在单径信道中要估计的维数（通常是×1维），在一定程度上减小了系统复杂度。

3.2　收敛性能分析

对用卡尔曼滤波器独立处理的各条路径进行分析。对第条路径而言，由（10）和（11）式推导可得出：

上式等价为：

这就是基于卡尔曼滤波的盲自适应多用户检测的收敛性，由此可看出，MOEι(i)随迭代次数i的增加而快速趋于最小平均输出能量ξmin。即基于卡尔曼滤波的盲自适应多用户检测的收敛速率非常快，且与向量的维数(-L)有关；一般来说，(-L)为常数，在信道参数不同的情况下具有稳定的收敛速率，与用户个数无关。而随机梯度（RLS和LMS）算法的收敛速率取决于λmax/λmin，λmax和λmin分别是观测信号相关矩阵的最大特征值和最小特征值。由于观测信号相关矩阵与用户个数和干扰用户的能量有关，所以当用户个数较大和干扰用户具有较大的能量时，随机梯度算法收敛性变差。

渐近剩余能量，而基于卡尔曼滤波的盲自适应多用户检测器，有ξex=ξmin。然而，用户数固定的信噪比基于随机梯度算法的多用户检测器，渐近剩余能量通常比ξmin大。卡尔曼滤波器是状态向量的线性最小方差估计器，因此，基于卡尔曼滤波的盲自适应多用户检测器是一种线性最小方差检测器，其收敛和跟踪性能好。

4、仿真结果

设用户数目为10，目标用户为第一个用户；特性波形为31位的Gold序列；各个用户的路径数为3；多径能量采用等增益的方式进行合并，即Vk=[1，…，]L×1。

比较两种场景下，基于卡尔曼滤波，LMS算法和RLS算法的动态收敛性，稳态性能和对远近效应的抑制能力。

场景1为静态收敛性的比较。设用户1的信噪比为SNR1=10dB，干扰用户2～10的信噪比为SNR2-10=20dB，即存在很强的多址干扰。图1为三种算法在场景1下的性能比较，横坐标为迭代次数，纵坐标为滤波器的输出能量。

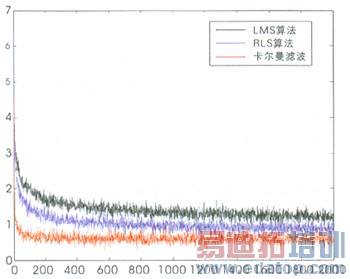
图1　静态跟踪性能

场景2为动态收敛性的比较。其中，SNR1=10dB，SNR2-8=20dB，SNR9-10=30dB。存在很强的多址干扰。开始系统中有9个用户（1-9）；迭代到700时，增加用户10，迭代到1400次时，撤走用户10。图2为三种算法在场景2下的性能比较。

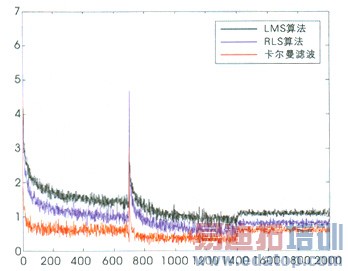
图2　动态跟踪性能

在场景3中，干扰用户的信噪比SNR2-10=20dB保持不变；目标用户SNR1从0变化到18dB。图3为三种算法在场景3下用户1信噪比和误码率关系曲线。

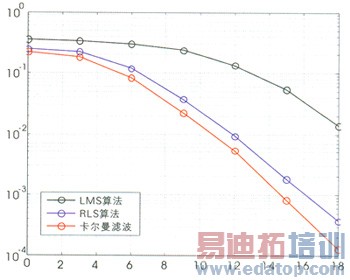
图3　稳态性能

场景4为系统抗"远-近"效应性能的比较。目标用户的SNR1=15dB，保持不变，干扰用户的SNR2-10从15dB变化到30dB，即存在很强的"远-近"效应和多址干扰。图4为三种算法在场景3下性能曲线，横坐标为干扰用户的信噪比。

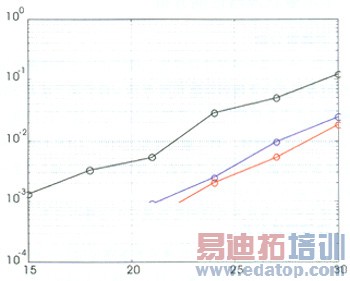
图4　抗远近效应能力

从以上场景仿真结果可看出，卡尔曼滤波的收敛、跟踪性能、抗远近效应的能力，都要优于其他两种滤波算法。

5、结束语

将卡尔曼自适应滤波用于CDMA系统的多用户检测算法中，提出了一种基于卡尔曼滤波的盲自适应多用户检测算法，在静态环境和动态环境中进行了仿真。仿真结果表明该算法抗多址干扰的能力较强，收敛速度较快，稳定性较好，具有较大的工程应用价值。

参考文献

【1】　张贤达，保铮.通信信号处理[M].北京：国防工业出版社，2000.

【2】　Zhang Xianda.Blind Adaptive Multi-user Detection Based on Kalman Filtering[J].IEEE Trans on Signal Processing，2002，50（1）：87-95.

【3】　Lim T J，Ma Y.The Kalman Filter as the Optimum Linear Minimum Squared Error Multi-user CDMA Detector [J].IEEE Trans Information Theory，2000，46（7）：2561-2566.

【4】 Hon Igm，Madhow U，Verdu S.Blind Adaptive Multi-user Detection [J].IEEE Trans Information Theory，1995，41（4）：944-960.