基于OFDM系统降低峰均功率比的研究

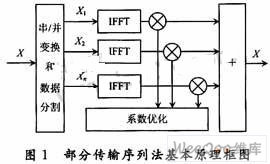
3部分传输序列(PTS)方法原理

PTS方法的基本原理如图1所示，其中，输入的数据符号被分为若干组，然后再合并这些分组，通过选择适当的分割方法和适当地改变相位以选择最优的序列，从而实现提高系统性能和降低系统的复杂度。

4一种基于相位调整的PTS搜索算法

PTS算法的关键是计算最优的旋转向量b=6[bn(1)，…，bn(v)]，通常采用穷尽搜索的方法。需要做Wv-1次循环比较。特别是当V较大时，计算的复杂度将呈指数上升。对于比较大的子载波数目(V>8)，计算的负担使得全局搜索难以实现。已经有一些方法减少系数搜索的复杂度。一些文献提出一种迭代方法，减少了搜索次数得到相位因子的一个次最优集合，就是将输人的数据块分成V束，IFFT变换之后得到V个N点的部分序列。首先假定所有部分序列的因子都相同b(v)=1，并计算合成信号的峰均比然后改变第一个因子b(1)的符号，重新计算新合成信号的峰均比。如果新的峰均比比上一步的低，则保留b(1)作为最终因子序列的部分，否则将b(1)变回前面的值。以相同的方式继续这个过程，直到所有V个因子都经历了符号翻转的尝试。和全局搜索比较，迭代方法有一点性能损失。也有一些文献提出了一些新的算法，把相位固定的几个特殊值上，比如说1，j，这样可将搜索降低到。然而当v很大时，这种算法的计算量还是很大。下面介绍一种基于相位调整的简单算法。基本的思想是用相位的增量寻找PAPR的最小值，相位可用以下公式表示：

可以很明显地看出，当k较大时，搜索的精度比较高，然而计算量也会同时增大。经过k次循环后，对应的较小的PAPR值才能得到。还可以设一个门限值来减少计算复杂度，当小于门限值时，相位调整中止，否则一直到循环结束。为了验证OFDM系统基于相位调整算法降低PAPR的有效性，考虑3种情况下的CCDF特性。在仿真中，采用128个子载波、QPSK调制的OFDM系统，PTS算法中用的V=4个子频域向量。算法使用的过采样倍数L=4。图2分别给出在不同相位优化算法下的PAPR改善性能。显而易见，基于相位调整的PTS搜索算法比穷尽搜索相当大程度上减小计算复杂度，而其性能却与穷尽搜索差不多。

5结语

通过对基于相位优化的PTS算法研究，指出以前相位优化算法中存在大量计算，提出一种基于相位增量的相位优化快速算法。分析和仿真结果表明，新算法不但能够较大程度地减小运算复杂度，而且获得了较好的峰均比，而且特别适用于过采样处理，有利于工程实现。