正交频分复用技术及其应用

在接收端，可通过下式解调出Xm,l

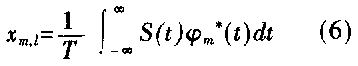
这就是OFDM的基本原理。当传输信道中出现多径传播时，在接收副载波间的正交性将被破坏，使得每个副载波上的前后传输符号间以及各副载波之间发生相互干扰。为解决这个问题，就在每个OFDM传输信号前插入一保护间隔，它是由OFDM信号进行周期扩展而来。只要多径时延不超过保护间隔，副载波间的正交性就不会被破坏。

3 OFDM系统的实现

由上面的分析知，为了实现OFDM，需要利用一组正交的信号作为副载波。典型的正交信号是{1,cosΩt,cos2Ωt,…，cosmΩt,…，sinΩt,sin2Ωt，sinmΩt,…}。如果用这样一组正交信号作为副载波，以码元周期为T的不归零方波作为基带码型，调制后经无线信道发送出去。在接收端也是由这样一组正交信号在[0,T]内分别与发送信号进行相关运算实现解调，则中以恢复出原始信号。OFDM调制解调基本原理见图2、图3所示。

在调制端，要发送的串行二进制数据经过数据编码器（如16QAM）形成了M个复数序列，这里D（m）=A（m）-jB(m)。此复数序列经串并变换器变换后得到码元周期为T的M路并行码（一帧），码型选用不归零方波。用这M路并行码调制M个副载波来实现频分复用。所得到的波形可由下式表示：

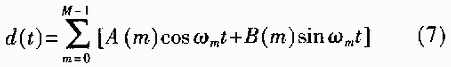
式中：ωm=2πfm，fm=f0+mΔf，Δf=1/T为各副载波间的频率间隔；f0为1/T的整倍数。

在接收端，对d(t)用频率为fm的正弦或余弦信号在[0,T]内进行相关运算即可得到A（m）、B(m)，然后经并串变抵达和数据解码后复原与发送端相同的数据序列。

这种早期的实现方法所需设备非常复杂，当M很大时，需设置大量的正弦波发生器，滤波器、调制器及相关的解调器等设备，系统非常昂贵。

为了降低OFDM系统的复杂度和成本，人们考虑利用离散傅立叶变换（DFT）及其反变换（IDFT）来实现上述功能。上面（7）式可改写成如下形式：

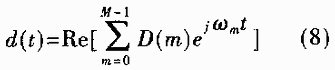
如对d(t)以fs=N/T=1/(Δt)(N为大于或等于M的正整数，其物理意义为信道数，在这里N=M)的抽样速率进行采样（满足fs>2fmax,fmax为d(t)的频谱的最高频率，可防止频率混叠），则在主值区间t=[0,T]内可得到N点离散序d(n)，其中n=0,1,…，N-1。抽样时刻为t=nΔt,则：

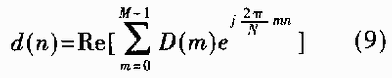
可以看出，上式正好是D（m）的离散傅立叶逆变换（IDFT）的实部，即：

d(n)=Re[IDFT[D(m)]]　　(10)

这说明，如果在发送端对D（m）做IDFT，将结果经信道发送至接收端，然后对接收到的信号再做DFT，取其实路，则可以不失真地恢复出原始信号D（m）。这样就可以用离散傅立变换来实现OFDM信号的调制与解调，其实现框图如图4所示。

用DFT及IDFT来实现OFDM系统，大大降低了系统的复杂度，减小了系统成本，为OFDM的广泛应用奠定了基础。

4 OFDM实现方式的计算机仿真

由上节可知，要实现OFDM，可以采用传统的多路正交副载波调制的方式，也可以采用傅立叶变换的方式，这两种方式所组成的系统复杂度和成本有很大差别。目前实用的OFDM系统均采用了傅立叶变换的实现方式，该方式与传统方式相比，大大简化了系统的构成，降低了成本。这里用计算机仿真方法对两种方式进行模拟，进一步说明两种方式具有相同的系统效果。

仿真系统用Matlab来实现，源数据采用一波形文件，采样后共有680个串行数据，将其分为34帧，每帧的20个数据分别构成10路进行码的实部和虚部。

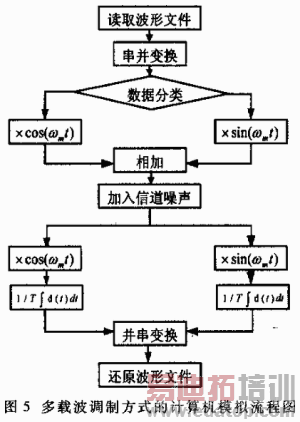
在多路正交副载波调制方式中，用20个正交的三角波对10路码分别进行调制，将结果相加作为已调波。在接收端再用这20个三角波对接收波进行相关解调，将解调数据与源数据进行比较。程序流程图见图5。

在傅立叶变换方式中，使用快速傅立叶算法，直接对每帧数据进行IFFT，得到已调序列。在接收端对接收到的序列进行FFT，还原出原始数据。程序流程图如图6所示。

为了模拟无线通信环境，在信道中加入低幅度的高斯噪声。图7为源数据波形与通过两种方式得到的OFDM输出波形。可以看出，两种方式获得了相同的系统效果。

5 OFDM系统在宽带通信中的应用

（1）数字声广播工程（DAB）

欧洲的数字声广播工程（DAB）--DABEUREKA147计划已成功地使用了OFDM技术。为了克服多个基站可能产生的重声现象，人们在OFDM信号前增加了一定的保护时隙，有效地解决了基站间的同频干扰，实现了单频网广播，大大减少整个广播占用的频带宽度。

来源：21IC电子网