基于RSSI的室内无线网络定位技术研究

把该范围内的RSSI值全部取出，再求几何平均值，即可得到最终的RSSI值。

在d=1 m处，采集50组RSSI值，进行高斯滤波处理。

如图3所示，滤波前RSSI波动比较大，滤波后比较平滑。滤波前|RSSI|的平均值为38．9，计算距离d=O．71 m；滤波后|RSSI|的平均值为39．42，计算距离d=O．81 m。显然，高斯滤波能很好地提高测距精度。

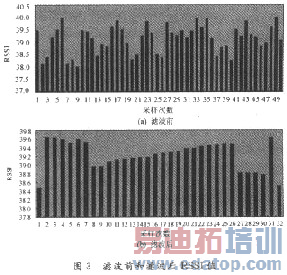
3 定位算法

假设无线定位网络中有N个已知位置的参考节点，坐标为(x1，y1)，(x2，y2)，…，(xN，yN)，RSSI测量值为(RSSI1，RSSI2，…，RSSIN)。通过利用无线信号传播衰落模型计算得到待定位节点到四个已知位置的参考节点的距离为R1，R2，…，RN，则可以得到以下方程：

最终定位算法的研究就是求解该方程。在求解(x，y)过程中，选用基于泰勒级数展开迭代法进行计算。选用泰勒级数的原因基于以下几个方面：

(1)无需提供测距差测量值误差的先验信息。
    (2)可以应用于两个以上数目距离差测量的定位估计。
    (3)对距离差统计没有特殊要求。
    (4)在适当的距离差噪声水平上提供较准确的定位估计。

使用泰勒级数进行定位计算，首先面临的一个问题即泰勒级数展开需要一个与实际位置差距不大的初始值，初始值的选择越接近真实值，越可以保证算法的收敛性以及实时性。本文采用极大似然估计法来获取初始值，求得初始值公式为：

式中：

根据取得的值作为Taylor级数展开的循环初值，然后用Taylor级数展开，进行矩阵计算，并反复迭代求精，直到误差满足预先设定的门限，得出最终的位置坐标。

式中：

作者：朱明辉 张会清   来源：现代电子技术