- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
基于信息熵的Markov网络结构学习算法研究
录入：edatop.com 点击：
1 引言
日常生活中人们常需要处理不确定信息，例如：预测明天是否会下雨，病人是否得了某种疾病。Bayesian网是进行不确定性推理的有力工具，被广泛应用于人工智能、专家系统、数据挖掘等领域，是当前研究的热点。利用Bayesian网可以推理不确定性知识，从而达到较好效果。
Markov网是类似于Bayesian网的另一种进行不确定性推理的有力工具。Markov网是一个无向图，构造时无需发现边的方向，要比构造Bayesian网容易得多。首先构造Markov网，再求出与之等价的Bayesian网。本文提出一种基于信息熵的方法构造Markov网，给出一个有效的基于信息独立测试的Markov网的构造算法，该算法是一种基于依赖分析的算法。在测试样本中的条件独立时，利用信息论中验证信息独立的一个重要结论，从而大大提高效率。为衡量构造的Markov网的好坏，引入I-图、D-图和P-图的概念。
2 依赖模型与MarkOV网
知识可以用一组条件独立和条件概率表示，Markov网(无向图)用于表示条件独立。下面主要讨论如何用Markov网表示一个依赖模型M(一组条件独立的集合)以及如何衡量Markov网的好坏(引入I-图、D-图和最小P-图)。
定义1：依赖模型M定义为一组条件独立的集合，设X，Y，Z是全集U的3个不相交的子集，M={I(X，Z，y)}。其中的I(X，Z，y)表示在给定Z的条件下，X独立于Y，即：p(X|Y，Z)=p(X|Z)和p(Y|X，Z)=p(Y|Z)。
定理1：依赖模型M中的I(X，Z，y)满足以下4个性质，设X，Y，Z是全集U的3个不相交的子集，
(1)对称性：I(X，Z，Y)XXXXXXI(Y，Z，X)；
(2)分解律：I(X，Z，Y∪W)=》I(X，Z，Y)＆I(X，Z，W)；
(3)弱归并律：I(X，Z，Y∪W)→I(X，Z，∪W，Y)；
(4)减缩律：I(X，Z，y)&I(X，Z，∪Y，W)→I(X，Z，Y∪W)若联合概率函数p严格为正，Vx，p(x)>0，则相交律成立。
(5)相交律：I(X，Z，∪W，Y)＆I(X，Z，∪Y，W)→I(X，Z，Y∪W)给定一个依赖模型M，利用无向图中节点分割的概念表示依赖模型中的条件独立。
定义2：在有向无环图G中，X，Y，Z是U上3个不相交的子集，删去节点集Z及其相应的边，使节点集X，Y之间再无边相连，称Z将X，Y分割开，记为<X|Z|Y>G。用<X|Z|Y>G表示依赖模型中条件独立信息I(X，Z，Y)，得到一个依赖模型的图形化表示方式，继续用I-图、P-图、D-图的概念衡量依赖模型M中的所有条件独立信息和最优Markov网。
定义3：设M为依赖模型，I(X，y，Z)M表示依赖模型M所蕴含的依赖关系(条件独立)I(X，y，Z)。无向图G=(V，E)为M的I-图、D-图、P-图，定义如下：
(1)G是M的I-图(独立图)，当<X|Z|Y>G=<X|Z|Y>M。
(2)G是M的D-图(依赖图)，当<X|Z|Y>M=><X|Z|Y>G。
(3)G是M的P-图(理想图)，当<X|Z|Y>M<=<<X|Z|Y>G。
由上述定义可知，I-图不一定包含依赖模型M所蕴含的所有依赖关系，但I-图中蕴含的依赖关系M中一定蕴含；D-图恰好相反，D-图包含依赖模型M所蕴含的所有依赖关系，但D-图中蕴含的依赖关系M中不一定蕴含；P-图是最理想的情况，P-图与M形成一一对应关系。空图(不含任何边的无向图)是一个平凡的D-图，而完全图(包含所有边的无向图)是一个平凡的I-图。
定义4：设一个无向图G是M的一个I-图，若删除G中任何一条边后，使得G不再是M的I-图，则称G为M的最小I-图。显然，最小I-图能够最多地表示依赖模型M中的依赖关系。
定理2：满足对称性、分解性、相交律和弱归并律的依赖模型M,从完全图中删除所有条件独立性成立的边，则产生一个唯一的最小I-图。
3 信息熵概述
Markov网结构用来消除不确定性的东西，信息的载体称为消息。含有信息的消息集合称为信源。信源的信息熵，就是信源提供整个信息的总体度量。所以如果消息消除的不确定性越大，信源的信息熵就越小，信息间的相互依赖性就越大；反之，信息间的相互独立性就越大。具体概念作如下定义：
定义5：设属性X具有r种可能状态，Pi为状态Xi时的概率，则信息熵可定义为：
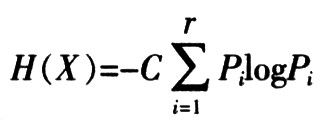
式中，C为大于0的常数。
定义6：设X，Y为两个相互关联的随机变量，称：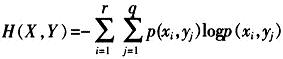
为X，Y的联合熵。H(X|Y)=H(X，i=1j=1Y)-H(Y)为给定Y时X的条件熵。条件熵H(X|Y)表示在观测到Y的结果后，对X保留的不确定性度量。
定义7：设X，Y，Z为3个不相交的变量集，称：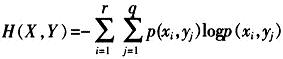
的互信息。
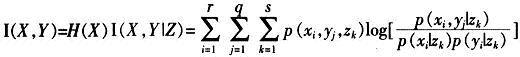为给定Z的条件下，X和Y的互信息(条件互信息)。
定理3：互信息I(X，Y)和I(X，Y|Z)具有如下性质：
(1)对称性，即I(X，Y)=I(Y，X|Z)和I(X，Y|Z)=I(Y，X|Z)；
(2)非负性，即I(X，Y)≥0和I(X，Y｜Z)≥0。而且，当且仅当X和Y条件独立时有I(X，Y)=0。同理，当且仅当在给定条件Z，X和Y条件独立时I(X，Y｜Z)=0。
4 基于信息熵的Markov网构造算法
给定一样本集(n个属性的一张二维表)，先对系统中N个变量构建一个完全无向图氏，然后利用信息独立测试理论有效删剪PG图，以得到所求的Markov网。
首先给出这个算法所需要的一些假设：给定的样本数据集D是完整的；所有的变量取值均为离散性，若取值连续可先进行离散化。
第1步：构造完全有向图
定义8：设一个系统含有N个变量｛X1，X2，……，Xn}，完全有向图PG={<Xi,Xj>|，其中i,j=1，2，…，n且i≠j，<Xi，Xj>表示Xi与Xj有因果关系Xi→Xj}。由此定义可知，PG是一个I-图。
日常生活中人们常需要处理不确定信息，例如：预测明天是否会下雨，病人是否得了某种疾病。Bayesian网是进行不确定性推理的有力工具，被广泛应用于人工智能、专家系统、数据挖掘等领域，是当前研究的热点。利用Bayesian网可以推理不确定性知识，从而达到较好效果。
Markov网是类似于Bayesian网的另一种进行不确定性推理的有力工具。Markov网是一个无向图，构造时无需发现边的方向，要比构造Bayesian网容易得多。首先构造Markov网，再求出与之等价的Bayesian网。本文提出一种基于信息熵的方法构造Markov网，给出一个有效的基于信息独立测试的Markov网的构造算法，该算法是一种基于依赖分析的算法。在测试样本中的条件独立时，利用信息论中验证信息独立的一个重要结论，从而大大提高效率。为衡量构造的Markov网的好坏，引入I-图、D-图和P-图的概念。
2 依赖模型与MarkOV网
知识可以用一组条件独立和条件概率表示，Markov网(无向图)用于表示条件独立。下面主要讨论如何用Markov网表示一个依赖模型M(一组条件独立的集合)以及如何衡量Markov网的好坏(引入I-图、D-图和最小P-图)。
定义1：依赖模型M定义为一组条件独立的集合，设X，Y，Z是全集U的3个不相交的子集，M={I(X，Z，y)}。其中的I(X，Z，y)表示在给定Z的条件下，X独立于Y，即：p(X|Y，Z)=p(X|Z)和p(Y|X，Z)=p(Y|Z)。
定理1：依赖模型M中的I(X，Z，y)满足以下4个性质，设X，Y，Z是全集U的3个不相交的子集，
(1)对称性：I(X，Z，Y)XXXXXXI(Y，Z，X)；
(2)分解律：I(X，Z，Y∪W)=》I(X，Z，Y)＆I(X，Z，W)；
(3)弱归并律：I(X，Z，Y∪W)→I(X，Z，∪W，Y)；
(4)减缩律：I(X，Z，y)&I(X，Z，∪Y，W)→I(X，Z，Y∪W)若联合概率函数p严格为正，Vx，p(x)>0，则相交律成立。
(5)相交律：I(X，Z，∪W，Y)＆I(X，Z，∪Y，W)→I(X，Z，Y∪W)给定一个依赖模型M，利用无向图中节点分割的概念表示依赖模型中的条件独立。
定义2：在有向无环图G中，X，Y，Z是U上3个不相交的子集，删去节点集Z及其相应的边，使节点集X，Y之间再无边相连，称Z将X，Y分割开，记为<X|Z|Y>G。用<X|Z|Y>G表示依赖模型中条件独立信息I(X，Z，Y)，得到一个依赖模型的图形化表示方式，继续用I-图、P-图、D-图的概念衡量依赖模型M中的所有条件独立信息和最优Markov网。
定义3：设M为依赖模型，I(X，y，Z)M表示依赖模型M所蕴含的依赖关系(条件独立)I(X，y，Z)。无向图G=(V，E)为M的I-图、D-图、P-图，定义如下：
(1)G是M的I-图(独立图)，当<X|Z|Y>G=<X|Z|Y>M。
(2)G是M的D-图(依赖图)，当<X|Z|Y>M=><X|Z|Y>G。
(3)G是M的P-图(理想图)，当<X|Z|Y>M<=<<X|Z|Y>G。
由上述定义可知，I-图不一定包含依赖模型M所蕴含的所有依赖关系，但I-图中蕴含的依赖关系M中一定蕴含；D-图恰好相反，D-图包含依赖模型M所蕴含的所有依赖关系，但D-图中蕴含的依赖关系M中不一定蕴含；P-图是最理想的情况，P-图与M形成一一对应关系。空图(不含任何边的无向图)是一个平凡的D-图，而完全图(包含所有边的无向图)是一个平凡的I-图。
定义4：设一个无向图G是M的一个I-图，若删除G中任何一条边后，使得G不再是M的I-图，则称G为M的最小I-图。显然，最小I-图能够最多地表示依赖模型M中的依赖关系。
定理2：满足对称性、分解性、相交律和弱归并律的依赖模型M,从完全图中删除所有条件独立性成立的边，则产生一个唯一的最小I-图。
3 信息熵概述
Markov网结构用来消除不确定性的东西，信息的载体称为消息。含有信息的消息集合称为信源。信源的信息熵，就是信源提供整个信息的总体度量。所以如果消息消除的不确定性越大，信源的信息熵就越小，信息间的相互依赖性就越大；反之，信息间的相互独立性就越大。具体概念作如下定义：
定义5：设属性X具有r种可能状态，Pi为状态Xi时的概率，则信息熵可定义为：
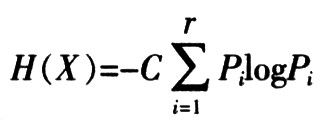
式中，C为大于0的常数。
定义6：设X，Y为两个相互关联的随机变量，称：
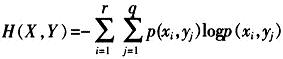为X，Y的联合熵。H(X|Y)=H(X，i=1j=1Y)-H(Y)为给定Y时X的条件熵。条件熵H(X|Y)表示在观测到Y的结果后，对X保留的不确定性度量。 定义7：设X，Y，Z为3个不相交的变量集，称：
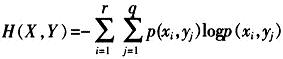的互信息。 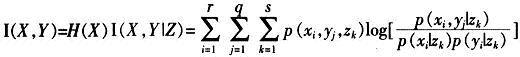为给定Z的条件下，X和Y的互信息(条件互信息)。 定理3：互信息I(X，Y)和I(X，Y|Z)具有如下性质：
(1)对称性，即I(X，Y)=I(Y，X|Z)和I(X，Y|Z)=I(Y，X|Z)；
(2)非负性，即I(X，Y)≥0和I(X，Y｜Z)≥0。而且，当且仅当X和Y条件独立时有I(X，Y)=0。同理，当且仅当在给定条件Z，X和Y条件独立时I(X，Y｜Z)=0。
4 基于信息熵的Markov网构造算法
给定一样本集(n个属性的一张二维表)，先对系统中N个变量构建一个完全无向图氏，然后利用信息独立测试理论有效删剪PG图，以得到所求的Markov网。
首先给出这个算法所需要的一些假设：给定的样本数据集D是完整的；所有的变量取值均为离散性，若取值连续可先进行离散化。
第1步：构造完全有向图
定义8：设一个系统含有N个变量｛X1，X2，……，Xn}，完全有向图PG={<Xi,Xj>|，其中i,j=1，2，…，n且i≠j，<Xi，Xj>表示Xi与Xj有因果关系Xi→Xj}。由此定义可知，PG是一个I-图。
上一篇：控制端口流量
不让交换机被“顶死”
下一篇：基于华为路由器接入的解决方案
