- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
神经网络预测编码器的设计及应用
录入:edatop.com 点击:
1 BP网络结构及其算法
反向传播算法又称误差后向传播算法(Error Back Propagation Algorithm),它是用来训练多层前馈网络的一种学习算法。是一种有监督的学习算法。通常称用误差反向传播算法训练的网络叫BP网络。
如图1所示,该BP网络具有一个输入层,两个隐含层(也称中间层)和一个输出层组成,各层之间实行全连接。
BP神经网络的隐含层通常具有多个,其传输函数常常采用sigmoid函数,而输入输出层则采用线性传输函数。
2.1 预测器层数
kolmogorov定理(即映射网络存在定理),一个隐含层的网络,如果隐含层的功能函数是连续函数,则网络输出可以逼近一个连续函数。具体的说,设网络有p个输入,q个输出,则其作用可以看作是由p维欧式空间到q维欧式空间的一个非线性映射。
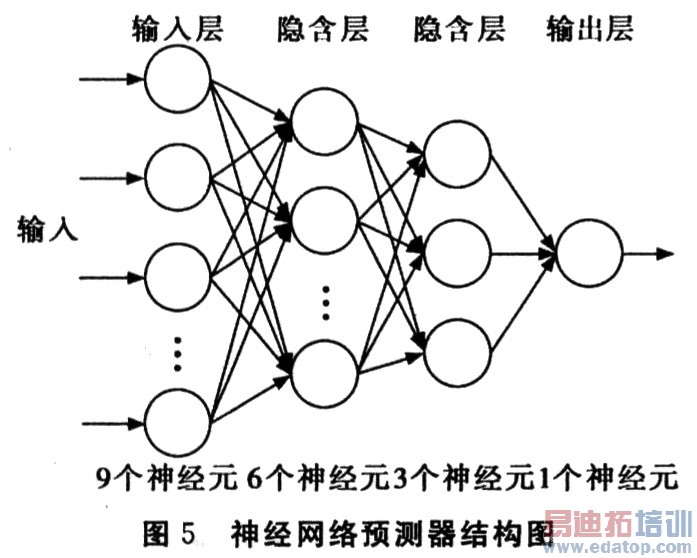
Kolmogorov定理表明含一个隐含层的BP前馈网络是一种通用的函数逼近器,为逼近一个连续函数,一个隐含层是足够的。当要学习不连续函数时,则需要两个隐含层,即隐含层数最多两层即可,Lippmann等也给出了同样的结论。通过参考以上定理、规则,并结合试验最终确定本文实现的神经网络预测器采用两个隐含层,一个输入层和一个输出层的BP网络。
2.2 节点数
网络的输入与输出节点数是由实际问题的本质决定的,与网络性能无关。而当像素间距离超过5时,像素之间的相关性就很小,并且在图像的某一个区域内,色度信息不会突变,因此,本文设计的BP神经网络预测器利用与当前像素相邻的9个像素来预测当前像素,这样不仅可以利用同一色分量内像素之间的相关性,也可以利用不同色通道之间像素的相关性进行预测。邻域像素的选择如图3所示。
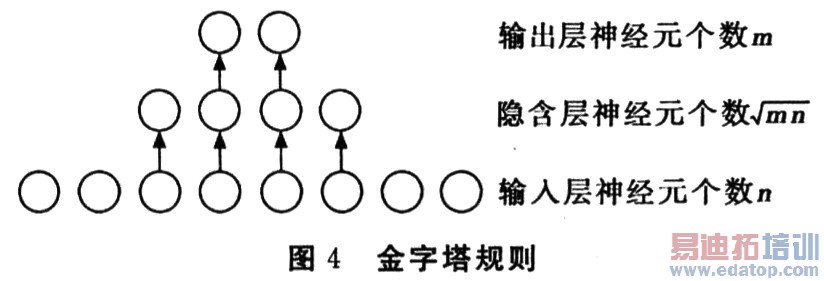
实际上,隐含层神经元数取决于训练样本数的多少、噪声量的大小及网络学习的输入一输出函数关系或分类关系的复杂程度。对许多应用场合均适用的一条有关确定隐结点数的规则即所谓的几何金字塔规则(geometric pyramidrule):从输入层到输出层,结点数不断减少,其形好似金字塔,如图4所示。
反向传播算法又称误差后向传播算法(Error Back Propagation Algorithm),它是用来训练多层前馈网络的一种学习算法。是一种有监督的学习算法。通常称用误差反向传播算法训练的网络叫BP网络。
如图1所示,该BP网络具有一个输入层,两个隐含层(也称中间层)和一个输出层组成,各层之间实行全连接。
BP神经网络的隐含层通常具有多个,其传输函数常常采用sigmoid函数,而输入输出层则采用线性传输函数。


2.1 预测器层数
kolmogorov定理(即映射网络存在定理),一个隐含层的网络,如果隐含层的功能函数是连续函数,则网络输出可以逼近一个连续函数。具体的说,设网络有p个输入,q个输出,则其作用可以看作是由p维欧式空间到q维欧式空间的一个非线性映射。
Kolmogorov定理表明含一个隐含层的BP前馈网络是一种通用的函数逼近器,为逼近一个连续函数,一个隐含层是足够的。当要学习不连续函数时,则需要两个隐含层,即隐含层数最多两层即可,Lippmann等也给出了同样的结论。通过参考以上定理、规则,并结合试验最终确定本文实现的神经网络预测器采用两个隐含层,一个输入层和一个输出层的BP网络。
2.2 节点数
网络的输入与输出节点数是由实际问题的本质决定的,与网络性能无关。而当像素间距离超过5时,像素之间的相关性就很小,并且在图像的某一个区域内,色度信息不会突变,因此,本文设计的BP神经网络预测器利用与当前像素相邻的9个像素来预测当前像素,这样不仅可以利用同一色分量内像素之间的相关性,也可以利用不同色通道之间像素的相关性进行预测。邻域像素的选择如图3所示。

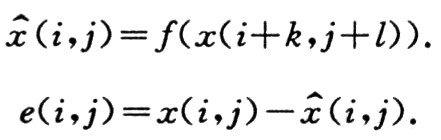
实际上,隐含层神经元数取决于训练样本数的多少、噪声量的大小及网络学习的输入一输出函数关系或分类关系的复杂程度。对许多应用场合均适用的一条有关确定隐结点数的规则即所谓的几何金字塔规则(geometric pyramidrule):从输入层到输出层,结点数不断减少,其形好似金字塔,如图4所示。
上一篇:混插刀片选半高还是全高?
下一篇:IP媒体服务器控制协议的选择


