基于同伦算法的逆变电源特定消谐法的研究

3 同伦算法的建立

3．1 同伦算法

同伦方程的数值解法有2种：同伦延拓法；参数微分法。采用参数微分法将非线性方程组(4)简写为：

F(a)=0 (5)

式中，F：D∈Rn→Rn。令a*是方程组(5)的解。

非线性超越方程组(5)，一般采用牛顿迭代法求解，但该方法对初值的选取要求较为严格，即要求初始近似解a0与解a*充分靠近，才能使迭代数{ak}收敛于a*。实际计算中要找到满足要求的迭代初始值往往很困难，如果给出的初始值导致迭代不收敛，就需要重新给初始值再计算，这样就大大降低了求解速度，难以实现实时控制。为了解决这个问题，这里尝试用同伦法求解。同伦法是一种用于非线性方程组数值求解的新方法，具有全局收敛和收敛速度快等优点，其基本的思想是：对于该方程组，引人参数t，构造一族映射H，使当t为某一特定值(例如t=1)时，H就是映象F，而当t=0时，得出方程组F0(a)=0的解a0是已知的。也就是说，构造一簇映射H：D×[O，1]∈Rn+1→Rn，代替单个映射F，使H满足条件：

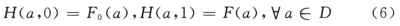
式中：F0(a)=0的解a0为已知，而方程H(a，1)=0就是原来的非线性方程组(5)，现在把问题变为求解同伦方程：

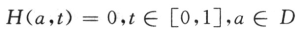
构造满足条件(6)的同伦H可以是各种各样的。这里，构造H(a，t)=F(a)+(t-1)F(a0)。可以证明，该同伦方程存在惟一解a=a(t)，且a(t)是微分方程式(7)的解，式(7)为：

因此，通过求解微分方程初值问题式(7)的数值解，可得到方程(5)的解。用具有二阶精度的中点求积法，得到：

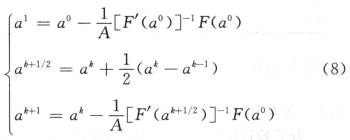
式中：k=1，2，…，A-1，A为正整数。

只要F'(a)-1存在，且A足够大，可证明由式(8)求得的nA可作为式(5)的解a*的一个好的近似，再用牛顿迭代法可求得精确解。

3．2 算例

根据文中采用的模型及算法，取开关角N=8，随着基波幅值q的变化得到一组开关角的解轨迹(取UDC=1)，如图4为显示开关角aN随基波幅值q的变化，取q=0.3，q=0.5和q=0.7时得到的三组开关角的解如表3所示。

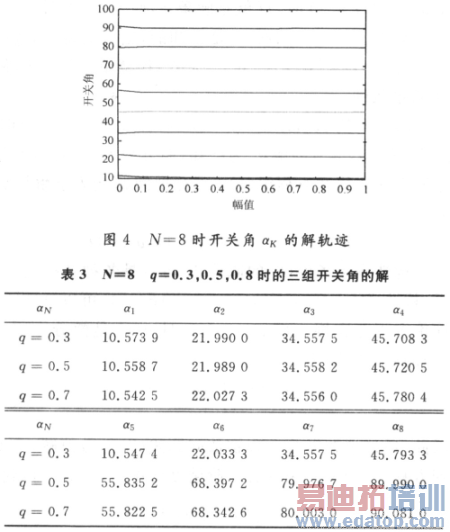
在实际的运算过程中，将牛顿法和该方法进行比较，发现这种方法的收敛域扩大，如N=8，q=O.9，取初值a0=[5，20，30，40，50，60，70，80]时，用牛顿法迭代和简化牛顿法都不收敛，用同伦法(固定迭代次数A=4)则只需7次。如N=20，q=1.0，a0=[1，8，12，15，20，25，28，30，35，40，45，50，52，60，65，68，70，75，80，90]时，用牛顿法迭代不收敛，用同伦法只需3次，加上预迭代10多次；若用同样一组靠近真值的初始值开始迭代，尽管两种方法都收敛，但同伦法的迭代次数比牛顿法少。取a0=[9，10，16，18，23，26，30，35，38，44，46，52，54，61，62，69，70，78，78.2，90]时，用两种方法都收敛，但用同伦法要比牛顿法迭代次数少很多，这样的例子很多，所以同伦法有很多优越性。

4 研究结果

4．1 仿真研究

为了验证同伦算法所得结果谐波消除的效果，采用Matlab仿真，以五电平级联多电平逆变器为例，对SHEPWM控制方法进行了仿真研究。仿真参数：调制频率50 Hz，直流电压VDc=20 V，基波幅值q=O.7，α见表3。图5给出了五电平级联多电平逆变器输出电压(V0)的仿真PWM波形和谐波频谱分析如图1所示，开关个数N=8通过Matlab仿真和DSP系统中的TMS320F2812实验台给出了结果。由图5可见，3，5，7，9…等低阶奇次谐波被消除了，由此说明，由前面的同伦算法计算得到的结果是正确的，它与预期的谐波次数一致。

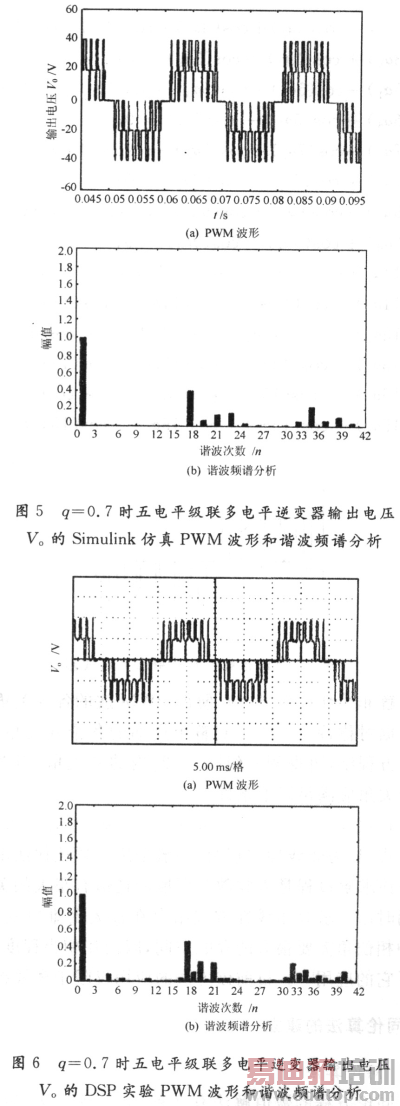
4．2 实验研究

为了进一步验证同伦算法计算的SHEPWM结果的实际消谐效果，进行具体的实验研究。以TI公司的TMS320F2812控制平台为控制器，把离线运算结果(见表3)中的相应部分存入到DSP中，然后通过查表法取得开关切换时刻。图6所示为实验波形。

对比图5与图6可知，五电平级联多电平逆变器的实验波形与仿真结果非常一致，故实验所得的波形是正确。验证的同时说明，由同伦算法计算出的SHEPWM超越方程组的结果是正确的。

5 结 语

这里通过对逆变电源消谐模型的研究，提出了用同伦算法求解该模型的方法。这种算法的优点在于它对初值没有严格的要求，并且具有很宽的收敛范围和收敛速度，可以保证求解过程的正确性和快速性。并通过仿真和实验验证了该算法。如果能提高CPU速度或采用并行运算进一步提高运行速度，实现实时消谐PWM控制是完全可能的。因此可以预见它将成为逆变器PWM控制中很有发展前景的控制算法。