- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
一种UHF无源RFID标签芯片阻抗测试方法研究
杨跃胜1,2,武岳山1,2,熊立志2,田 平2,李 曼1
射频识别RFID(Radio Frequency Identification)系统由阅读器和电子标签组成,天线是阅读器和电子标签通信的桥梁。为了使阅读器发射的射频能量最大限度地被无源标签天线所吸收,理论要求电子标签天线和标签芯片阻抗达到共轭匹配。即UHF频段无源RFID单芯片的阻抗值,直接决定着电子标签天线设计,进而影响电子标签的性能。
UHF频段无源RFID电子标签采用反射调制原理工作,其原理决定了电子标签芯片阻抗具有UHF频段、无源、时变性、非线性等复杂特性,尤其是对于尺寸不足1 mm2的单芯片,本身即存在着尺寸小、射频影响等困难,导致常规的测试方法很难准确地对电子标签芯片阻抗进行测试。本文研究了UHF无源单芯片阻抗测试方法,通过对标准芯片阻抗测试,对测试方法进行了检验。
1 测试原理
对于UHF频段无源电子标签工作特征而言,由于单芯片工作在UHF频段,通过标签芯片pad的任何引线都将产生寄生电容或者寄生电感,从而对芯片阻抗测试产生影响。同时,采用常规的测试方法,引线的长度和宽度很难把握,测试的重复性差,不利于标签芯片阻抗的准确测试。本文采用传输线阻抗匹配网络对芯片阻抗进行测试,较好地解决了实际测试中面临的接入困难等问题。
由分布参数电路理论可知,在UHF频段,传输线的宽度和长度影响着传输线特性阻抗值。例如本文所使用的平行双导线,其工作频带很宽,可用于1 GHz以下所有频率中,平行双导线的特性阻抗值[3]如式(1)所示:
![]()
式中,a为平行双导线中心的距离,b为平行双导线单根导线的宽度。
利用传输线此特性,构建一个传输线阻抗匹配网络模型,如图1所示。左端为匹配网络的前端电路,输入能量为芯片正常工作状态下的最小功耗,参考阻抗可以用一个阻抗为50 Ω的电阻R0代替。终端开路的λ/4的传输线相当于短路,实现阻抗变换,在λ/4传输线末端并联一段终端短路的短截线,此段短截线相当于一个感抗元件。芯片一般呈现容性,并联在λ/4传输线末端,通过改变短截线终端与芯片的距离Lλ,可以改变短截线引入的感抗大小,进而与芯片阻抗达到共轭匹配。当芯片与匹配网络达到共轭匹配状态时,芯片两端的回波损耗S11最小,即芯片几乎吸收了前端电路传输的所有能量,并且是正常工作的最小能量。通过观察回波损耗S11的值,用以确定最优的传输线阻抗Z0以及短截线距离芯片的长度Lλ,反推此时的阻抗网络,即可获得无源RFID标签芯片在工作状态时的输入阻抗。
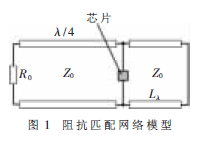
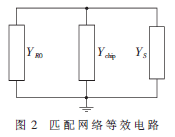
图2为阻抗匹配网络的等效电路,YR0代表电阻R0经λ/4传输线变换后的输入导纳,Ys代表末端短路的短接线在芯片连接处的输入导纳,Ychip代表芯片的输入导纳。Ychip和YR0、Ys相并联。由传输线相关理论[4]可得:

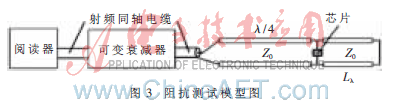
实际测试模型如图3所示,读写器和可调衰减器通过同轴线相连,其输出口参考阻抗均为50 Ω。运行读写器,将其频率设置为915 MHz,通过调节可调衰减器,减小输入阻抗匹配网络的能量,同时调节传输线阻抗Z0以及短截线终端距离芯片的距离Lλ,使芯片能够获得正常工作的最小能量。此时,将Z0和Lλ的值代入式(8)即可得到芯片在最低功耗下的阻抗值。
2 仿真分析
利用ADS仿真软件对阻抗测试模型进行仿真,标签芯片接口用Term1表示,输出阻抗可以按照芯片的标准阻抗设定,阅读器与衰减器串联之后的输出接口用Term2表示,输出阻抗为50 Ω,物理长度为λ/4的传输线模型用TL1表示,其角度为90 deg,特性阻抗为Z0。在915 MHz频点,将Term1的阻抗值用NXP_XM芯片data-
sheet所规定的阻抗值18.1-149*j代替时,得到最优阻抗Z0为250 Ω
从图4所示标准芯片的回波损耗仿真图形可以看出,标准芯片与阻抗匹配网络已经达到比较好的匹配状态,证明测试原理有效。

3 实际测试及误差分析
基于以上仿真制作测试板。结合芯片封装形式以及SMA头的宽度,选择平行双线的中心距为4.15 mm,利用式(1),计算平行双线宽度b值及对应的Z0值如表1所示,依据表1所示的计算值可以制作出测试板。为了提高测试板的抗干扰能力,SMA头接入信号后首先通过一个巴伦,将非平衡信号转换成平衡信号,然后再接到后端的平行双导线。

测试板材料将对传输线上的波长产生影响,结合传输线理论,对于终端开路的传输线而言,当0<z<λ/4时,输入阻抗呈现容性,当z=λ/4时,输入阻抗为0,相当于短路,当λ/4<z<λ/2时,输入阻抗呈现感性,其中z为传输线的长度。利用网络分析仪进行实际测试得知,该传输线上的波长为252 mm,芯片应该放在λ/4处,即距离输出端口63 mm处。
利用此测试板对工作在915 MHz的标准芯片进行测试,获得最优的Z0和Lλ值,代入公式(8)即可得到NXP_XM芯片阻抗为:17.1-j145,Impinj_Monza4芯片阻抗为:10.2-j142 Ω。而datasheet所给出的NXP_XM芯片阻抗为:18.1-j149,Impinj_Monza4单端口连接芯片阻抗为:11-j143 Ω。测试标准芯片所得阻抗值与芯片的datasheet相比略有偏差。
误差产生的原因如下:(1)任何芯片阻抗值均具有离散性,这是由芯片本身的质量所决定的,所作的测试仅仅是对标准芯片的个别测试,而datasheet所给出的结果是一定数量的芯片阻抗取其平均值所得。(2)从仿真中可以看出,短截线与芯片距离的微小偏差便会对芯片的阻抗产生影响,可以利用多次读数取平均值减小误差。(3)作为通用测试板,传输线阻抗值与芯片测试所需要的值会有偏差,但是通过计算之后发现影响不大,依然能够保证较低的回波损耗值。
本文提出一种UHF频段无源RFID标签芯片在最低功耗工作状态下的阻抗测试方法,其测试方法简单、准确性高、实际应用性强。利用该测试方法对工作在单个频点的芯片阻抗进行测试,同时通过多频点测试,可以测得一个频段内芯片的阻抗值变化情况。另外,该测试方法在测试板中引入了巴伦,提高了测试板抗干扰能力。此UHF无源单芯片阻抗测试的新方法改善了传统测试方法的不足,提高了测试的精准度,为下一步频段内阻抗测试奠定了基础。
参考文献
[1] KLAUS F.射频识别(RFID)技术[M].陈大才,译.北京:电子工业出版社,2001.
[2] MURFETT D.The challenge of testing RFID integrated circuits[J].In IEEE Int.Electron.Design,Test,Appl.Workshop,2004(6):410-412.
[3] 黄玉兰.射频电路理论与设计[M].北京:人民邮电出版社,2008.
[4] DEVENDRA K M.Radio-frequency and microwave communication circuits analysis and design,Second Edition[M].张肇义,译.北京:电子工业出版社,2005.
[5] 李云华,刘弈昌.标签芯片阻抗的在线测量[J].射频识别,2010(2).
[6] MATS L,HAWRYLAK P,MICKLE M.In-situ characterization of passive RFID tag performance at absolute minimum power levels[J].In IEEE AP-S Int.Symp.,2007(7):2741-2744.
[7] PURSULA P,SANDSTROM D,JAAKKOLA K.Backscattering-based measurement of reactive antenna input impedance[J].IEEE Trans.Antennas Prapag.,2008,56(2):469-474.


