- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
GPS相对定位在重力卫星KBR测距中的应用
地球重力场是地球的一个基本物理场,重力场及其变化反映了地球表层及其内部的物质分布和运动,决定了大地水准面的起伏和变化,地球重力场的精确测量对大地测量、地球物理、地球动力学和海洋学等学科的发展具有极其重要的意义。卫星重力测量技术的应用对于地球重力场的测量具有划时代的意义,是当今大地测量领域的研究前沿和关注热点之一。常规的重力场确定方法主要依靠地面重力观测,地面观测周期较长,且占地球四分之三的海洋重力数据缺乏,确定重力场的精度受到限制。随着空间定位技术的发展,近年来在地球重力场研究方面所取得的成就远远超出过去30年的总和。20世纪80年代出现的卫星测高技术较大地提高了重力场的确定精度,如著名的EGM96模型。2000年7月由德国GFZ发射的重力卫星GHAMP,迈出了卫星重力测量的重要一步。2002年3月由美国宇航局和欧洲联合发射的低跟踪卫星GRACE,采用KBR双向测距,同时利用双频 GPS定位、测时结果修正KBR测距,使得测距精度达到几十微米,距离变率测定精度达到0.1 μm/s。此外,欧洲空间局也在2009年3月份成功发射了GOCE重力梯度卫星,卫星重力测量得到了空前的发展。但是,我国目前对重力卫星的研究处于起步阶段,重力卫星星间高精度测距技术也在重点攻关之中。为此,文章主要介绍双频GPS接收机在重力卫星星问高精度测距中不可或缺的作用,并提出一种利用双频GPS观测量进行修正KBR测距的工程化方案,为我国后期的卫星重力探测计划提供工程参考。
1 测量系统组成
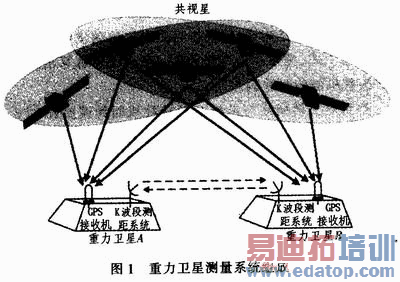
整个重力卫星星座由两颗相距200 km,轨道高度500 km的卫星组成,每颗卫星都搭载了高精度双频GPS接收机、K/Ka双波段(24/32 GHz)测距系统和高精度的时钟等(每颗卫星上搭载的GPS接收机和KBR的时间标准采用同一个振荡器)如图l所示。两星间精密测距的基本思路是:首先利用K波段测距系统(KBR)对两星之间的距离进行测量。与此同时,A星和B星利用其各自的可视GPS导航星进行绝对定位与定时,再通过共视GPS导航星进行相对定位与定时,并利用GPS相对定位与定时结果修正KBR测距,使其测距精度达到微米级。
2 GPS定位结果修正KBR测距
2.1 KBR双向测距及时间同步误差
重力卫星A和B间通过KBR系统进行精密双向测距,其测距原理如下。
重力卫星A在理想真实时刻t对重力卫星B载波信号的观测量可以表示为:

式中,trA、trB分别为重力卫星A和B的KBR时标;CA(tr)、CB(tt)分别为重力卫星A和B在信号接收时刻和发射时刻的钟差;dCA(tr)、dCB(tr)分别为重力卫星A和重力卫星B在接收时刻的钟漂。钟漂对KBR相位的影响仅仅发生在信号发射至接收这一时段 (r≈0.7 ms),只要钟漂达到10-10,就可以达到1/1000周的测相精度,因此,影响测相精度的主要误差是时标ttA、trB的同步误差。
2.2 双频GPS观测量修正KBR测距误差
对重力卫星星座而言,为满足几百公里空间分辨率的重力场测定精度,要求两颗卫星之间的测距精度可达到几个微米。卫星的KBR采用32.7/24.5 GHz频率信号(波长约1 cm),为此,测相精度必须达到千分之一周(1/1 024)。经调制后的差频信号分别为502和670 kHz,为保证1O-4周的测相精度,定时精度应达到10-4/670 kHz=150 ps(O.15 ns),这一精度对在轨振荡器而言几乎是不可能的。利用IGS产品,采用精密定轨(POD)技术,可确定KBR测量的绝对时标和卫星的位置,位置精度可达到2~3 cm,测时精度可达到0.1 ns,可满足KBR时标的要求,因此,GPS地面数据处理系统是KBR达到微米级精度的关键技术之一。重力卫星星载GPS接收机承担的主要任务在于:
1)利用GPS确定的载体卫星厘米级精度摄动轨道恢复长波长项的重力场;
2)利用GPS绝对定时结果消除星载振荡器的长期钟漂;
3)利用GPS相对定时结果校准K波段测距的同步误差,精度为0.1 ns(3 cm)。
总体上,相对定位和相对定时采用事后处理方案,以GPS双频载波相位观测值为基本观测量,辅以载波相位平滑伪距,动力学平滑等多种处理手段,获得模糊度固定坐标解。首先对观测数据进行质量检测,修正载波相位可能发生的周跳,剔除具有粗差的观测值。以一天观测弧段为处理单元,前后延伸3 h,即前一天21:00至第二天的3:00,共30 h,以便内插GPS卫星IGS精密星历。
采用载波相位相对定位的关键是正确确定整周模糊度,采用整数解可以提高坐标解的稳定性和精度。但是,为了消除电离层误差,必须采用L3组合,而L3不具备整数解。测相伪距双差观测方程(以距离表示)可以化为:

式中,实质上就是双差宽波模糊度,具有整数特性,如果能够通过其他途径固定,那么在L3中的模糊度未知数只存在L1的双差模糊度,而且应为整数,其系数正好等于窄波的波长(11 cm),这样就将L3转化为具有整数模糊度估计的观测模型。宽波双差模糊度可以由宽波双差和Melbourne-Wubbena组合联合求解。
由于载波相位测量的精度远高于伪距测量精度,因而高精度时间同步可以通过载波相位测量来实现。相对定时则采用单差模式,由于接收机钟差的存在,很难获得单差模糊度的整数解。为此,首先进行精密相对定位,获得1~2 cm精度的差分定位结果和基线方差。其次将基线结果作为具有先验精度信息的坐标参数代入单差观测方程,从而解算出高精度的相对钟差。
两星载GPS接收机间的载波相位单差观测方程可表示为:
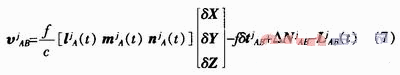
式中,为测量残差,为星载GPS接收机A的位置坐标修正向量,为星载GPS接收机A与星载GPS接收机B间的时钟偏差,为单差模糊度。
由式(7)即可得到两星载GPS接收机间的时钟偏差:
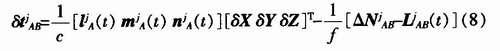
利用双差载波相位进行精密相对定位获得GPS接收机A的位置坐标修正向量,将其作为具有先验精度信息的坐标参数代入上式,搜索出单差模糊度,即可解算出两星载GPS接收机间的时钟偏差。
然而由于模糊度与星载GPS接收机时钟误差及GPS卫星钟差是耦合的,单差方程仅仅消除了GPS卫星钟差的影响,星载GPS接收机起始相位未知的问题仍然存在,因而单差模糊度无法以整周的形式求解。为此,需对单差方程进行重新整合,假设选取第r颗GPS卫星为参考星,以上角标ref表示,则式(8)可以写成:

通过上述重新整合后,式中的变为双差模糊度,满足模糊度整周特性,可以利用整周模糊度搜索方法进行搜索,其中参考星的双差模糊度变为零,其单差模糊度是一个不变的量,可以通过最小二乘估算出来。
在研究精密相对定时时,还需要考虑参考站的绝对钟差对相对定时的影响,因此还可以先考虑求解参考站的绝对钟差。目前JPL利用地面高精度时间参考基准确定的GRACE卫星绝对钟差精度达到O.1 ns,在绝对定时过程中,还要考虑相对论的影响。
通过以上过程便可利用GPS相对定位和定时结果消除星载振荡器的长期钟漂同时校准K波段测距的同步误差,使KBR测距达到微米级。
3 仿真器试验验证
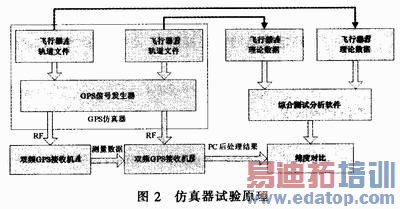
为了验证以上方法的可行性和定位精度,设计了仿真器静态和高动态试验。用双频接收机接收仿真器双频数据,用双频相对定位软件对原始观测数据进行处理并与理论值进行对比,验证精度。试验方法如图2所示。各试验的相对测量结果如表l所示。
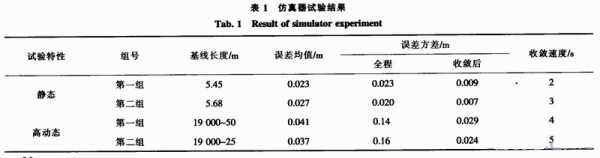
3.1 静态试验
为验证该双频相对测量算法的性能,首先利用静态定基线试验对其验证。试验共两组,仿真器输出静态定基线双频信号,利用双频相对定位软件对原始观测量进行后处理,处理结果与理论数据对比,其结果如图3和图4所示。
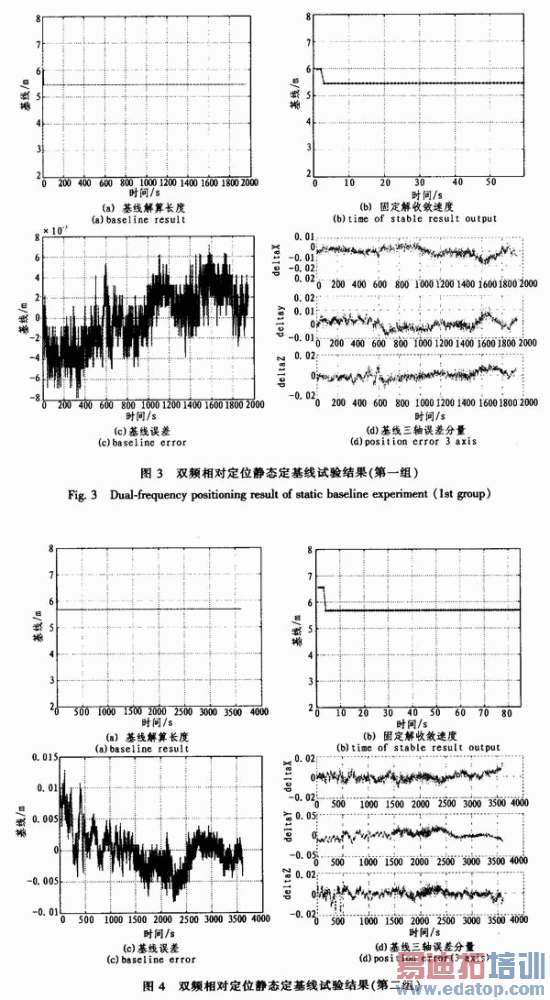
由以上2组试验分析结果可以看出,利用该双频相对定位软件可以稳定地进行基线解算,基线解算结果与理论值一致,固定解收敛后误差可以控制在2 cm以内。从图3(a)、图4(a)可以看出,初始几个历元的基线解算误差较大,这是由于浮点解尚未收敛,且由于静态条件下载波相位双差观测方程法方程病态性,小的测量误差就会带来较大的定位误差。随着观测历元的增加,法方程的病态性得到改善,浮点解逐渐收敛于稳定的实数解。在浮点解收敛、模糊度整数解固定后,便可得到稳定的高精度的解算结果,且精度均小于1 cm。
3.2 高动态试验
为验证该双频相对测量算法在高动态条件下的性能,设计了高动态试验。利用仿真器高动态轨道验证算法在高动态下的性能,和双频相对定位软件对原始观测量进行处理,处理结果与理论数据对比,其结果如图5和图6所示。
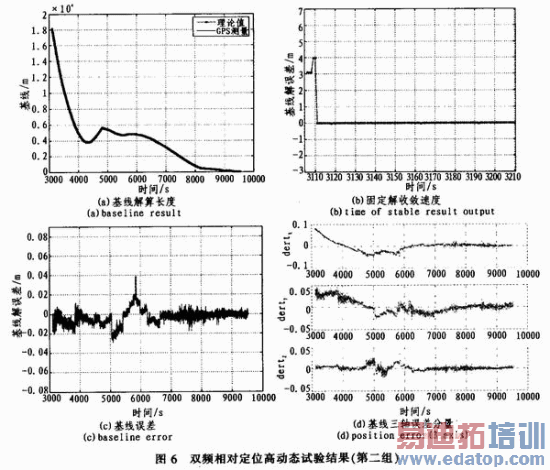
通过高动态试验可以发现利用双频GPS精密相对测量算法可以稳定地进行基线解算,解算结果与理论值一致。在定位收敛后,该算法能稳定地输出高精度的相对定位结果,且误差方差均小于3 cm。
4 结论
地球重力场的精确测量对大地测量、地球物理、地球动力学和海洋学等学科的发展具有极其重要的意义,高精密的GPS相对定位和定时是保证KBR测距精度,进而保证地球重力场测量空间分辨力的基本前提。文章通过分析重力卫星KBR测距任务中星载GPS的作用设计了一种工程化应用的双频组合方法,并给出适用于实际工程的解模糊度方法,通过仿真器试验验证无论在静态还是在高动态条件下该方法解算收敛时间均小于5 s,解算稳定后定位精度均小于3 cm,从而可以满足利用GPS结果修正KBR测距的要求。
上一篇:DPO抓住DSO抓不住的波形瞬间
下一篇:嵌入式环境下串行帧通信的设计


