基于ANFIS的温湿度控制

温湿度控制现如今已经广泛应用于人们的生产和生活中，如何能够准确的控制这两个变量一直是人们研究的问题。传统的方法是通过温度计、湿度计测量数据然后人为操作仪器升温、加湿、通风、降温和除湿，这种方法不仅精确度低、实时性效果差，而且对于操纵人员的要求高、劳动强度大，并且浪费时间和人力。现在采用的是智能化的检测与控制，不但精度和实时性有所提高，而且操作简便。如何能够准确实时的将系统控制在理想的范围是人们一直研究的问题和努力的目标。

如今照明行业的LED灯越来越多，高品质的灯需要经过严格的实验测试才能达到5万小时以上的照明时间，其中就包括在温湿度环境的烧机实验。本文主要介绍ANFIS，然后将该系统应用到LED温湿度环境的测试控制中。

1 ANFIS的结构

Takagi和Sugeno在1985年提出了一种新的模糊推理模型，称为Takagi—Sugeno(T—S)模型。该系统模型可使用极少数的模糊规则生成较繁杂庞大的非线性函数，具有计算效率高、输出连续性、不但能够将线性系统理论知识很好的结合而且非常适合数学分析的特点。自适应神经网络模糊推理系统由T—S型模糊推理系统与人工神经网络相结合，该系统具有模糊推理系统和人工神经网络各自的优点，其最大的特点是根据已知数据就可以对控制系统进行建模，因此可以不需要事先知道被控系统的系统特性，或者对于系统特性比较复杂以及系统特性不明显的控制系统，选用ANFIS往往能够得到比传统的控制方法更好的结果。

根据以上分析，论文采用基于T—S型模糊推理系统。该系统具有强大的自学习能力和非线性外推特性，其本质是通过学习训练数据来实现输入变量到输出变量的线性或非线性映射，并在得出该映射关系后给出输出变量的估计值。

图1是一个典型的基于T—S型模糊神经推理系统的两个输入和一个输出的ANFIS的结构图。一共分为5层。

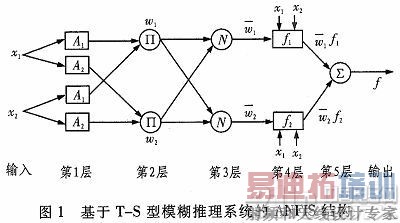
第1层：本层为条件参数。该层的每一个节点都是一个有节点函数的自适应节点，该层的节点函数是模糊集合的隶属度函数，由它确定输入x1(或x2)满足论域A的程度。

Oij=μAji(xj)，i=1，2;j=1，2

论域A的隶属度函数包括高斯函数、三角函数和钟型函数等，可以是任意一种合适的参数化的隶属度函数。下式给出的是gauss隶属度函数的表达式：

2 自适应模糊神经网络的控制算法

减法聚类是一种密度聚类的算法。它是估计一组数据中聚类中心位置和聚类个数的快速的单次算法。减法聚类中每一个数据点都视为潜在的聚类中心，然后依据每个数据点周围数据的密集程度来计算该点被当做聚类中心的可能性。其实现过程如下。

1)计算各个数据点的密度情况。对于m维空间的n个数据点(x1，x2，…，xn)，我们认为每一个数据点都可能是聚类中心的候选者，于是各个数据点xi处的密度目标定义为：

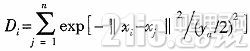
其中，ya是一个正数并且定义了一个邻域数据点。

2)第1个聚类中心是选取具备最高密度目标的数据点，并且依此修正每一个需要作为聚类中心数据点的密度目标。令Dc为其密度目标，xc为选中的点，则每个数据点xi的密度目标可以通过下式修正，即

其中，yb是一个正数。由上所述靠近第1个聚类中心xc1的数据点密度目标会不断减少，因此作为下一个聚类中心这些点是不可能的。

3)选定下一个聚类中心xc2一再次修正数据点的所有密度目标。

重复上述过程，如果上式达到最小值，则聚类结束。

减法聚类是以密度为聚类的算法，它应用于一个输入、输出数据集，依据数据集的聚类集个数和聚类中心的位置，能够实现将输入空间得到最优的划分，并且确定输入以及输出语言变量的隶属度函数的个数和模糊规则数。本文首先通过减法聚类得到最初始的模糊推理系统，再通过输入输出数据对系统进行进一步的优化，最终得到一个很合理的模糊推理系统。

3 ANFIS的参数学习方法

由自适应神经模糊推理系统中所涉及的参数一般都比较多，故对于ANFIS的条件参数和结论参数的训练和确定，必须采用一种高效的参数学习方法。本文选用一种“混合算法”，该方法由Jang最早提出的，条件参数的修正使用反向传播，结论参数修正选用线性最小二乘估计算法。其目的是为了提高ANFIS训练数据学习的速度，尽可能快地确定最优的系统参数值，最终使得系统输出结果的误差平方和最小。

混合学习算法的整个学习过程如表1所示。

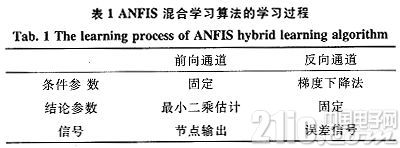
模糊神经网络的学习算法是通过2步组成：首先将条件参数固定，输入信号沿着网络正向传送至第4层，选用最小二乘法算法预估后件参数，信号继续正向传送至第5层输出层;然后将得到的误差信号沿着通道反向传播，使用BP算法调整条件参数。这样通过梯度下降法不但可以降低搜索空间的维数，还可以很好的提升参数的收敛速度。

本网络系统中需要考虑的学习参数主要是条件参数{mji，σji}和结论参数{aji，j==0，1，2;i=1，2}。

定义目标函数为

式中：d为系统期望输出或者教师信号。

误差信号由第5层依次反向传递至第1层，具体算法：

4 自适应模糊神经控制器设计

图2为根据自适应模糊神经网络控制的控制器，此控制器不但保持了常规串级控制，而且采用主、副控制器。主控制器使用一个模糊神经控制器和一个智能PI控制器来控制系统，副控制器仍然采用P控制器。

输入变量的线性组合为自适应模糊神经系统的模糊规则，即：

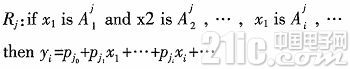
式中：i=1，2，…，n;j=1，2，…，m;Rj为第j条模糊规则所表示的模糊蕴含关系;为xj的第j个语言变量值，pj的后件网络的连接权值。如果输入量使用单个模糊化的方法，则对于系统给定的输入x，可以求得关于每条规则的适应度为

式中：

是第i个输入分量隶属于第j个语言变量模糊集合A的隶属度函数。

模糊系统的输出量为每条规则的输出量的加权平均，即

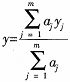
aj为对于给定的输入x所求得的对于每条规则的适应度。

智能比例积分(PI)控制器是具有PI环节和使能端的逻辑判断子系统的2个模块组成。系统所处的状态通过逻辑判断子系统和的符号来判断，从而控制P1环节是否有效。定义误差e=r-y，误差变化率ec，当e·ec>0或e=0、ec≠0时，PI控制器功能有效，主控制器由模糊神经网络控制器和PI控制器共同作用控制实现，而当e·ec<0或ec=0时，PI控制器功能失效，主控制器模块由模糊神经网络控制器单独来控制。结合经验知识，在仿真过程中通过对系统调试，最后确定的参数kp=1.2，ki=100。

5 ANFIS的仿真结果

温度的偏差e和偏差变化率ec(湿度的偏差e和偏差变化率ec)为控制器的两个输入变量，E、EC为其对应的模糊化变量，[-6，+6]为E和EC的基本论域。通过查询常规温度模糊控制系统的训练样本表格和数据，神经模糊推理编辑器将训练所得到的样本数据载入训练数据集，7定义为输入变量的隶属度函数的数目，类型为高斯型，输出变量的隶属度函数

类型为常数型.假设训练的最初步长为0.01，目的误差为0，最后模糊推理系统经过400步训练后生成。为了形成对比本文对常规PID控制器和本文所研究的自适应模糊神经网络控制器，在无外界扰动和有外界扰动的两种情况下，进行了仿真，仿真结果见图3和图4。

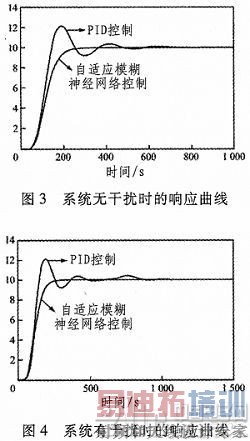
从图片的结果可以看出，自适应模糊神经网络控制器拥有良好的动、静态特性和抗干扰能力，同时该控制器性能明显比常规PID控制器要好，实现起来比传统的PID控制简单且基本没有超调。

6 实际应用

本文采用Sensirion公司的SHT75温湿度传感器，该产品是该公司推出的一种插针式同时具有高精度版本的温湿度传感器。SHT75经过完全标定，传感器具有高质量以及能够提供高精度数字输出。同时该产品是80uW的低能耗，相对温度工作范围：-40～+125℃，具有±0.3℃的精度。湿度工作范围：0～100%，具有±1.8%RH的精度。

该控制器在现场使用时，根据SHT75测量的温度值，反馈到系统显示界面，根据反馈的数值决定设备是工作还是不工作。最终了解到随着时间的不断延长，自适应模糊神经网络控制能够将该系统的温度维持在一个比较理想的范围内。

7 结论

针对温湿度控制系统存在的延时时间长、惯性强等特点，本文所研究的自适应模糊神经网络的控制方法不仅克服了常规PID控制具有的自适应能力差的缺点，而且本文采用的模糊控制器解决了常规的模糊控制器存在的稳态精确度低和模糊系统规则难以把握等缺点。该控制方法不仅仅对于本文提出的温湿度控制系统有效，同时对于复杂的被控对象也能取得比较好的控制效果，能够展现出比较好的系统稳定性、抗外界干扰性和系统动态特性等优点，具有较高的工程应用价值。