基于DSP的ILS机载接收机基带信号处理

1 引 言

着陆是飞机航行过程中最为重要的一个阶段，据统计，超过60％的飞行事故发生在飞机的着陆阶段。这是因为在着陆过程中，要求飞行员必须在比较短的时间内完成很多标准化的操作。而依靠目视着陆，对气象条件要求较高，一般要求飞行高度300 m时，水平能见度大于4.8 km，否则难以保障安全着陆。因此为了保证飞机能在恶劣气象条件下能够安全着陆，必须使用无线电导航系统为飞机提供高精度的定位引导信息，实时给出飞机与给定下滑航道的偏差程度。而仪表着陆系统(Instrument Landing System，ILS)是当今世界上应用最为广泛的无线电着陆引导设备之一。

常规的ILS系统机载导航接收机基带处理部分是采用模拟电路实现的，电路复杂；设备体积大，功耗高，且精度不高。本文采用DSP器件为基带信号处理核心部件，将基带信号全部在数字域中进行处理，采用数值滤波和多速率处理算法，简化了电路设计，降低了设备功耗的体积。本文给出的算法在以一片TMS320C2812F芯片为处理核心，无外扩存储器的信号处理板上进行了半实物仿真，仿真结果验证了算法的有效性和可靠性。

2 ILS基带信号数学模型

ILS系统地面设备包括航向台、下滑台和信标台三个部分。航向台和下滑台都是利用空间相交的双针状天线方向图，以等信号区的形式分别提供与水平面成一定角度的下滑面引导，与水平垂直的航向引导。因此航向台和下滑台的接收机基带处理部分是一样的。ILS的基本原理及其信号处理方法参见文献[1，2]。

ILS基带信号是一种DSB信号，导航信息由信号各个频率上的幅度表示。基带信号可以简单表示为：

在ILS系统中，规定频率f1=90 Hz，f2=150 Hz，f3=1 020 Hz，并规定基带信号的采样率为fs=12 583 Hz。因此基带信号处理的核心就是如何准确计算式(1)中各个频点上的幅度大小。

最简单的方法就是采用DFT进行计算，然而这种方法在实际过程中性能并不令人满意。首先要利用DFT算法，就必须考虑信号的采样率和信号的时间长度，显然信号的时间长度越长，频率分辨率越高，而同时信号的采样率越高，频率的估计精度就越高，而这些条件与算法所需的存储空间存在矛盾。其次因为ILS的各个信号频率允许存在一定频率漂移，其中频率f3容许的漂移达到±50 Hz，而其他的频率也存在几个Hz的漂移，若要利用DFT算法，就必须准确估计当前信号的各个频点的大小。估计频率的准确值方法很多，但要求在DSP上实现，就必须考虑DSP的运算速度和存储空间的限制。文献[2]给出了在TMS320VC5402上实现的基于频域的实现方法，显然处理更加复杂，运算量大且软件占用存储空间大。

因此本文采用滤波器进行滤波的方法，将各个频点的信号进行滤波，得到单频信号，再从时域上计算信号的幅度。直接将各个频率分量进行滤波也是不可行的，这是因为频率f1和f2比较低，如果要设计一种滤波器能够仅将频率f1滤出，而要求对频率f2有较大的抑制程度，则该滤波器的长度会非常长，甚至大于200阶，这不仅增加了算法对存储空间的需求，还增大算法的处理时间。因此本文采用针对不同的信号频率，采用不同的采样率，从而保证各滤波器长度较短，且处理时间较快。

3 ILS基带信号处理的DSP实现

本文采用TMS320F2812 DSP为处理核心的信号处理板实现，为了提高处理速度，降低对存储空间的要求，本文中所有的数字滤波器长度均为33。由于信号的采样率较高，因此首先进行3倍的降采样，为了防止带外混叠，在降采样之前还增加了抗混叠滤波器H1。将信号记录1 000个点作为信号处理用，进行存储，存储格式为双字节数据。算法首先将该数据进行均值计算，得到参数A0，并从信号中减去该直流分量。

信号的预处理如图1所示，得到的数据是4 B的浮点数，数据长度为1 000。对该数据的处理如图2所示。

对于频率f3=1 020 Hz信号分量，由于其频率较高，无需1 000个数据全部参加运算，因此首先通过一个数据选通步骤，只选取其中的125个点送入高通滤波器H2，可以得到纯的单频f3信号。而对于频率f1=90 Hz，f2=150 Hz两个信号分量，其频率较低，必须首先经过8倍抽取，降低采样率，才能减轻对后续滤波器设计的要求。因此8倍抽取后，数据的长度为125点，再分别经过低通H5和高通H4得到对应的频率f1=90 Hz，f2=150 Hz两个分量信号。

这里有几个问题需要说明。由于是对正弦信号进行采样，从时域进行幅度估计，首先要解决的是幅度估计精度的问题。因为采样周期与信号周期不一定满足整数倍关系，也就是说正弦信号采样后的各周期的最大值点不一定对应的就是正弦信号的最大值点，假定采样信号的最大值点与实际信号最大值之差在△d以内，则采样率最小值由下式决定：

从式(2)可以看出：△d一定时，信号的频率f0与采样率最小值成正比关系，或者说，提高信号的采样率，可以降低信号幅度估计精度。因此本文中将所有信号进行了2倍插值。

从图2还可以看出：

(1)信号经过滤波后再进行8倍抽取，这种算法意味着数据1 000个点全部参加滤波运算，然而其中输出值只利用了其中1／8。显然这种方式是浪费了运算时间，因此本文采用多相结构，提高运算速度。而图1中的三倍抽取也可以用多相结构实现。

(2)进行处理的数据均为125点，输出数据均为250点，因此这些数据可以公用存储空间，滤波器H6，H7和H8结构是一样的，因此可以用一个存储空间存储滤波器系数。

(3)信号是经过若干个滤波器进行分别处理的，因此信号的幅度还受到滤波器的影响。在实际工作之前，还需要进行定标处理。定标方法是通过给定信号源，分别测定每路信号的衰减程度。

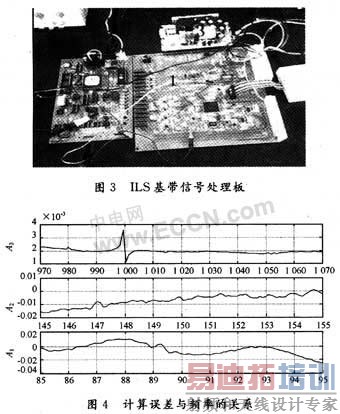
ILS基带信号处理板如图3所示，其中标注1的是信号处理板，标注2的是信号源模块，标注3的是电源模块。每批次数据的运算速度为528 ms，基本满足实际需要。

图4给出了各频点上幅度估计误差与频率的关系。导致误差随频率变化的原因主要由滤波器的特性，以及采样率与信号频率之间的比值关系决定。其中滤波器特性的影响主要是影响误差随频率的慢变成分，而信号频率与采样率关系的变化则会导致误差随频率的快变。从图4可以看出，对于低频分量，估计误差可以控制在2％以内，而高频分量的估计误差则更小。

4 结语

仪表着陆系统是国际目前通用的飞机着陆设备。常规的ILS机载接收机基带信号处理部分采用模拟电路实现，测量精度低，电路实现复杂。本文基于DSP器件，基带信号处理部分全部在数字域进行，采用了定长的FIR滤波器和多速率信号处理算法，并针对硬件条件，对软件的处理速度和存储空间进行了优化。将该软件在DSP TMS320F2812系列开发板上进行了仿真，计算结果稳定、精确，总体性能优于常规ILS机载接收机基带信号处理模块。