- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
齿顶圆与齿根圆直径的测量及其量具
录入:edatop.com 点击:
在进行齿轮测绘时,通常是测量齿顶圆直径、齿根圆直径,以此确定齿轮各主要参数。但在测量时,有时难以实现,如在测量奇数齿轴齿轮时,必须先测一些有关的量,再进行间接换算才行。由于间接测量,其误差大、精度低,如采用光电仪器测量,成本又较高,一些工厂难以实现。本量具不但解决了有轴孔的奇数齿轮齿顶圆和齿根圆直径的测定,也解决了奇数齿轴齿轮的测定,对偶数齿齿轮及大轴径均可测量。
1三点定圆原理
OO′sinβ=OA (1)
OA=OB=OC=d/2 (2)
O′C=OO′-OC (3)
将式(1)、式(2)代入式(3),则
O′C=d/2sinβ-d/2
=(1-sinβ)d/2sinβ (4)
d=2sinβO′C/(1-sinβ) (5)
式中β和O′C可测出,所以d值可求。
2量具结构
利用上述关系式,设计了专用量具,固定角β后测得O′C值,代入式(5)计算即可。
量具结构如图2,主要由测量爪1、角度盘3、读数头4组成。
测量时采用面接触,测量爪1的工作面通过自己的回转中心并延伸到另一侧,以便确定β角。测量爪用螺栓固定在回转中心上,为保证其稳定性和准确性,调整β角后,再用螺栓3将测量爪固定在角度盘上(两侧测量爪对中线夹角β相等)。
2.2读数头
读数头4选用千分尺结构,为实现标准化,可采用标准深度千分尺读数 ,用以测量O′C值。
2.3角度盘
角度盘2为量具主体,上面刻有供测量爪调整角度的刻度和装配测量爪用的中心(即测量爪回转中心)孔,同时在角度盘对称线上加工出装配读数头用的配合孔,装配时采用过盈配合。
2.4量具的调零
将量具在一个标准环上通过标准读数头的微调零装置调零(即测量爪中心)。
3齿轮测量
3.1测量齿顶圆直径da
无论奇数齿或偶数齿齿轮,测量时调整β角(图3),确保两测量爪(图中AO′、BO′)工作面与轮齿中线附近(OA、OB)的齿顶圆相切,转动读数头旋钮,使伸入端O′C顶到中间轮齿的齿顶C点上(跨齿数为奇数),读出O′C值,并将O′C和β值代入式(5),即可计算齿顶圆直径
da=2sinβO′C/(1-sinβ) (6)
如图4,O′A、O′B为两测量爪,调整β角,使测量爪工作面与齿轮轮齿中线附近齿顶相切,转动读数头旋钮,使伸入端OE顶到齿根圆E点上(跨齿数为偶数),读出OE值,由于
OO′=AO/sinβ=da/2sinβ (7)
OE=df/2=da/2sinβ-O′E
df=da/sinβ-2O′E (9)
3.3齿轮参数的确定
完成da、df的测量,即可按通常方法计算齿轮的各参数。
4注意事项
调整β角时,应使两测量爪与角度盘对称线的夹角β相等;测量时尽量调整到使测量爪与轮齿中线附近的齿顶圆相切;测量齿顶圆时,跨齿数为奇数;测量齿根圆时,跨齿数为偶数;测量时,使测量爪所在平面与被测齿轮轴线垂直。
5量具的误差分析
作为量具,首先必须要满足精度要求。
5.1量具的系统误差
由式(5)可知,夹角误差和读数头误差直接影响系统误差。
由于误差比较小,对式(5)全微分,得
Δd=2sinβΔΟ′C/(1-sinβ)
+2O′CcosβΔβ/(1-sinβ)2 (10)
由此可见,2sinβ/(1-sinβ)为常数,这说明ΔOC对Δd的影响为固定线性关系;而O′Ccosβ/(1-sinβ)2与O′C的值成比例关系,说明Δβ对Δd的影响关系与被测直径成比例关系。以上说明系统误差是有规律的,设计制造时尽量减小那些对直径误差影响较大的参数误差。设计制造后,可通过修正系数消除系统误差。
5.2随机误差
测量过程中,测量力的大小、量具的变形、测量时的温度、夹持位置的不同及读数误差等,都会产生一些不确定的误差,这些误差,可通过控制测量环境和反复多次测量等手段将其降到最小程度,使之满足测量要求。
6结论
对实际齿轮进行测量,结果表明原理正确、结论可靠;量具结构简单,便于制造,易推广,且可用于大轴径和圆弧面曲率半径的测量,误差适中,体积、重量适当,便于测量。(end)
1三点定圆原理
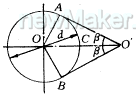
图1
OO′sinβ=OA (1)
OA=OB=OC=d/2 (2)
O′C=OO′-OC (3)
将式(1)、式(2)代入式(3),则
O′C=d/2sinβ-d/2
=(1-sinβ)d/2sinβ (4)
d=2sinβO′C/(1-sinβ) (5)
式中β和O′C可测出,所以d值可求。
2量具结构
利用上述关系式,设计了专用量具,固定角β后测得O′C值,代入式(5)计算即可。
量具结构如图2,主要由测量爪1、角度盘3、读数头4组成。
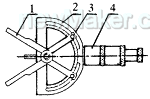
图2
测量时采用面接触,测量爪1的工作面通过自己的回转中心并延伸到另一侧,以便确定β角。测量爪用螺栓固定在回转中心上,为保证其稳定性和准确性,调整β角后,再用螺栓3将测量爪固定在角度盘上(两侧测量爪对中线夹角β相等)。
2.2读数头
读数头4选用千分尺结构,为实现标准化,可采用标准深度千分尺读数 ,用以测量O′C值。
2.3角度盘
角度盘2为量具主体,上面刻有供测量爪调整角度的刻度和装配测量爪用的中心(即测量爪回转中心)孔,同时在角度盘对称线上加工出装配读数头用的配合孔,装配时采用过盈配合。
2.4量具的调零
将量具在一个标准环上通过标准读数头的微调零装置调零(即测量爪中心)。
3齿轮测量
3.1测量齿顶圆直径da
无论奇数齿或偶数齿齿轮,测量时调整β角(图3),确保两测量爪(图中AO′、BO′)工作面与轮齿中线附近(OA、OB)的齿顶圆相切,转动读数头旋钮,使伸入端O′C顶到中间轮齿的齿顶C点上(跨齿数为奇数),读出O′C值,并将O′C和β值代入式(5),即可计算齿顶圆直径
da=2sinβO′C/(1-sinβ) (6)
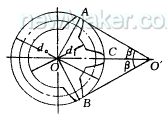
图3
如图4,O′A、O′B为两测量爪,调整β角,使测量爪工作面与齿轮轮齿中线附近齿顶相切,转动读数头旋钮,使伸入端OE顶到齿根圆E点上(跨齿数为偶数),读出OE值,由于
OO′=AO/sinβ=da/2sinβ (7)
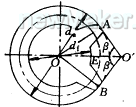
图4
OE=df/2=da/2sinβ-O′E
df=da/sinβ-2O′E (9)
3.3齿轮参数的确定
完成da、df的测量,即可按通常方法计算齿轮的各参数。
4注意事项
调整β角时,应使两测量爪与角度盘对称线的夹角β相等;测量时尽量调整到使测量爪与轮齿中线附近的齿顶圆相切;测量齿顶圆时,跨齿数为奇数;测量齿根圆时,跨齿数为偶数;测量时,使测量爪所在平面与被测齿轮轴线垂直。
5量具的误差分析
作为量具,首先必须要满足精度要求。
5.1量具的系统误差
由式(5)可知,夹角误差和读数头误差直接影响系统误差。
由于误差比较小,对式(5)全微分,得
Δd=2sinβΔΟ′C/(1-sinβ)
+2O′CcosβΔβ/(1-sinβ)2 (10)
由此可见,2sinβ/(1-sinβ)为常数,这说明ΔOC对Δd的影响为固定线性关系;而O′Ccosβ/(1-sinβ)2与O′C的值成比例关系,说明Δβ对Δd的影响关系与被测直径成比例关系。以上说明系统误差是有规律的,设计制造时尽量减小那些对直径误差影响较大的参数误差。设计制造后,可通过修正系数消除系统误差。
5.2随机误差
测量过程中,测量力的大小、量具的变形、测量时的温度、夹持位置的不同及读数误差等,都会产生一些不确定的误差,这些误差,可通过控制测量环境和反复多次测量等手段将其降到最小程度,使之满足测量要求。
6结论
对实际齿轮进行测量,结果表明原理正确、结论可靠;量具结构简单,便于制造,易推广,且可用于大轴径和圆弧面曲率半径的测量,误差适中,体积、重量适当,便于测量。(end)


