基于MSP430与FPGA的多功能数字频率仪设计*

作者/ 任欢 颜逾越 厦门大学嘉庚学院 信息科学与技术学院(福建 漳州 363105)

摘要：本文采用以FPGA为主，MSP430为辅的框架系统处理方式设计了多功能数字频率仪。该装置采用低频直接测周期，高频等精度多周期同步测量的方法，通过进一步优化标准时钟频率的设置，克服了传统测频方法在高精度要求方面的缺陷。将MSP430作为控制处理核心、FPGA作为信号处理单元，将高效控制与快速运算能力相结合，实现正弦波频率、两路方波信号时间间隔以及矩形脉冲占空比的测量。测试表明，该装置具有高精度、高稳定性、装配简易和操作便利的特点。

引言

　　随着电子产业的蓬勃发展，新兴产业对频率等参量测量结果的快速性、稳定性、精确性等性能指标提出了更高的要求^[1]。目前，信号频率的测量已有多种测量方案，如过零检测法^[2]、离散傅里叶变换^[3]、离散卡尔曼滤波^[4-5]等。其中存在对高频信号的快速测量的局限性、频谱泄漏^[6]以及准确性有待提高^[7]等问题。本文采用高速现场可编程逻辑阵列(FPGA)及超低功耗单片机(MCU)，结合多周期测量原理，通过进一步优化标准时钟信号频率的设置，使用低频时钟计数法直接测周期，高频等精度多周期同步测量法测频率的方法，实现对待测信号频率、占空比、两路信号时间间隔等参量的高精度测量。

1 系统设计思路

　　1.1 系统总体结构

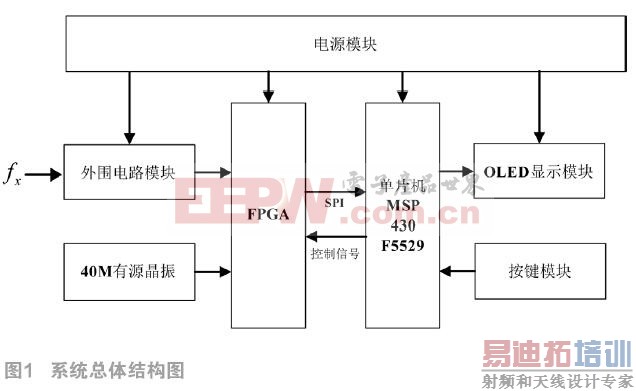
　　系统由Altera公司CycloneII EP2C8Q208C8型号FPGA、TI公司MSP430F5529型号MCU、外围电路模块、显示模块、按键模块和电源模块构成，系统的总体结构如图1所示。其中，MCU是本系统的控制中心，主要负责数据接收、逻辑处理和命令传达;FPGA是本系统的核心测量模块，主要负责利用由其内含的计数模块而构成的等精度频率测量模块、高电平时间计数模块、低电平时间计数模块、时间间隔测量模块进行高频信号的频率、低频信号的周期、单路方波信号的占空比和两路方波信号时间间隔的测量，并根据MCU给定的控制信号，通过SPI协议发送相应的测量数据至MCU中;外围电路模块是本系统的输入信号调理模块，主要负责将待测信号f(x)通过一系列的放大、整形等处理输出为FPGA可直接判别并计数的方波信号;显示模块主要用于已测得信号的频率、占空比、时间间隔等参量的显示，并由按键模块进行数据刷新。

　　1.2 时间及频率测频原理

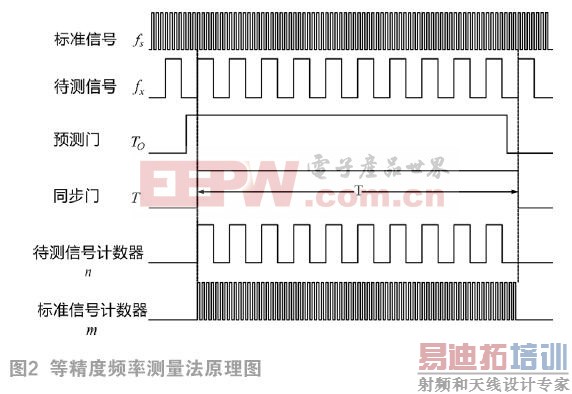
　　等精度频率测量法是指在给定一种标准时钟信号的情况下，通过对待测信号的上升沿进行多次识别及计数，从而得到待测信号频率的方法。等精度频率测量法的原理图如图2所示，若待测信号在标准时钟信号上升沿个数为m的T秒时间内，上升沿个数为n个[8]，则待测信号频率为：

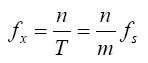(1)

　　其中，f_x为待测信号频率，f_s为标准时钟信号频率。

　　将式(1)进行微分及相应变换可得：

　　其中，d_fs/f_s为标准信号误差，即晶振误差，由于晶振稳定性高，这一部分误差可忽略不计。

　　则频率测量误差为：

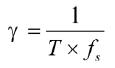(4)

　　由此可见，理论中测量误差与待测信号频率参数无关[9-10]，增长标准时钟信号的同步时间T或增大时钟信号的频率皆可进一步提高测量精度，且等精度测频法无法对频率低于1/T低频信号进行测量。另一方面，在实际测试中，FPGA计数结果可能因硬件延迟存在着两个计数值的固定误差，则有实际误差为：

(5)

　　若要求测量误差小于η时，则符合精度的待测频率f_x的最小值为：

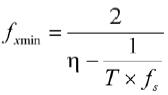(6)

　　直接测周法是一种对待测信号一个周期内标准时钟信号进行计数，从而测量待测信号频率的方法，其测量原理图如图3所示。若标准时钟信号在待测信号一个周期内上升沿个数为m个[11]，则待测信号频率为：

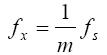(7)

　　同理可得：

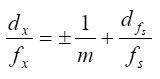(8)

　　同理，省略掉晶振误差，且考虑FPGA硬件延迟后，可得直接测周法的测量误差为：

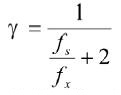(9)

　　由此可见，理论中测量误差与待测信号频率参数有关，若要求测量误差小于时，则符合精度的待测频率fx最大值为：

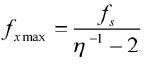(10)

　　若要对低频段采用直接测周法，高频段采用等精度测频法实现对整个通带的信号频率测量，则必须有，即必须将标准时钟信号频率设置为：

本文来源于中国科技核心期刊《电子产品世界》2016年第9期第65页，欢迎您写论文时引用，并注明出处。

　　1.3 外围电路设计

　　外围电路模块的主要作用是通过一系列的放大、整形等处理实现对输入信号的调理，使输出为FPGA可直接判别并计数的TTL信号。首先，FPGA作为一种现场可编程门阵列，只能对数字信号进行操作，因此，调理电路的输出信号幅度不得低于2.4V;其次，由于FPGA为本系统的信号测量单元，且通过捕捉待测信号上升沿来实现对待测信号频率的测量，因此，调理电路输出信号的上升沿必须保证在单个时钟脉冲之内，即要求输出信号的上升时间较短。

　　本系统的外围电路包括高频处理、中频处理和低频处理三个部分。对于高频处理部分，待测信号的频率较高，正弦波无需整形为方波也可视为上升沿，只需进行高增益的放大;低频处理部分先经过放大电路，再经过史密斯触发器整形为方波;中频处理部分先经过放大电路，再经10分频电路后送入低频处理部分的整形电路，从而输出方波。本系统采用TI公司宽带超低噪声电压反馈运算放大器OPA847搭建前级信号放大电路，该芯片带宽增益积可达3.9GHz，电压输入噪声低至，压摆率高达950V/μs。

2 系统实现

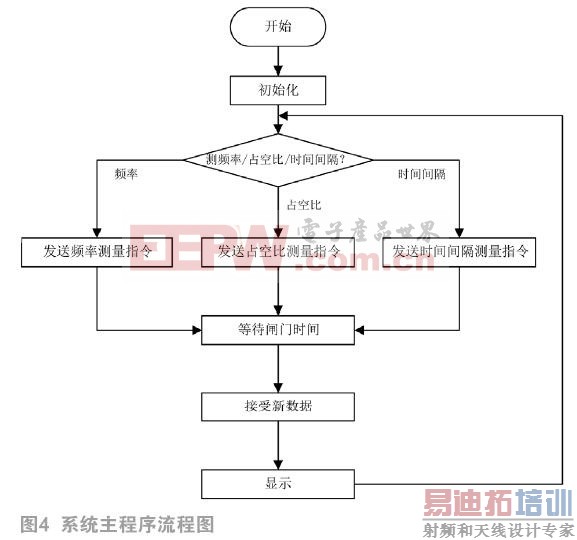
　　MSP430主程序流程图如图4所示，主要包含正弦波频率、两路方波间隔时间和矩形脉冲占空比的测量功能。当按下相应按键时，MCU将向FPGA发送控制信息，使其开始相应参量的测量。当测量结束时，FPGA将测量值通过SPI通信方式传输至MCU中，MCU进行最终计算并显示在OLED12864上。由于FPGA的系统时钟较快，MCU的系统时钟相对较慢，因此，设置MCU为SPI通信的主设备，FPGA为从设备。MCU采用I/O口模拟SPI的模式，由I/O口产生时钟信号SCLK，从而实现FPGA与MCU的数据互传。

　　FPGA模块主要包含顶层文件、测频模块、高电平时间测量模块、低电平时间测量模块、SPI通信模块和时间间隔测量模块等。其中，FPGA晶振产生初始系统时钟，经锁相环按一定系数倍频后为各模块提供时钟信号。MCU通过两根控制线对频率、占空比、时间间隔三种功能进行选择。待测频率的正弦波信号或待测占空比的方波信号经过输入调理电路后都将调理为性能良好的方波信号，该路信号直接与FPGA的测频模块、高电平时间测量模块、低电平时间测量模块相连，从而得到该路信号的频率和占空比。测量两路方波信号时间间隔时，两路输入信号通过输入调理电路的两级放大后，任一路经过1.5倍分频后与第二路信号一同接入时间间隔测量模块，实现对两路等频率、等占空比方波信号超前或滞后情况下时间间隔的测量。

3 测试结果与分析

　　数字频率仪的性能主要取决于测量的精确度、高精度的频率范围、输入电压的幅度值等。频率范围越大，输入电压幅度越低，实现高精度测量越困难。本系统设置FPGA的同步时间为1s，目标频率测量精度高于0.01%，则有：

(12)

　　因此，设置FPGA锁相环倍频系数为5，将40MHz的初始时钟脉冲倍频至200MHz，以满足系统测频精度需求。为了验证本测量系统的稳定性及测量结果准确性，进行了七组试验。

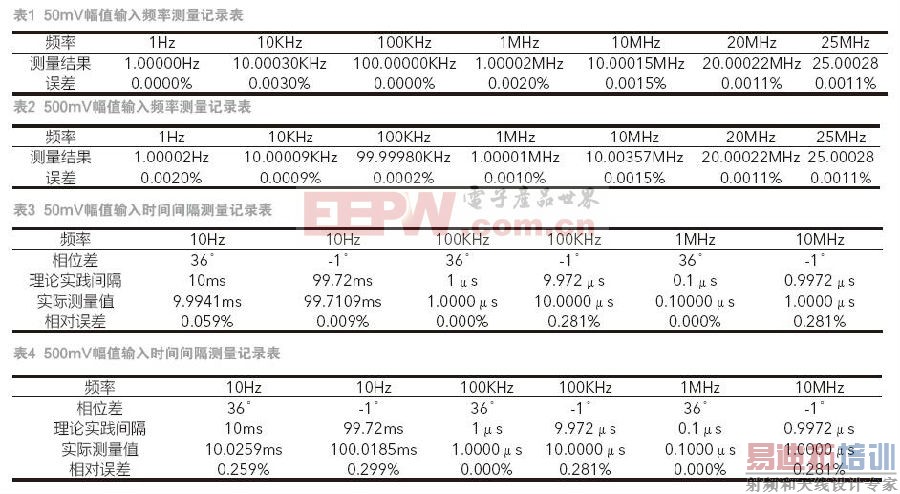
　　首先，在50mV及500mV下，1Hz～25MHz频段范围内，对不同频率值的正弦波进行频率测试，测试目的是验证本系统正弦波频率测量功能的准确性，测试结果如表1及表2所示。从测试结果可知，在1Hz～25MHz频段内，本系统测量结果的相对误差最大值为0.0020%。

　　在50mV及500mV下，10Hz～10MHz频段范围内，对时间间隔为0.1μs～99.72ms的两路方波信号进行时间间隔测试，测试目的是验证本系统时间间隔测量功能的准确性，测试结果如表3及表4所示。从测试结果可知，时间间隔测量结果的相对误差最大值为0.299%。

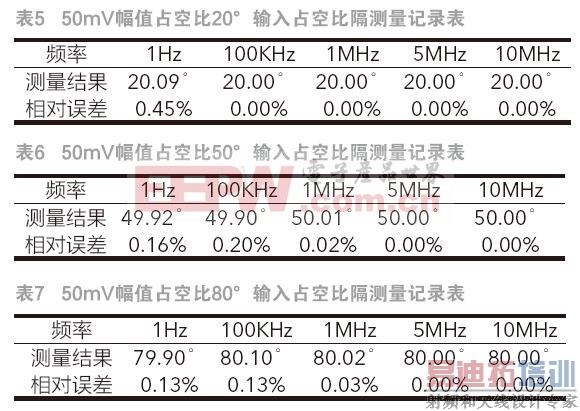
　　在50mV下，对1Hz～10MHz频段范围内的矩形脉冲信号进行占空比测试，测试目的是验证本系统矩形脉冲占空比测量功能的准确性，测试结果如表5、表6及表7所示。从测试结果可知，本系统在该情况下测量结果的相对误差最大值为0.45%。

　　通过以上7 组试验充分检验了系统正弦波频率测量、两路方波信号时间间隔测量、矩形脉冲占空比测量功能的准确性及稳定性，正弦波频率测量相对误差不超过0.0020%，两路方波信号时间间隔相对误差不超过0.299%，矩形波占空比相对误差不超过0.45%，操作过程极为方便，能实现量程的自动切换，具有高精度、高稳定性的特点。

4 结论

　　针对高精度多功能测频的需求，本文提出了基于MSP430与FPGA的多功能数字频率仪，并实现进一步优化标准时钟信号频率的设置。该系统可以实现正弦波频率测量、矩形波占空比测定、两路方波信号时间间隔检测等功能。测试结果表明，该系统完全达到了预定的设计功能，并具有高精度、高稳定性的特点。本设计部分功能仍有待进一步提高与完善，理论上，本测频方法可实现0Hz~200MHz的精准测频。本文尚未对25MHz以上高频输入调理电路的有效放大及1Hz以下低频整形电路的高速整形提出解决方案，尚具有进行功能性完善的空间，届时将具有更好的实际应用价值。

参考文献：

　　[1]张天恒,叶伟,王阳阳,等. 基于SOPC的便携式高精度频率仪设计[J].仪表技术与传感器,2015,05:34-37.

　　[2]易龙强. 基于一元线性回归理论的数字正弦信号频率测量算法[J].电测与仪表,2011,03:20-24.

　　[3]许珉,刘晓辉,王玺,等. 基于加四项Nuttall窗递推DFT插值算法的高精度测频方法研究[J].郑州大学学报(工学版),2013,01:66-69.

　　[4]王科,陈丽华,麦瑞坤,等. 基于扩展卡尔曼滤波频率跟踪的DFT同步相量测量算法[J].电网技术,2014,09:2519-2524.

　　[5]ALAM A S.A new fast algorithm to estimate real-time phasors using adaptive signal processing [J].IEEE Transactions on Power Delivery，2013，28(2)：807-815.

　　[6]李军,王越超. 一种基于幅值调制的新型电力系统正弦频率测量方法[J].电工技术学报,2015,07:144-150.

　　[7]孟卓,温和.基于复化梯形的准同步采样频率测量算法[J].中国电机工程学报,2015,10:2445-2453.

　　[8]偶晓娟,周渭,易韦韦,等. 精密频率测量边沿效应的特性分析[J].西安电子科技大学学报,2016,03:157-162.

　　[9] 陈发喜. 高分辨率时频信号处理技术研究[D]. 西安: 西安电子科技大学 2010.

　　[10] HUANG G Z, LI Z Q, YI Y W. Research of Complete Synchronization Frequency Measurement Method Based on Phase Coincidence[J]. Instrument Technology, 2010, (9): 14-15.

　　[11]罗莉琴,万丽,李远哲,等. 基于MC9S12DT128单片机多路频率量测量模块的设计与实现[J].计算机测量与控制,2015,10:3458-3460+3464.

本文来源于中国科技核心期刊《电子产品世界》2016年第10期第65页，欢迎您写论文时引用，并注明出处。