- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
高阶电路动态特性的仿真分析
作者/ 贺为婷 杨建华 西安工业大学 电子信息工程学院(陕西 西安 710032)
摘要:为了准确直观地观测电路的动态变化过程,采用四种方法对一电路实例进行仿真分析:用积分法求解状态方程,用拉普拉斯变换法求解s域的方程组,用数值积分函数求微分方程的数值解,构建微分方程的Simulink模型观测响应曲线。四种方法的仿真结果完全一致且与电路理论相符。实验结果表明,Matlab程序简洁、可读性强且计算结果准确,同时它形象直观,改变参数方便,能够弥补硬件实验的不足。Matlab在电路理论学科研究与工程实践中都具有很好的应用价值。
引言
高阶动态电路的分析通常都归结为高阶微分方程或一阶微分方程组的求解,需要微分方程和矩阵理论的相关知识,掌握起来比较困难。对于复杂的高阶电路,用求解微分方程的方法则更加困难,一是列写微分方程,二是根据变量及变量的各阶导数的初始值确定积分常数。若借助合适的仿真软件,则可以使电路的分析变得方便、准确和直观。电路仿真是电路分析及电路教学的重要手段,它形象直观,改变参数方便,能够弥补硬件实验的不足[1]。
Matlab是目前最为流行的工程软件之一,它具备强大的计算、仿真和绘图功能,能方便地绘制二维、三维图形和相量图。运用该软件,可以方便地研究各类系统问题,包括电路仿真分析。对于动态过程,用图形来显示会更加直观,它可动态地演示复杂电路各参量的变化过程,从而加深对电路的理解和认识。对于动态过程中某时刻的情况可以有一个定量的认识,对工程上解决系统处在动态阶段的问题有一定的指导意义[2]。
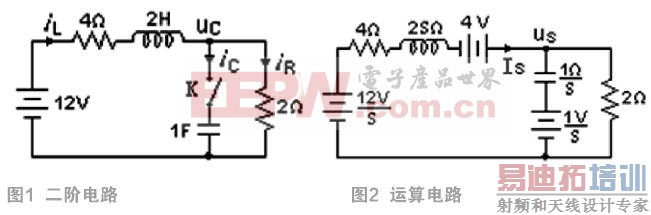
本文以求解图1所示电路的电容电压和电感电流为例,介绍四种基于Matlab的电路动态过程的分析方法。
1 积分法求解状态方程
一个二阶电路如图1所示,开关K原来是打开的,电路已经稳定,uc(0)=1V,il(0)=2A。电源电压及各元件的参数值标示于图中。在t=0时,将开关K闭合,求t≥0时的电容电压uc(t)及电感电流il(t)的变换规律[3]。
积分法求解状态方程:如果一个系统的状态描述方程为:
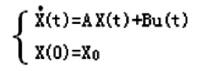
则该系统的状态响应为:
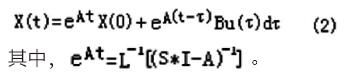
其中。
对于图1所示的电路,以电容电压uc和电感电流il为状态变量,则建立电路的状态方程为:
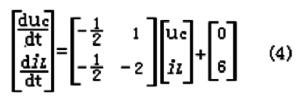
编程求解状态响应uc(t)与il(t):
syms x1 x2 s t z ;
A=[-1/2,1;-1/2,-2]; Bu=[0;6];
X=[x1;x2];X0=[1;2];
Asi=eye(2)*s-A; % s*I-A;
AA=inv(Asi); % [s*I-A]-1;
eAt=ilaplace(AA); %e A t=L-1[([sI-A]-1];
eAtz=subs(eAt,t,t-z); %求eA(t-z);
X= eAt*X0+int(eAtz*Bu,z,0,t); % Bu= B*u(z);
uc=X(1), il=X(2)
运行程序得:
uc = 3*exp(-3/2*t)-6*exp(-t)+4
il = -3*exp(-3/2*t)+3*exp(-t)+2
即电容端电压和电感中电流的解析解为:
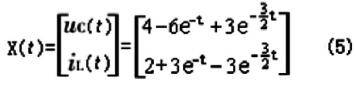
积分法求解电路响应的过程是:以电容电压和电感电流为状态变量建立电路的状态方程;根据状态方程确定矩阵A、B;求矩阵指数eAt;根据方程式(2)求状态变量的解析表达式,最后求出要求电量的解析表达式[4]。
2 用Matlab拉普拉斯变换法求解
时域分析法用于高阶电路的分析计算时,确定初始条件和积分常数非常繁琐。可采用拉普拉斯变换法来求解。将时域电路变换为复频域电路,即运算电路[5]。在运算电路的基础上,用与直流电阻电路相同的方法进行分析,建立s域描述方程。通过对s域方程的运算,得到电路中待求电量的象函数F(s),对象函数F(s)进行拉氏反变换就得到对应的时域解f(t)。
图1对应的运算电路如图2所示,由运算电路得:
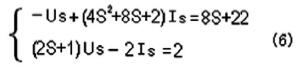
针对方程组(6)进行MATLAB编程:
syms t s;
A=[-1 4*s^2+8*s+2;2*s+1 -2];
B=[8*s+22;2];
AA=inv(A); %A的逆阵;
X=AA*B;
Us=X(1); %电容电压的象函数;
Is=X(2); %电感电流的象函数;
Uc(t)=ilaplace(Us), il(t)=ilaplace(Is)
程序运行结果为:
Uc(t) =3*exp(-3/2*t)-6*exp(-t)+4
Il(t) =-3*exp(-3/2*t)+3*exp(-t)+2
该结果与方法1的结果完全一致,即电容电压uc(t)和电感电流il(t)的解析表达式同式(5)。
3 用ODE函数求微分方程的数值解
基于龙格-库塔法,MATLAB提供了一套求常微分方程数值解的函数,可以根据不同的对象选择不同的算法。其函数格式如下:
[X,Y]=ode23(‘f’,[x0,xn],Y0)
[X,Y]=ode45(‘f’,[x0,xn],Y0)
其中:X,Y是两个相量,X对应自变量x在求解区间[x0, xn]的一组采样点,其采样密度是自适应的,无需指定;Y是与X对应的一组解。f是一个M函数文件,代表待求解方程。[x0,xn]代表自变量的求解区间。Y0=Y(X0),由方程的初值给定。函数在求解区间[x0,xn]内,自动设立采样点向量X,并求出解函数Y在采样点X处的样本值[6]。
本文选用采用了四阶、五阶龙格-库塔法的ode45函数,它采用自适应变步长的求解方法,即当解的变化较慢时,采用较大的步长,从而提高了计算速度;当解的变化较快时,步长会自动地变小,可以提高计算的精确度。
图1的状态方程为式(1),初始条件为:uc(0)=1V,il(0)=2A,MATLAB程序如下:
function dy = myfun (t, y); % 将方程式定义为函数文件并取名存盘以便调用
dy= zeros(2,1); %变量y为两行一列相量
dy(1)= -1/2*y(1)+ y(2);
dy(2)= -1/2*y(1)-2*y(2)+6;
[t,y]= ode45(‘myfun’,[0,10],[1,2]); % 调用ODE函数并代入初始条件
t’; %转置显示自变量的一组采样点
y(:,1)’;y(:,2)’;% 转置显示y(1)、y(2)与采样点对应的一组数值解
uc= y(:,1);
il = y(:,2);
plot(t,uc,’linewidth’,1.5);%绘制uc波形,波形线宽为1.5
grid; set(gcf,’color’,’w’) % 打开网格;使输出图形的背景为白色
axis([0 10 0.8 4.2]); % 设定坐标轴的范围
set(gca,'xtick',[0 2 4 6 8 10]); %设置x轴刻度标示
set(gca,'ytick',[1 2 3 4]); %设置y轴刻度标示
xlabel(‘自变量t /s’) ; % x轴加注释
ylabel(‘因变量uc /v’); % y轴加注释
title(‘uc的波形’); % 图形正上方加注释
figure; %打开第二个图形界面
plot(t,il,’linewidth’,1.5); %绘制il波形,波形线宽为1.5
grid; set(gcf, ‘color’, ’w’);
axis([0 10 1.9 2.5]); %设定坐标轴的范围
set(gca,'xtick',[0 2 4 6 8 10]);
set(gca,'ytick',[2 2.2 2.4]);
xlabel(‘自变量t /s’);
ylabel(‘因变量il /A’);
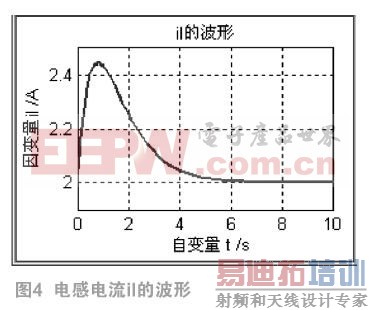
title(‘il的波形’);
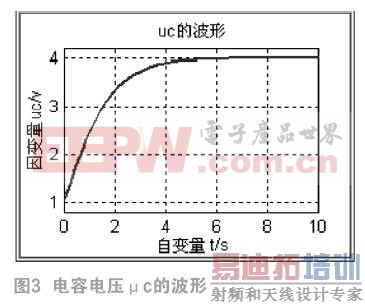
在此,由于篇幅有限,没有显示自变量的采样点和与采样点对应的数值解,而只是将解以图形的方式输出,如图3和图4。从结果看出,用数值积分ODE函数求解状态方程简单方便,易于理解和掌握。与其它语言程序相比,可大大节省编程时间[7]。
4 构建微分方程的simulink模型求解
对于形如y''=ay'+by+c的微分方程,构建simulink模型的核心思想是:y''经过积分得y',y'经过积分得y,而y'、y经过代数运算又可得到y''。由微分方程式(4)得:
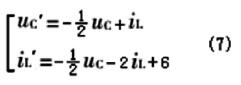
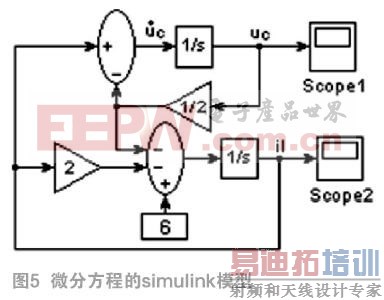
根据式(7),可构建出图5所示的simulink模型。其中用到两个积分模块、两个求和模块、两个比例模块和一个恒定模块。两个示波器用于输出uc和il的图形[8]。
simulink模型建成以后,要对uc和il设置初值:uc(0)=1V,il(0)=2A,双击uc模块将初始值设为1V,双击il模块将初始值设为2A。设置示波器的信号显示范围:scope1,t:0—10s,Y:0.8—4.2;scope2,t:0—10s,Y:1.9—2.5。
开始仿真:选择simulation下的parameter命令,设置仿真的start time为0s,stop time为10s。最后选择simulation下的start命令进行仿真,或击模型窗口工具栏上黑色右三角图标进行仿真。
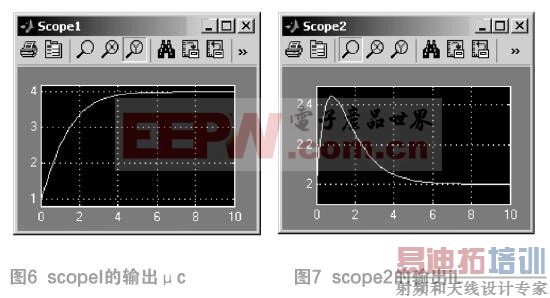
双击示波器scope1和scope2,则会得到图6和图7,与图3和图4的uc和il曲线完全相同,即两种仿真结果一致。
5 结论
通过本文介绍的几种动态电路的分析方法看到:积分法求解动态电路,以电容电压和电感电流为状态变量建立电路的状态方程,根据状态方程求出状态变量的解析表达式;用ODE函数求解微分方程组,对求解动态电路带来了极大方便,并给出了解的直观图形;利用Matlab语言直接进行拉氏变换求解动态电路,大大提高了计算效率;而利用Matlab的Simulink功能得到了一种全新的求解暂态电路的思路。 Matlab的编程效率高、语言简练、绘图方便。运用Matlab可使电路的分析运算变得方便和快捷。运用Matlab语言编程和Simulink仿真的方法对复杂电路进行分析和计算,不仅可以节约计算时间、方便地调试电路参数,还可以通过图形非常直观地观察到其响应的过渡过程[10]。所以Matlab在电路理论学科研究与工程实践中都具有很好的应用价值。
参考文献:
[1] 张洪宝.Matlab在动态电路分析中的应用[J]. 鲁东大学学报, 2009(2):144—147.
[2] 王光亮.用Matlab编程实现动态电路仿真[J].江西电力职业技术学院学报,2007(3):8-10.
[3]杨红权,辜承林.Matlab符号运算在电路分析中的应用[J].电气电子教学学报,2008(1):23-26.
[4]蔡启仲.控制系统计算机辅助设计[M].重庆:重庆大学出版社,2003.8.
[5]邱关源.电路[M].北京:高等教育出版社,1999.
[6]于润伟.Matlab基础及应用[M].北京:机械工业出版社,2003.10.
[7]张颖,甘正佳,金维香.基于Matlab的暂态电路分析与计算[J]. 长沙电力学院学报,2002(3):44-47.
[8]王群, 耿云玲. Simulink在电路分析中应用[J].电力自动化设备, 2007(4):71-75.
[9]陈怀琛.M at lab及在电子信息课程中的应用[M].北京:电子工业出版社,2002.
[10]黄忠霖,黄京.Matlab符号运算及其应用[M].北京:国防工业出版社,2004.
本文来源于中国科技核心期刊《电子产品世界》2016年第11期第59页,欢迎您写论文时引用,并注明出处。
上一篇:基于MSP430的信号发生系统设计
下一篇:降低电源纹波噪声的一些常用方法


