指针式万用电表电阻测量电路的计算和第二误差分析

摘要：提出并论述指针式万用电表电阻测量电路的计算程序及其第二误差(电路设计误差)的概念并加以分析(第一误差已在文献^[1]中论述)。从设计和使用的角度出发出，分析造成误差的原因和减小误差的方法。纠正生产厂家在电阻测量技术规范中的错误概念，提出作者的建议。

导引

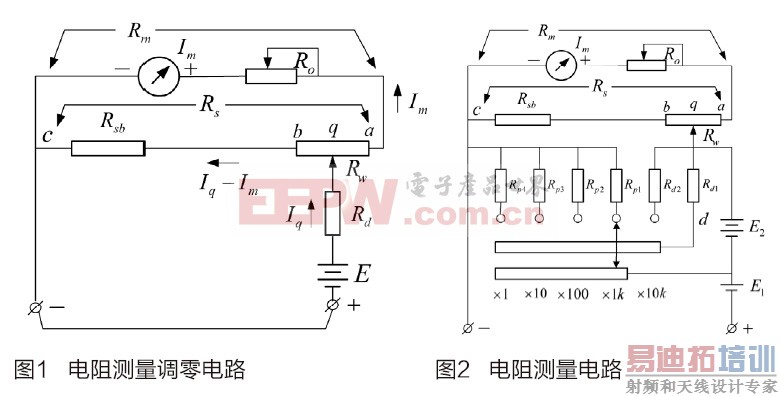
　　图1为电阻测量调零电路。通过表笔将欧姆档的﹢﹣接线端子短接。

　　其中，称I_m为表头灵敏度，R_m为表头支路电阻，R_s为分流电阻，R_w为零欧姆电位器，是分流电阻的一部分，R_d为限流电阻，E为电池。通过调节R_w使表头满度，即为表头电流I_m。此时指针指示电阻值为零欧姆。随着使用电池电压由最高电压E_n，降至标称电压E_q，再至最低电压E_l。欲使表头满度，R_w的滑臂由b点移至q点，再移至a点。电池提供的电流也由I_b降至I_q，再降至I_a。

　　设定R_w的滑臂在某一位置，如 。由图1得到

　　(I_x-I_m)R_sx=I(R_m+R_s-R_sx) 即 I_xR_sx=I_m(R_m+R_s)

　　其中，R_sx为x、c两点之间的电阻值。

　　为了便于计算，又因零欧姆电位器R_w滑臂自b点滑动到a，对综合阻值(限流电阻R_d与表路电阻串联的阻值)影响较小，这便可假定电流I_a或I_q或I_b的数值仅与电池电压E成正比，即I_q/I_a=E_q/E_l和I_b/I_a=E_h/E_l称作“正比关系”。

1　电阻测量电路计算举例

　　该电阻测量电路是采用“标称法”^[2]进行电路布局的，如图2所示。

　　已知：低压干电池E_l的标称电压E_lq=1.5V，最高电压E_1h=1.65V，最低电压E_1l=1.35V，平均内阻r₁=0.0006kΩ。高压叠层电池E₂的标称电压E_2q=9V，最高电压E_2h=9.9V，最低电压E_2l=8.1V ，平均内阻r₂=0.5kΩ。表头灵敏度I_m=0.05mA、表头支路内阻R_m=1.8kΩ。

　　求：倍率为R×10k、R×1k 、R×100、R×10、R×1各档电阻值。

　　计算：为了扩大电阻的测量范围，在R×10k档，高、低压电池E₂和 E₁串联使用。即串联后的标称电压E_q=E_1q+E_2q=1.5+9=10.5V，最高电压E_h=E_1h+E_2h=1.65+9.9=11.55V，最低电压E₁=E_1l+E_2l=1.35+8.1=9.45V，平均内阻r=r₁+r₂=0.0006+0.5=0.5006kΩ。

　　按“标称法”^[2]进行计算，即将计算电池为标称电压E_q时的综合阻值作为中心阻值R_z。

　　设中心阻值 R_z=16.5Ω(刻度值)，在倍率为R×10k档时的中心阻值R_zo=165kΩ。

　　电池在最低电压E_l时，零欧姆电位器R_w的滑臂移至a点，此时流入a点电流

　　下面计算R×1k、 R×10、R×100、 R×1各倍率档的电阻值。这里仅用低压干电池E₁。

　　根据“正比关系”流入q点的电流

2 误差计算

　　校对并通过调整R_w能够满足要求的电池的最低电压E_l,<1l、最高电压E_hh>E_1h。

　　从a、c两点之间看进去的表路电阻值

　　因为“正比关系”是一种近似，故应将R_w增大，为保持R_s不变，即须将R_sb缩小，否则R_w可调的电池最高电压通不过。有R_sbo=0.93R_sb=0.93×10.125=9.41625kΩ

   其中，0.93是人为的调整系数，其数值可通过程序经多次运行结果而定。

　　从b、c点看进去的表路电阻值

　　使用MATLAB语言编制程序，运行结果与本例的手算结果一致。

3 误差分析

　　通过设定不同中心阻值计算结果发现，随着中心阻值的减小相对误差也减小，其量程也减小了，这就需要处理好误差与量程之间的关系。这种误差是在电路设计中自然引入的，也是不可避免的。误差值是随着电池电量的减小由γ_b逐渐变至γ_a，取二者中绝对值最大的一个，称可见，比起第一误差，第二误差是比较小的，因此压低第一误差是主要的。这要从改善表头制作工艺和电阻取值精度上下功夫。

　　作者建议，可以通过选取较低的中心阻值将第二误差压低到忽略不计的程度，在本例中，如设定中心阻值为12Ω，经程序计算得到γ_a=-0.2641%，γ_b=0.0969%，真可以忽略不计了。国内有些厂家的确就是这样做的。另外，生产厂家不应以全程弧长的百分比来定义误差，而应以上述的总误差(第一误差与第二误差之和)来定义。

参考文献：
　　[1] 吕炳仁. 指针式万用电表电阻测量电路的误差分析[J]，北京：电子产品世界，2014(10)
　　[2] 赵宝义. 万用电表[M]，上海：上海人民出版社，1974：65-7
　　[3] 沙占友，王彦明，睢丙东，杜之涛. 万用表速学巧用一本通[M]，北京：中国电力出版社,2012.：27-31
　　[4] 宗建华. 智能电能表[M]，北京：中国电力出版社, 2012