示波器基础--增强分辨率（ERES）

I. 增强分辨率

增强分辨率函数应用有限脉冲响应(FIR)滤波器，其与使用简单的平均滤波器平滑信号类似，但带宽效率更高，拥有更好的带通特点。在平均连续曲线具有重要意义。 对于信号拥有单次特点(信号不能重复，或不能设置稳定触发)而不能使用平均函数时，可以使用这一函数。

a. 增强分辨率的优势

增强分辨率(ERES)滤波改善了仪器具有两个特点：

1. 在任何情况下，每个滤波器使用固定数量都会改善分辨率(即区分相距很近的电压电平的能力)。不管信号是否有噪声，是单次信号还是重复信号，这都可以有效提高分辨率。

2. 可以改善信噪比(SNR)，具体取决于原始信号中的噪声形式，因为增强分辨率滤波会降低信号带宽，进而滤除部分噪声。

b. 力科示波器中的增强分辨率

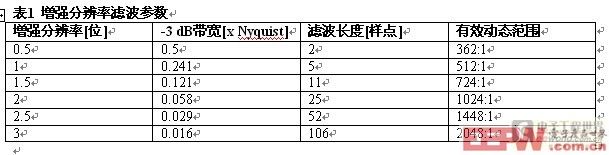
力科DSO实现了一套线性相位有限脉冲响应(FIR)滤波器，这些滤波器是为提供快速计算、完美的阶跃响应、及以0.5位步长在0.5-3位之间改善分辨率、同时使带宽下降最小而优化的。每个0.5位步长对应两倍的带宽下降，可以简便地控制带宽/分辨率之间的矛盾。下表是这些示波器中提供的六种滤波器的参数。

使用的滤波器是低通滤波器，因此在具体情况下SNR的实际提高程度取决于信号上存在的噪声的功率谱密度。如果信号中的噪声是白噪声，即均匀分布在频谱中，滤波器改善SNR的程度与其改善分辨率的程度相同。如果噪声功率偏向高频，那么SNR改善程度将好于分辨率改善程度。如果噪声主要分布在较低的频率上，那么SNR改善程度可能会低于分辨率改善程度。由于去掉相干噪声信号而改善SNR的程度(如时钟信号馈通)取决于信号是否位于滤波器的传输频带中。通过使用数字示波器的频谱分析选项，可以简便地导出结果。 [p]

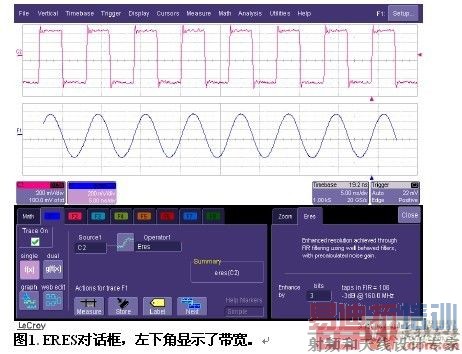
增强分辨率对话框(参见图1)可以协助用户为具体应用选择适当的滤波器，表明ERES滤波器的-3 dB带宽是与当前波形的当前时基设置对应的实际频率。

增强分辨率函数使用的滤波器拥有完全线性相位响应，它有两个所需的属性：第一，滤波器不会使波形中不同事件的相对位置失真，即使事件的频率成分不同。第二，在计算滤波的波形过程中，可以完全补偿与滤波有关的正常延迟(输入波形和输出波形之间)。

II. 什么时候应该使用增强分辨率？

特别适合增强分辨率的主要情况有两种：第一，如果信号的噪声明显很高(且不要求测量噪声)，那么可以使用增强分辨率函数“清除”信号。第二，即使信号噪声不太高，但要求对波形进行高精度测量(可能在高垂直增益的情况下使用缩放)，那么增强分辨率将提高测量的分辨率。

从整体上看，在数据记录具有单次特点或低速重复特点、不能使用平均函数的情况下，增强分辨率可以代替平均函数。

下面的实例介绍了在这些情况下使用增强分辨率函数。

III. 滤除噪声

图2显示了增强分辨率对有噪声的信号的影响，上图显示的是带有噪声的阻尼正弦曲线。下图显示了在3位分辨率增强后的同一信号。现在可以清楚地看到较低电平的振荡，可以对感兴趣的信号进行频率、幅度或周期等测量。在频域中查看的同一信号显示了增强分辨率函数的低通滤波影响。图3显示了图2中的信号的功率谱。上面的一对曲线显示了输入波形和没有滤波的信号的频谱，下面的一对曲线则显示了3位分辨率增强后的信号和信号频谱。3.0位增强滤波器拥有200 kHz的-3 dB带宽。在超过这个频率时，滤波器从信号中去掉能量。

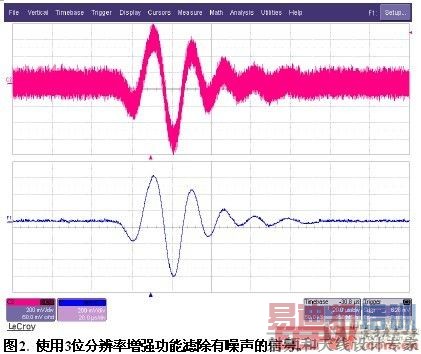
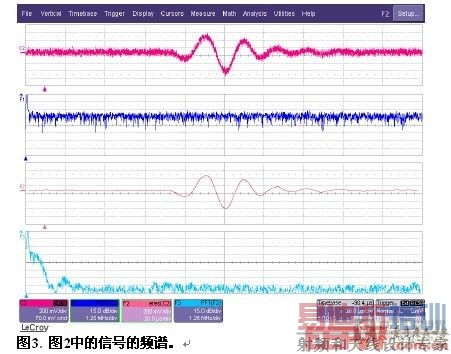
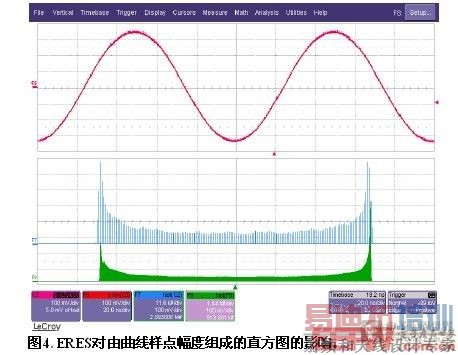
图4是增强分辨率的另一个工作视图。我们考察了采集的正弦波及进行3位增强分辨率处理后正弦波的直方图。上面的直方图表示通道2中的波形每个样点的电压幅度。这是8位数据，在使用显示的2000个二元组绘制直方图时，由于8位数字化器的分辨率有限，显示了象鸡冠一样的外观。 [p]

下面的直方图是经过增强分辨率处理后的同一波形。注意，每个二元组包含着数据，表明现在有超过2048个电压电平(11位)。

IV. 改善带宽

在许多应用中，带宽损失可能会限制增强分辨率的用处。在这些情况下，可以使用增强分辨率，改善波形分辨率，而不是信噪比。可以通过两种方式校正带宽限制。如果信号是重复的，那么可以使用随机通道复用采样或RIS。在RIS模式下，示波器对重复波形的有效采样率提高到高达200 GS/s。由于增强分辨率带宽与采样频率成比例，因此这可以把处理的带宽提高达10:1。

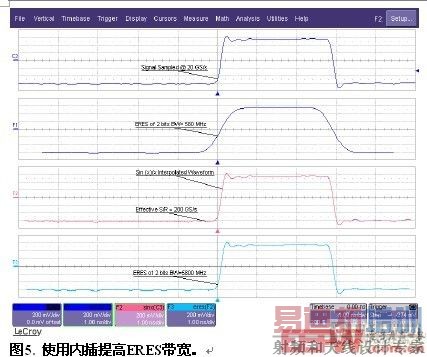
另一种常用技术是对采集的信号应用内插。(Sinx)/x内插函数使有效采样率提高了10:1。选配的内插数学函数可以把有效采样率提高达50:1。在图5中，上面的一对曲线显示了以20 GS/s采样的波形。2位的增强分辨率把带宽降低到580 MHz。通过应用(sinx)/x内插，有效采样率提高到200 GS/s，2位增强的增强分辨率带宽现在是5800 MHz。

注意事项

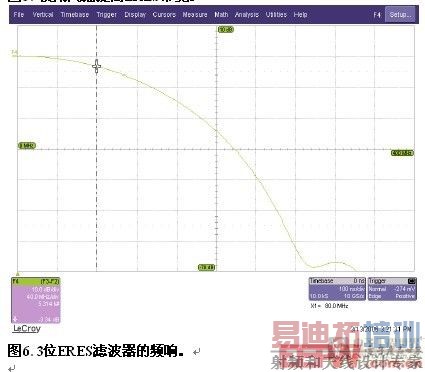
增强分辨率函数只会改善曲线的分辨率，不会改善8位ADC原始量化的精度或线性度。高分辨率滤波器具有良好临时响应的限制，不能使用最大平坦滤波器。因此，传输频带会导致截止频率附近的信号发生小的衰减。所以，在使用这些滤波器时，一定要注意通过的最高频率可能会略微衰减。图6是典型高分辨率滤波器的频响(3位增强滤波器)，其中标出了80 MHz的-3 dB截止频率或1.6%的Nyquist频率。 [p]

必须在有限记录长度上执行滤波。记录末端有不连续点，因为没有定义这些点上的滤波输出。数字示波器没有显示这些数据点，因此在滤波后曲线变得略短。丢失的样点与使用的滤波器的脉冲响应长度完全相同，因此在2 – 106个样点之间变化(参见表1)。由于这里介绍的示波器有非常长的波形存储器，因此通常注意不到这种丢失(在最坏情况下，其只占50,000点曲线的0.2%)。但是，用户可能会要求滤波很短、没有数据输出的记录。在这种情况下，DSO将不允许使用滤波。

VI. 总结

第III部分和第IV部分的实例分别说明了增强分辨率函数的功能：一个降低噪声和低通滤波，另一个是改善垂直分辨率。但在许多情况下，这两种功能是共存的，其会以与平均函数非常类似的方式对得到的增强分辨率曲线产生综合影响。因此，在单次应用中，增强分辨率为替代平均函数提供了理想的方案。