相移干涉技术在小角度及直线度测量中的应用

　　1　引言

　　直线度测量在加工设备、检测设备安装调试过程中起着十分重要的作用,其测量值准确与否将直接影响加工设备的制造精度及检测设备的测量精度。在某些高精度应用场合,直线度测量数据直接参与加工及测量设备的精度补偿,是精度补偿过程的数据来源,其测量精度决定了仪器设备的使用精度。直线度一般可通过专用仪器(如HP双频激光干涉仪结合直线度测量附件Wollaston棱镜和二面角反射镜)[1]直接测量得到,也可通过使用小角度测量装置(如702光电自准直仪)经换算得到[2]。由于小角度测量装置应用广泛,因而后者成为直线度测量的常用方法。

　　一般小角度测量的原理如图1所示:

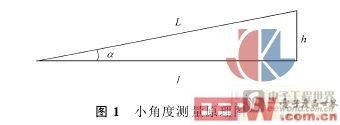
　　其测量方程式可表示为:

　　由于角度很小,上式可写为:

　　这样在L或l确定的情况下,通过测量h即可得到角度α。目前利用自准直仪测量小角度值时,h的测量精度受测微目镜等元件的精度影响,测量精度一般δα≥1″[2]。利用光干涉原理测量小角度有双参考镜方法[3],其核心为一Twyman-Green干涉仪。应用这一方法进行测量时,条纹间隔提供的灵敏度是精确读取间隔值尾数的关键,由于条纹亮度、形状很不一致,要想获得高精度的检测结果是不可能的[4]。同时受双参考镜夹角取值范围等条件影响,双参考镜小角度测量的误差δα≥0·5″[3]。

　　在进行直线度测量时,需要对两个方向(俯仰和偏摆)上小角度的测量才能实现对直线度的测量。采用上述两种测量方法时,不可能同时获得两个方向上的小角度值。然而本文所提出的,利用相移干涉技术结合Zernike波面拟合技术的测量方法,不但能够同时获得正交两个方向上的小角度值,而且可使测量精度和测量速度得到大幅度的提高。

　　2　小角度相移激光干涉测量原理

　　利用相移干涉技术测量小角度的原理如图2所示:

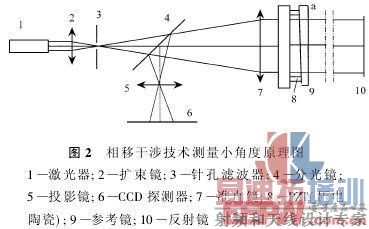
　　如图2,激光器1发出稳频激光经扩束镜2扩束、针孔3空间滤波后得到高质量的球面波,经准直镜7、参考镜9作用后,一束光经参考镜标准面a反射得到参数波面,另一束透射光经反射镜10反射形成被检波面,两束光经分光镜4和投影镜5作用后在CCD探测器6的像面上产生干涉条纹。所谓相移干涉技术,是通过PZT对光程差的调制在时间域中实现相位调制的干涉技术[1]。图2中,参考镜9是在PZT 8的作用下实现对参考波面和被检波面之间光程差的调制。得到被检波面的初始相位后即可得到反射镜10的面形误差、反射镜10和参考面a的空间角度。这里的空间角度就是我们所要测量的小角度值。反射镜10的初始相位可通过下面的四步算法得到[1]。

　　得到反射镜上各点的初始相位后,即可通过下式得到对应点相对于参考面的光程差:

　　OPD(x,y)中包含了反射镜的面形误差信息及反射镜的倾斜信息,这里的倾斜量就是我们感兴趣的小角度信息。正交x、y方向上的倾斜量也就是在直线度测量中我们所要测量的俯仰角和偏摆角,x、y两方向上的倾斜量可通过Zernike多项式波面拟合技术计算求解。

　　3　小角度Zernike波面拟合求解

　　由于光学表面趋于光滑连续,因此它可以表示成一个完备基底函数系的线性组合或一线性无关的基底函数系的组合。在光学检验中,Zernike正交多项式通常被用来作为基底多项式表示被检波面波像差[5]:

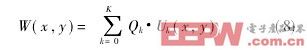
式中:W(x,y)为波像差,Qk为Zernike系数,Q为系数Qk组成的列向量,U为Zernike多项式的项Uk组成的列向量,K为多项式的项数。

　　Zernike多项式的前6项可表示为:

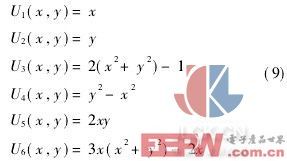
　　由此可以看出式(9)前两项为倾斜项,它们所对应的系数就是x、y方向上被测小角度的正切值。Zernike多项式的系数可通过CCD上各像元点所对应的光程差利用最小二乘法求解得到,但由于Zernike多项式是在连续域上正交的,而我们所测得的数据是离散的,这样直接利用式(8)计算会有很大的不便。为解决这一问题,人们提出了Gram-Schmidt正交化算法,求出一组在所测数据点上离散正交的、且为Zernike多项式线性组合的基底函数系V,得

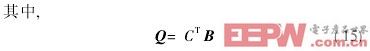
　　在式(14)的基础上,利用最小二乘法及V矩阵的正交性可以求出系数向量B,再经过式(15)变换可求出系数向量Q。

　　实际在小角度、直线度的检测中,我们只需求得Zernike多项式中倾斜项的系数即可。需要注意的是,以上我们所求解的是反射波面的Zernike多项式系数,而它与反射镜面形误差之间为两倍关系,即:

[p]

　　4　导轨直线度测量实验

　　直线度误差与角度变化的关系如下式:

　　其中,L为板桥跨度,即测角采样长度。根据上述原理,我们应用Zygo GPI数字波面干涉仪对一根行程1 m的滚珠直线导轨进行了检测。测量结果如表1所示。

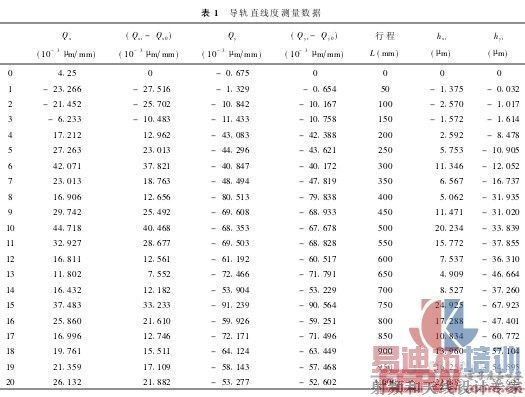
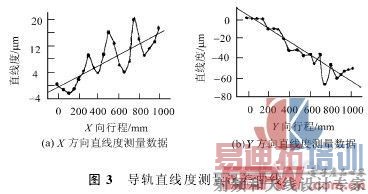
　　利用表1中的数据得到导轨两方向直线度误差曲线如图3所示,并利用最小二乘法对其拟合。对X方向直线度测量数据进行线性拟合,得到:

　　按照拟合直线的斜率对原始数据进行坐标旋转,得到去掉倾斜值的直线度误差数据,根据式(24)最终计算得到导轨X方向的直线度18·014μm,Y方向的直线度32·327μm。

　　5　精度分析

　　由于相移干涉仪所使用CCD的像元数为512×512,这样系统的分辨率为λ/512。当反射镜与参考镜的口径相同均为100 mm时,转换到角度测量分辨率为λ/(512×100),其中λ=0·632 8μm。在小角度测量时,tanα等于后次测量的倾斜系数减去前次测量的倾斜系数,而倾斜系数表示的是反射镜与参考镜之间的相对位置关系,与参数镜和反射镜本身的面形精度无关。这样,利用相移干涉技术的小角度测量精度只与干涉仪的重复测量精度有关,本实验中所使用干涉仪的重复测量精度优于λ/100,转换成角度测量精度为λ/(100×100)。

　　6　结论

　　本文利用相移激光干涉仪结合Zernike波面拟合技术对小角度的测量进行了探讨和研究,证明该方法用于小角度和直线度测量时,与一般方法相比,能大大提高测量分辨率和测量精度,为小角度和直线度的高精度测量提供了一条新的途径。

　　参考文献

　　[1]　金国藩,李景镇.激光测量学[M].北京:科学出版社,1998,683-684.

　　[2]　王之江等.光学技术手册[M].北京:机械工业出版社,1994,1118-1123.

　　[3]　朱鸿锡等.新型高精度激光干涉小角度测量仪的研究[J].计量学报,1996,17(2):89-91.

　　[4]　和田尚等.用外差莫尔条纹法对直线性的检测[J].精密机械.1985,51(6):100-107.

　　[5]　Malacara D. Optical Shop Testing[M]. New York: JohnWiley, 1978.