- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
四点测球法在球坑自动检测中的应用
1 引言
在在线、自动检测系统中,球坑的测量一般采用包容法。而在需精确测得球坑半径的数值时,包容法显然不能满足要求。为此,需要探索既能满足要求而又简单实用的方案。本文在分析了四点测球法理论模型的基础上,提出了两种不同的四点测球方案,通过分析、比较,最后确定出实际测量方案。
2 四点测球法理论最优方案
空间要确定一个球,必须有四个参数,即球心坐标(a,b,c)和球半径R。对应地要已知球面上四个点的坐标才能建立四个方程,构成一个方程组。因此,为了实现球参数的测量,至少要建立四个测量点,即所谓四点测球法。


由于任何测量系统都存在误差,所以由实测的四点Pi得到的球半径存在测量误差δR。设x,y,z三个方向上的测量误差均为±Δ,根据误差理论有:
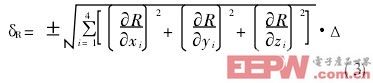
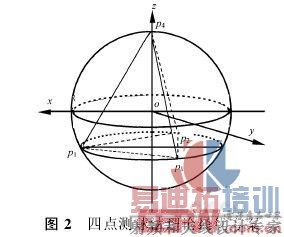
由式(3)可知,球半径的测量误差与各点坐标测量误差有关,可以通过合理布置测量点的位置,使球半径测量误差达到最小,即存在最优方案。理论分析表明,若被测球为标准球,当Pi(i=1,2,3,4)四点在空间构成正四棱锥时,测得的球半径误差最小[1],如图2所示。此时,δR=±Δ/2。
3 球坑测量方案的讨论
3·1 “三加一”方案
测量对象为半球坑,图2的方案显然不可能实现。但受其启发,可采用3+1的形式,即三个测点Ⅰ、Ⅱ、Ⅲ布置在同一圆截面上且互成120°另一个测点Ⅳ布置在球顶点。如图3所示,称之为“三加一”方案。 [p]
可以设想,测量时,由1、2、3、4组成的测杆机构在气缸的推动下向下推进,直到死挡块限位时为止。设测杆中心O的坐标为(0,0,0),并以它作为坐标原点,计算对应的被测球的球心P的坐标(a,b,c)和球半径R。设测点Ⅰ、Ⅱ、Ⅲ、Ⅳ到O点的距离分别为r1、r2、r3、r4。则在如图的坐标系中,Ⅰ、Ⅱ、Ⅲ、Ⅳ的坐标分别为:
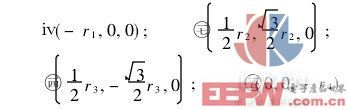
将以上各点坐标代入式(1)、式(2),解方程组可得a,b,c,R的值。由于被测球坑采用成形铣刀加工,该球坑“赤道平面”附近区域加工质量好,而在“极地”附近区域加工质量较差。因此,该方案中测点Ⅳ的选择就不太理想。
同时,在确定各测点坐标时,是采用测头的相对位移加上原来各测点到O点的绝对长度得到的(见图3)。O点是测头4所在轴线与测头1、2、3所在平面的交点。而要精确测出各测头到O点的绝对长度也是比较困难的,尤其当被测球坑半径较小时更难实现。
3·2 “二加二”方案
通过对“三加一”方案的讨论,针对其不足,引发出“二加二”方案[2]。该方案将四个测点布置成二二对称的2+2形式,并使两组测点分别位于不同的水平面上,如图4所示。测点1和2同在一个平行于“赤道平面”的圆截面上,3和4在另外一个圆截面上。图中虚线所示为各测头球心的轨迹,由于测量时保证各测点均与球内壁相接触,当测头半径为r时,被测球面与各测头球心的轨迹是两个半径差为r的同心球面。于是,对被测球面的测量就转化为对各测头球心轨迹的测量。同样根据四点测球原理,只要测得与球内壁接触的四测头的球心坐标,那么代入式(1)和式(2),即可计算出被测球坑的参数a、b、c、R。
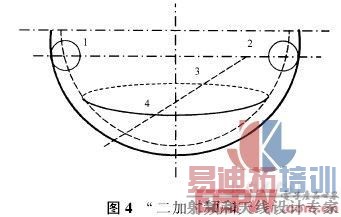
与前一方案相比,“二加二”方案明显克服了“三加一”方案的不足之处。首先,测点选择避开了加工质量较差的极地区域,从而避免了由加工质量引起的测量误差。同时,采用对径测量,还可以消除偏心和抖动的影响。通过分析、比较,对于所讨论的检测对象,决定采用“二加二”方案。
4 方案的实施与应用
从前面的分析可知,“三加一”方案不适合作者拟检测的对象。事实上,由于待测球坑尺寸的限制(SR=7·15 mm),采用该方案时测头的空间布置也几无可能。当然,采用“二加二”方案,在测头的空间布置上也同样存在困难,需要缜密考虑、精心设计。
作者采用沿z方向放置的高精度电感式位移传感器来感受位移的变化,球面坐标的变化到z向位移的转换通过灵敏杠杆的预变换来实现。四个灵敏杠杆前端的测点布置成二二对称的形式,并使两组测点在z向错开,建立在不同高度的水平面内。这样,最终构成的四点测球坑传感器外径被限制在43 mm的范围内,4个测头从端部伸出可探入SR7·15 mm的半球坑。其中杠杆1、2位于yoz平面内,杠杆3、4位于xoz平面内,如图5所示。图中li(i=1,2,…,16)表示杠杆的结构尺寸,si(i=1,2,3,4)表示测量球坑参数时各个传感器的示值,ai(i=1,2,3,4)表示杠杆与水平位置的夹角。
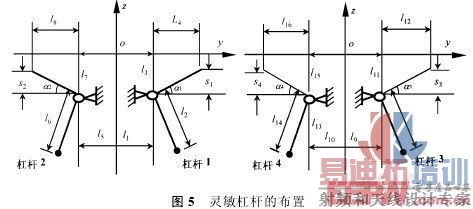
各测点对应的空间坐标为(xi,yi,zi),(i=1,2,3,4)。根据几何关系,各测点坐标与传感器示值、杠杆结构尺寸及空间位置之间构成下列关系:
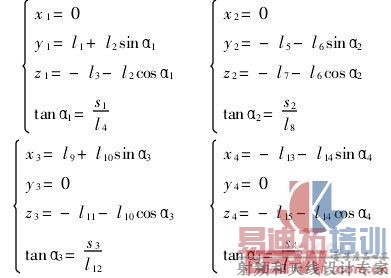
据此求出xi、yi、zi(i=1,2,3,4)后,代入式
(1)、式(2)即可求得球坑参数。
根据上述原理设计的四点测球坑传感器已用于自动测量仪中。对该传感器进行误差分析(另文发表),其球坑测量的理论不确定度为δR=±0·9μm。采用SR7·146 mm的标准球坑进行校准,经10次测量,得球坑半径的极限误差δlimR=±1μm,与理论计算吻合。
参考文献
[1] 张国雄,张德芬.四点法测量球心和球半径的最优方案[J].计量学报, 1993,14(4):247-250.
[2] 丁鸣忠.汽车空调压缩机活塞零件在线综合测试系统研究[D].上海:上海交通大学仪器工程系,1995.
上一篇:超声波料位仪的研制
下一篇:相移干涉技术在小角度及直线度测量中的应用


