利用NI LabVIEW优化多核处理器环境下的自动化测试

多线程编程的挑战

迄今为止，处理器技术的创新为我们带来了配有工作于更高时钟速率的CPU的计算机。然而，随着时钟速率逼近其理论上的物理极限，人们开始投入到具备多个处理核的新型处理器的开发。借助这些新型多核处理器，工程师们在自动化测试应用开发中利用并行编程技术，可以实现最佳的性能和最大的吞吐量。爱德华×李博士——加州大学伯克利分校电气与计算机工程教授——阐述了并行处理的技术优势。

“许多技术专家预言，对于摩尔定律的终结回应，将是日趋并行的计算机架构。如果我们希望继续提高计算性能，计算机程序必须能够利用这种并行机制。”

而且，业界专家业已认识到，对于编程应用，如何利用多核处理器将是一个巨大的挑战。比尔×盖茨——微软公司的缔造者——是这样论述的：

“要想充分利用并行工作的处理器的威力，…软件必须能够处理并发性问题。但正如任何一位编写过多线程代码的开发者告诉你的那样，这是编程领域最艰巨的任务之一。”

幸运的是，NI LabVIEW软件，通过一个直观的、用于创建并行算法的API，为我们提供了一个理想的多核处理器编程环境，所创建的并行算法可以将多个线程动态分配至一

项给定的应用。事实上，您可以利用多核处理器优化自动化测试应用，以获取最佳性能。

而且， PXI Express的模块化仪器增强了这一技术优势，因为这些仪器利用了PCI Express总线所能支持的高数据传输速率。得益于多核处理器和PXI Express仪器的两个具体应用是：多通道信号分析和在线处理(硬件在环)。在此白皮书中，我们将评估各种并行编程技术，并描述每项技术所带来的性能优势。

实现并行测试算法

一项常见的得益于并行处理的自动化测试应用便是多通道信号分析。由于频率分析是一项占用处理器运行时间较多的操作，您可以并行运行测试代码，将每个通道的信号处理分配至多个处理器核，提高执行速度。从编程人员的角度来看，为获得这一技术优势，唯一需要改变的只是测试算法结构的细微调整。

为描述这一过程，现比较用于多通道频率分析(快速傅立叶变换或FFT)的两个算法的执行时间，它们分别位于一个高速数字化仪的两个通道上。NI PXIe-5122 14-位高速数字化仪的两个通道均以最高采样率(100 MS/s)采集信号。首先，我们察看LabVIEW中对应于这一操作的传统顺序编程模型。

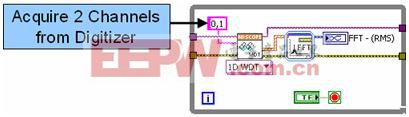
图1. 利用顺序执行的LabVIEW代码

采集来自数字化仪的两个通道的信号

图1中，两个通道的频率分析均在一个FFT快速VI中完成，它顺序分析每个通道信号。虽然上述算法也可以在多核处理器环境下有效执行，但是，您还可以通过并行处理每个通道来进一步提高算法性能。

如果您剖析上述算法，就会发现完成FFT所需的时间要比从高速数字化仪采集数据长得多。通过每次获取各个通道的数据并且并行执行各个通道的FFT，可以显著降低处理时间。图2表示了一个采用并行方法的新的LabVIEW模块框图。

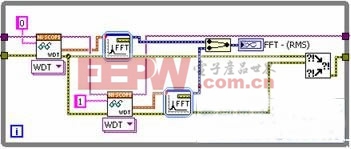
图2. 利用并行执行的LabVIEW代码

顺序获取数字化仪的每个通道的数据。值得注意的是如果两次数据获取均来自不同的仪器，那么您可以彻底并行完成这些操作。然而，由于FFT占用大量的处理器时间，您仍可以仅通过将信号并行处理来改善性能，减少了总的执行时间。图3显示了两种实现的执行时间：

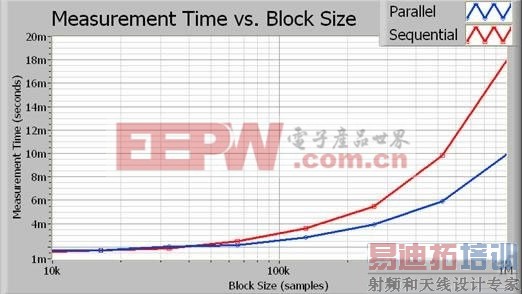
图3. 随着数据块大小的增加，通过并行处理节约的处理时间愈为显著。

事实上，对于更大的数据块，并行算法方法实现了近2倍的性能改进。图4描述了性能随采集数据块大小(以采样数为单位)增大而提高的精确百分比。

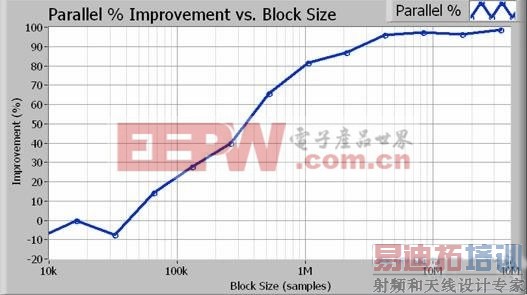
图4. 对于大于1百万采样(100 Hz精度带宽)的数据块，并行方式实现了80%或更高的性能增长。

在多核处理器环境下，可以方便地实现自动化测试应用的性能改进，因为您可以使用LabVIEW动态地分配每一个线程。事实上，您不需要创建特殊的代码以支持多线程，而是通过最少的编程调整，利用多核处理器来达到并行测试。

配置定制的并行测试算法

并行信号处理算法帮助LabVIEW在多个处理器核中划分处理器的用途。图5按顺序描述了CPU处理算法每一部分。

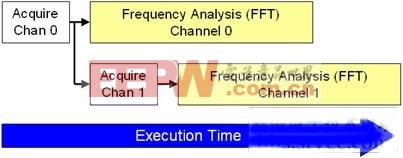
图5. LabVIEW能够并行处理许多采集数据，从而节省了执行时间。

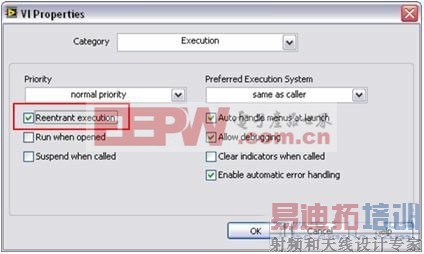
并行处理要求LabVIEW拷贝(或克隆)每个信号处理子例程。缺省情况下，LabVIEW的许多信号处理算法配置为“可重入执行”。这就意味着LabVIEW将动态分配给每个子例程唯一的实例，包括独立线程和存储空间。因而，您必须将定制的子例程的配置，工作于可重入方式。您可以通过LabVIEW中一个简单的配置步骤完成这一工作。欲设置这一属性，选择文件菜单下VI属性并选中“执行”栏;然后，选中“可重入执行”标记(如图6所示)。

[p]

图6. 通过这一简单步骤，您可以并行执行多个定制的子例程，就如同标准的LabVIEW分析函数。

因此，在多核处理器环境下，您可以通过简单的编程技术实现您的自动化测试应用的性能改进。

优化硬件在环应用

得益于并行信号处理技术的又一个应用便是为同时输入与输出使用多个仪器。一般，这些应用被称为硬件在环(HIL)或在线处理应用。在此情况下，您可以使用高速数字化仪或高速数字I/O模块来采集信号。在您的软件中执行数字信号处理算法。最后，通过另一个模块化仪器生成结果。图7描述了一个典型的模块框图。

图7. 该框图描述了一个典型的硬件在环(HIL)应用所包括的执行步骤。

常见HIL应用包括在线数字信号处理(如滤波、插值等)、传感器仿真和定制组件模拟。您可以使用多种技术，以获得在线数字信号处理应用的最佳吞吐量。

通常，您可以使用两种基本的编程结构，单循环结构和带有队列的流水线式多循环结构。单循环结构实现简单，对于小数据块具有较低时延。相比之下，多循环结构能够支持高得多的吞吐量，因为它们能够更好地利用多核处理器。

对于传统的单循环方式，您顺次组织一个高速数字化仪的读函数、信

号处理算法和高速数字I/O的写函数。如图8的模块框图所示，这些子例程中的每一个都必须按照LabVIEW编程模型所确定的顺序执行。

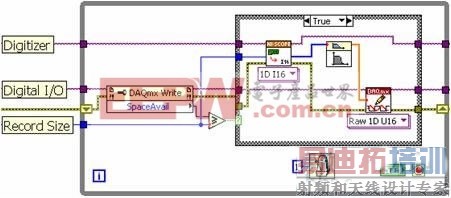
图8. 对于LabVIEW的单循环方式，每个子例程都必须顺次执行。

单循环结构受限于几个因素。由于顺序执行每一环节，处理器在处理数据的同时受限，无法执行仪器I/O。在这种方式下，由于处理器一次只能执行一个函数，所以您无法有效利用一个多核CPU。虽然单循环结构可以处理较低的采集速率，但是，如需更高的数据吞吐量，仍须采用多循环方式。

多循环架构使用队列结构实现while循环间的数据传递。图9描述了多个while循环(带有一个队列结构)间的编程方式。

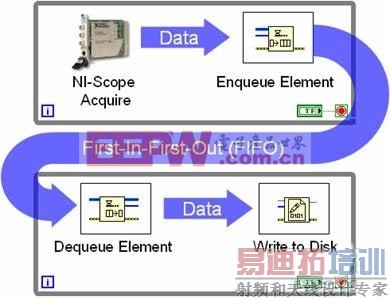
图9. 借助队列结构，可以实现多个循环间的数据共享。

图9所表示的是典型的所谓生产者/消费者循环结构。在此例中，一个高速数字化仪在一个循环中持续采集数据，并在每次迭代中将新的数据集传递至FIFO队列。消费者循环仅需监视队列的状态，当每个数据集可用时将其写入磁盘。采用队列的意义在于这两个循环均可相互独立执行。在上例中，高速数字化仪可以持续采集数据，即使这些数据写入磁盘时存在一定的延迟。与此同时，其它的采样仅需存储在FIFO队列中。通常来说，生产者/消费者流水线方法，通过更有效的处理器利用率，提供更高的数据吞吐量。这一技术优势在多核处理器环境下更为显著，因为LabVIEW可以动态分配处理器线程至每个处理器核。

对于一项在线信号处理应用，您可以使用三个独立的while循环和两个队列结构，实现其间的数据传递。在此应用情况下，一个循环将从一台仪器采集数据，一个循环将专门执行信号处理，而第三个循环将数据写入到另一台仪器。

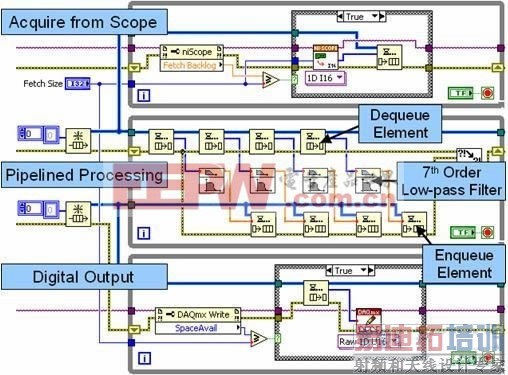
图10. 该模块框图描述了带有多个循环与队列结构的流水线式信号处理。

图10中，最上面的循环是一个生产者循环，它从一个高速数字化仪采集数据，并将其传递至第一个队列结构(FIFO)。中间的循环同时作为生产者和消费者工作。每次迭代中，它从队列结构中接收(消费)若干个数据集，并以流水线的方式独立对其进行处理。这种流水线方式通过支持高达四个数据集的独立处理，实现了在多核处理器环境下的性能改进。注意，中间的循环同时也作为一个生产者工作，将处理后的数据传递至第二个队列结构。最后，最下面的循环将处理后的数据写入至高速数字I/O模块。

并行处理算法改善了多核CPU的处理器利用率。事实上，总吞吐量取决于两个因素，处理器利用率和总线传输速度。通常，CPU和数据总线在处理大数据块时工作效率最高。而且，我们可以进一步使用具有更快传输速度的PXI Express仪器，减小数据传输时间。

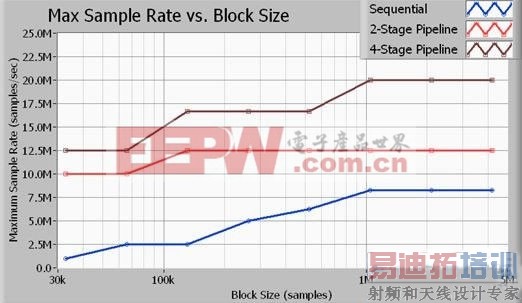
图11. 多循环结构提供比单循环结构高得多的吞吐量。

图11描述了最大吞吐量和采样率的关系，采样数据块大小以采样点数来计算。此处所描述的所有标定都是围绕16位采样进行的。此外，所采用的信号处理算法为一个截止频率为采样率的0.45倍的7阶巴特沃兹低通滤波器。如数据显示，您可以在4阶流水线式(多循环)方式下达到最大数据吞吐量。注意，2阶信号处理方式获得了比单循环方式(顺序)更好的性能，但其CPU的利用率低于4阶方式。上面所列的采样率均为NI PXIe-5122高速数字化仪和NI PXIe-6537高速数字I/O模块的输入和输出的最大采样率。注意，当采样率为20 MS/s时，应用总线的输入和输出的数据传输率均为40 MB/s，所以总的总线带宽为80 MB/s。

而且，应当考虑的是，流水线式处理方式在输入与输出之间确实引入了时延。所引入的时延取决于几个因素，包括数据块的大小和采样率。下面的表1和表2比较了单循环和4阶多循环架构中的实测时延随数据块大小和最大采样率的变化情况。

表1和2. 这两个表格描述了单循环和4阶流水线的时延。[p]