基于灰色Verhulst-小波神经网络的装备故障预测研究

　　李静雯, 杨善红

　　(四川理工学院 计算机学院， 四川 自贡643000)

　　摘   要： 针对现代武器装备故障预测样本少、故障预测精度低、维修保障困难等问题，提出一种基于灰色Verhulst-小波神经网络组合模型的装备故障预测方法。该方法综合了灰色Verhulst模型所需样本少的优点和小波神经网络良好的时频局域化性质和学习能力，克服了小样本故障数据在BP神经网络训练中的缺陷。实验结果表明，与相关研究方法比较，所提出方法具有较高的预测精度，对于武器装备故障预测与维修保障具有一定的理论价值和现实意义。

　　关键词： 灰色Verhulst模型；小波神经网络；故障预测；预测精度

　　中图分类号： TP391 文献标识码： A文章编号： 0258-7998(2014)08-0091-03

　　装备故障预测技术是现代军事武器装备数字化技术发展的必然[1]。该技术的目的不是直接消除故障，而是对即将发生的异常状态或故障具有预测的能力，为装备的维修保障提供决策支持，实现自助式维修保障，降低使用和保障费用的目标。然而，现有装备故障预测大多采用单一方法，比如灰色模型[2-3]，神经网络模型[4-5]等，往往难以保证实际预测结果。为提高预测精度，部分学者和工程技术人员也尝试采用灰色模型与神经网络等组合模型[6-7]进行装备故障预测，但是由于BP神经网络容易陷入局部最优的缺陷，也无法满足实际装备的预测精度要求。

　　本文基于组合模型的思想，将灰色模型与小波神经网络相结合，探讨灰色-小波神经网络组合模型在装备故障预测中应用价值，以某航空装备为例，建立了其灰色-小波神经网络组合模型，通过对比实验，考察灰色-小波神经网络组合模型的有效性，以期为装备故障预测研究提供理论参考。

1 灰色Verhulst-小波神经网络组合模型

　　1.1灰色Verhulst模型

　　灰色模型是基于理论框架而形成的一种建模方法[8]，具有所需样本数少，弱化原始数据的随机性等优点。其模型建立步骤如下：

　　设装备的原始非负数据序列为：

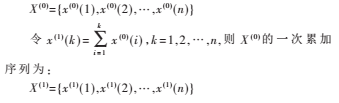
　　令z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)，则X(1)的紧邻均值生成序列为：

　　Z(1)={z(1)(1),z(1)(2),…,z(1)(n)}

　　则灰色模型的基本形式为：

　　x(0)(k)+az(1)(k)=b(z(1)(k))2  (1)

　　对应的白化方程为：

　　采用最小二乘法求解该模型,得到时间响应序列为：

　　1.2 小波神经网络结构及学习算法

　　本文用于装备故障预测的小波神经网络的结构如图1所示。

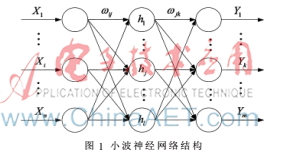
　　该小波神经网络结构是一个三层前馈网络，其中：n为输入层节点数，i=1,2,…,n；l为隐含层节点数，j=1,2,…,l；m为输出层节点个数，k=1,2,…, m； 棕ij为输入层与隐含层之间的权值； 棕jk为隐含层与输出层之间的权值，hj为小波基函数。本文在装备故障预测研究中采用的基小波是国内外常用的Morlet小波，即：

　　在输入数据序列为Xi(i=1,2,…,n)时，则隐含层的输出计算式为：

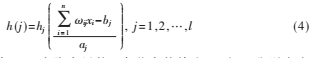
　　其中，h(j)为隐含层第j个节点的输出；aj和bj分别为小波基函数hj的伸缩因子和平移因子。

　　小波神经网络输出层的计算式为：

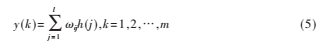
　　本文采用梯度修正法来调整网络的权值和小波基函数的参数，具体调整过程如下：

　　计算机网络预测误差为：

　　其中，yn(k)为模型的期望输出；y(k)为模型的预测输出。

　　根据预测误差e调整网络的权值和小波基函数的参数为：

　　其中， 浊为学习速率。

　　小波神经网络的学习算法的具体步骤如下：

　　(1)网络初始化。赋予ij、ik、aj和bj相应的随机初始值，设置学习速率。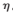

　　(2) 样本分类为训练样本和测试样本，分别用以训练网络和测试网络预测精度。

　　(3) 预测输出。根据输入样本，计算网络输出，并计算预测误差e。

　　(4) 网络的权值调整。根据预测误差e调整网络的权值和小波基函数的参数。

　　(5) 终止规则。判断算法是否结束，如未结束，返回步骤(3)。

　　1.3 组合模型

　　灰色系统具有只需要贫信息和小样本的优势，小波神经网络兼具小波分析技术与人工神经网络技术的优点，使得其具有灵活的函数逼近能力和较好的容错性能。本文尝试将灰色模型和小波神经网络方法进行结合，用于装备的故障预测研究。构建的灰色-小波神经网络组合模型的结构如图2所示。

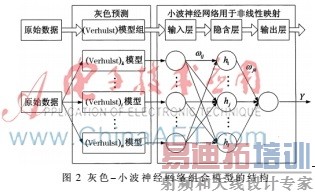
　　灰色-小波神经网络组合模型预测的具体实施步骤如下：

　　(1) 输入装备原始数据序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)}和灰色Verhulst模型所需的最小数据个数k。

　　(3) 采用小波神经网络进行训练。以向量XWNN(t)作为小波神经网络的输入样本，以x(0)(t),t=1,2,…,n作为期望，直到训练达到设置的训练精度为止。

　　(4) 采用灰色-小波神经网络组合模型进行预测。用模型组的预测向量XWNN(t)耦合成小波神经网络的输入，用步骤(3)中的小波神经网络进行仿真，可以得到原始数据的预测值。

2 实例分析

　　为考察本文方法的有效性，选用参考文献[6]中的应用实例(某航空设备工作电压故障预测)，将本文方法的预测结果与参考文献[6]方法及BP神经网络方法对比，验证本文方法的先进性。

　　某航空设备工作电压范围为17~24 V，从0计时，监测间隔为25 h，选择15个电压值作为样本数据，其中前12个数据作为训练样本，后3个数据作为测试样本。在Matlab 2012a软件环境下[9]，实现了3种模型，得到3种模型训练和检验的结果分别如表1和表2所示。

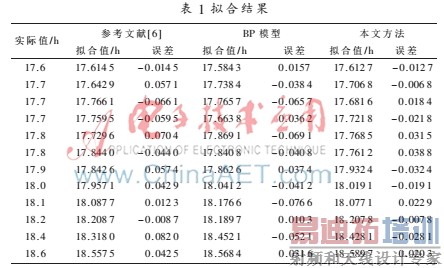
　　以均方误差(MSE)为指标，进一步考察对比本文方法和参考文献[6]方法及BP神经网络方法的预测精度。

　　其中，N为模型预测检验样本的个数，di为模型的期望输出值，yi为模型的预测值。比较结果见表2。

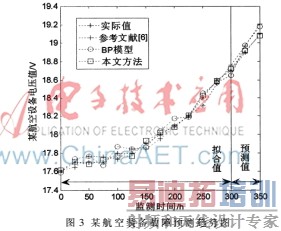
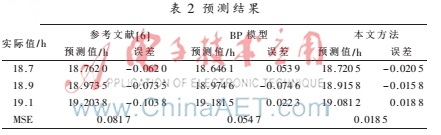
　　综合表1和表2中的数据，可以得到故障预测趋势图，如图3所示。可知：本文方法的预测精度明显优于参考文献[6]方法和BP神经网络方法，而BP神经网络方法比参考文献[6]方法的预测精度略高。这是因为本文方法由于综合了灰色模型和小波神经网络方法的优点，因而具有更好的预测精度，提高了装备故障的预测性能。

　　本文提出一种基于灰色Verhulst-小波神经网络组合模型的装备故障预测方法。该方法综合了灰色Verhulst模型所需样本少、弱化原始数据随机性等优点，以及小波神经网络良好的时频局域化性质和学习能力。以某航空设备为研究对象，建立了其灰色Verhulst-小波神经网络组合预测模型，预测结果表明：本文方法具有良好的预测精度，能够提高装备故障预测的性能，可以为装备维修保障决策提供理论支持。

　　参考文献

　　[1] 王锟，王洁，冯刚，等.复杂装备故障预测与健康管理体系结构研究[J].计算机测量与控制,2012,20(7):1740-1743.

　　[2] 史佩, 高山, 苏艳琴.一种改进的GM(1,1)模型在装备故障预测中应用[J].计算机测量与控制,2012,20(5):1176-

　　1178.

　　[3] 柯宏发，陈永光，胡利民.基于灰色Ver-hulst优化模型的电子装备故障预测方法[J].装甲兵工程学院学报,2012,26(3):65-68.

　　[4] 范爱锋, 孟亚峰, 张宏伟. 神经网络在雷达装备故障趋势预测中的应用[J].火力与指挥控制,2011,36(10):180-181,185.

　　[5] 文莹,肖明清,胡雷刚,等.基于粗糙神经网络的航空电子设备故障预测研究[J].计算机测量与控制,2010,18(4):807-809.

　　[6] 贾宝惠, 雷先铎. 基于组合预测法的航空设备故障预测研究[J].制造业自动化,2012,34(1):93-94,98.

　　[7] 童新安, 魏巍. 灰色Verhulst-BP网络组合模型在预测中的应用研究[J].计算机工程与应用,2011,47(23):245-248.

　　[8] 刘思峰, 谢乃明. 灰色系统理论及其应用[M].北京：科学出版社,2008:1-7, 94-123.

　　[9] 史峰, 王小川，郁磊,等. MATLAB神经网络30个案例分析[M].北京：北京航空航天大学出版社,2010:1-10，208-218.