基于LCD和改进SVM的轴承故障诊断方法

张美玲1，胡  晓2

（1.中国矿业大学 信息与电气工程学院，江苏 徐州221116；2.中国矿业大学 机电工程学院，江苏 徐州221116）

    摘  要： 针对滚动轴承极易损伤，振动信号表现出非线性、非平稳性等特点，提出一种基于局部特征尺度分解(LCD)和改进支持向量机(SVM)的滚动轴承故障诊断算法。首先对采集到的轴承振动信号进行LCD，分解得到一系列内禀尺度分量(ISC)，通过与经验模态分解(EMD)对比研究，证明了LCD方法的优越性；然后计算所有分量的能量熵值，提取出轴承信号的敏感特征集，输入到经过遗传算法(GA)进行参数优选后的SVM识别模型进行轴承状态的诊断识别。实验研究表明，基于LCD和改进SVM的轴承诊断算法能较好地提取出轴承故障特征信息，对4种轴承状态的识别率高达90%，是一种较为有效的轴承故障诊断方法。

    关键词： 滚动轴承；局部特征尺度分解；遗传算法；支持向量机；故障诊断

    中图分类号： TP277

    文献标识码： A

    DOI：10.16157/j.issn.0258-7998.2016.06.022

    中文引用格式： 张美玲，胡晓. 基于LCD和改进SVM的轴承故障诊断方法[J].电子技术应用，2016，42(6)：81-83，86.

    英文引用格式： Zhang Meiling，Hu Xiao. Fault diagnosis method of rolling bearing based on LCD and improved SVM[J].Application of Electronic Technique，2016，42(6)：81-83，86.

0 引言

    滚动轴承作为旋转机械设备中最常使用的零件之一，在实际工况条件下，设备中大约30%的故障都是由于滚动轴承发生故障损伤引起的^[1]。一旦轴承发生故障，一方面会影响机械设备的工作效率，同时也会留下安全隐患，威胁到工作人员的人身安全。因此对滚动轴承进行故障诊断研究，能有效地减少事故发生，同时能够及时排除故障影响，对损坏零件进行更换，这对机械行业的安全高效发展而言具有不可忽略的工程意义。

    局部特征尺度分解(Local Characteristic-scale Decomposition，LCD)是程军圣等^[2]提出的一种新的信号自适应性处理方法，该方法能够有效地将复杂的多分量信号自适应地分解成一组内禀尺度分量(Intrinsic Scale Component，ISC)之和，非常适用于具有非线性、非平稳性等特点的滚动轴承振动信号时频分析^[3]。当轴承发生故障时，信号的能量将发生变化，提取出不同频带各ISC能量熵值，可以此作为判断故障是否发生的指标^[4]。本文结合LCD和SVM算法，从信号携带的能量特征分析，以提取出的ISC能量熵作为输入特征向量，同时利用遗传算法对SVM的参数进行优选，构建最优SVM分类模型，以提高模型识别准确率，通过训练好的SVM对轴承的工作状态进行诊断识别。

1 故障诊断关键技术

1.1 局部特征尺度分解

    局部特征尺度分解能够根据信号本身信息有效地将信号自适应性地分解为一系列ISC之和^[2]。使得信号分解具有一定的连贯性，以便有效地提取出信号特征，同时任意两个ISC之间是相互独立的，必须满足以下两个条件：

    (1)原始信号任意两个相邻极值点正负性不同；

    (2)对于原始信号x(t)的所有极值点(τ_k，X_k)，k=1，2，…，M，M为极值点个数，其中任意相邻两个极大(小)值点(τ_k，X_k)和(τ_k+2，X_k+2)的连线所构成的曲线在横坐标为τ_k+1的纵坐标：

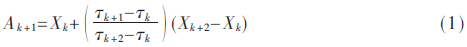
须满足A_k+1/X_k+1的比值近似不变。

    根据以上ISC分量的定义，LCD对信号的分解步骤如下：

    (1)确定原始信号x(t)的所有极值点(τk，X_k)，利用点(τ_k+1，A_k+1)与点(τ_k+1，X_k+1)进行线性插值运算，得到基线信号控制点坐标(τ_k+1，L_k+1)和纵坐标L_k+1=aA_k+1+(1-a)X_k+1，其中a为一常数，通常取0.5。如此，任意两个上述极值点通过以上计算，将原始信号分成了若干个区域，现将任意一个区域进行如下线性变换得到：

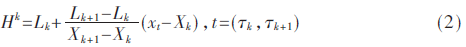
    将所有划分区域变换得到的H^k按区间标号，由小到大首尾依次相连即得到了基线信号H₁(t)。

    (2)将H₁(t)从原始信号中剥离出来，得到新的信号P₁(t)=x(t)-H₁(t)，如果P₁(t)满足ISC的定义，则有第一个内禀尺度分量ISC₁(t)=P₁(t)；如果不满足，则以P₁(t)作为原始信号重复步骤(1)~(2)，直到满足条件为止。

    (3)将ISC₁(t)从原始信号中剥离出来，得到剩余信号r₁(t)=x(t)-ISC₁(t)，继续执行步骤(1)~(2)，得到第二个分量ISC₂(t)。如此往复n次，直到r_n(t)为单调函数或者小于预测阈值，迭代停止，原始信号被分解为：

1.2 基于遗传算法的支持向量机

    支持向量机(Support Vector Machine，SVM)是由VAPNIK等^[5]提出的一种模式识别方法，被广泛应用在机械诊断识别领域^[1]。它的基本思想是将输入样本在另一个与之非线性对应的高维特征空间中构造出其最优分类面。识别模型性能的好坏从根本上依赖于误差惩罚因子C和核函数参数γ的取值情况，这样对支持向量机识别模型的识别率进行优化就转化到对参数取值的优选。

    遗传算法(Genetic Algorithm，GA)是一种仿遗传变异及全局最优点的优选算法^[6-7]。本文将遗传算法应用到SVM参数优选过程，以SVM分类器的分类正确率作为遗传算法个体的适应度。GA-SVM算法具体流程如图1所示。

2 实验装置及数据采集

    测试实验在模拟实验台上进行轴承径向振动数据采集(如图2)，正常轴承和内圈、外圈以及滚动体点蚀故障的振动信号时域图如图3所示。其中，采样频率为5 120 Hz，每种轴承类型振动信号各采集40组，每组信号2 048个数据点。

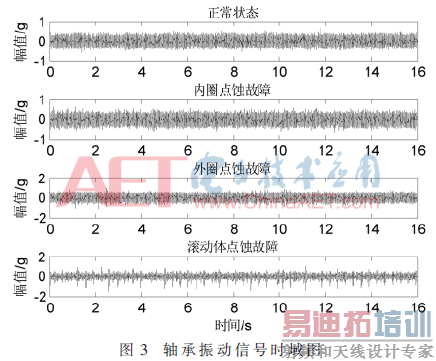
3 轴承振动信号分析

    为了验证本文提出的基于LCD和改进SVM的滚动轴承故障诊断方法的可行性和有效性，首先对采集到的4种轴承振动信号共160组数据进行LCD分解，得到一系列ISC分量。由于篇幅有限，下面以外圈点蚀故障轴承为例进行分析说明。图4为一个外圈点蚀故障轴承信号样本的LCD分解结果，运行时间为0.238 0 s；图5为其经过EMD(Empirical Mode Decomposition)方法得到的分解结果，运行时间为0.475 8 s。对比图4和图5可知，LCD算法相对于EMD算法来说，对信号的分解层次和运行时间都减少，这样有利于减少端点效应在多次迭代过程中对分量的影响，同样也增加了计算效率。对比之下说明了LCD算法的优越性。

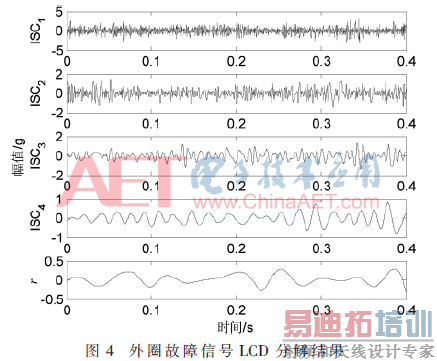
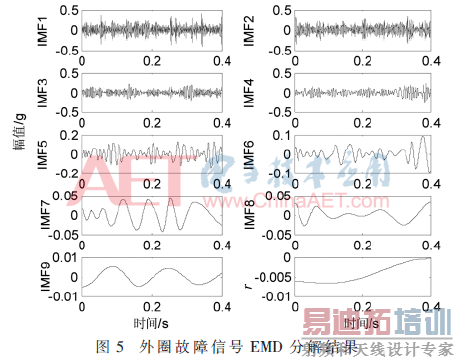
    外圈点蚀故障信号被分解为4个ISC分量和一个余量r，其中主要特征信息被包含在前4个分量中。当轴承发生故障时，振动信号在不同频带所携带的特征信息会发生变化，同时信号的能量分布也会发生变化。下面求取前4个分量的ISC能量熵，并进行归一化处理。各取出3个样本的归一化能量熵分布规律如图6所示。

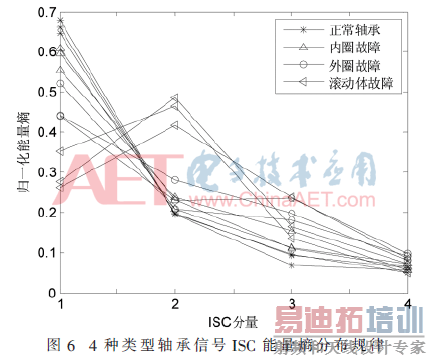
    由图6可以看出，每种类型信号的ISC能量熵分布情况都不太一样，例如滚动体故障能量主要集中在第二个ISC分量，其他3种类型信号能量主要集中在第一个分量；同时能量熵分布有一定程度的聚类现象，可以把这些表现出来的能量熵变化情况作为每种类型信号的特征信息，输入到SVM分类模型中进行诊断识别。每种类型信号各取出30组信号构成训练集，利用遗传算法对SVM的参数C和γ同时进行寻优，最大进化代数为200，种群最大数量20，交叉概率为0.9，变异概率为0.01，交叉验证参数为8。由计算知，最优组合为C=19.289 3，γ=0.374 8，如图7所示。

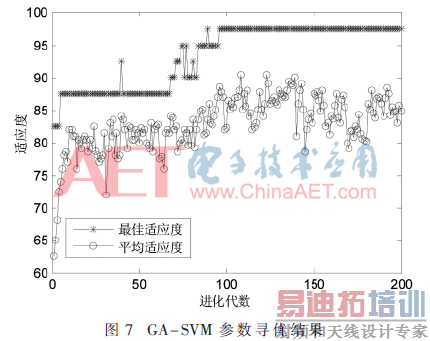
    下面对剩余40组测试集样本进行诊断识别，利用已经训练好的最优SVM识别模型，对于4种不同类型轴承信号的识别结果如图8所示，总体正确率达到90%。其中有两个正常信号被误识别为内圈点蚀故障，两个内圈点蚀故障被误识别为正常信号，原因是在提取故障特征信息时，个别样本的特征比较接近，有重叠现象，所以出现了误识别。

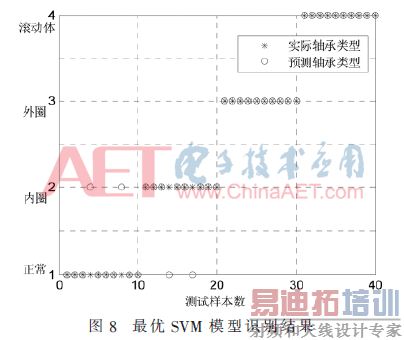
4 结论

    本文采用基于LCD和改进SVM的轴承故障诊断方法，对采集到的振动信号进行自适应性分解，实验过程中还将LCD算法与EMD算法进行对比，从运行时间和分解层次及效率等方面都说明了LCD的优越性；然后提取出ISC能量熵作为敏感特征集，作为SVM分类模型的输入向量，考虑到SVM模型的准确性有待提高，利用遗传算法对SVM的参数进行优选，确定出最佳SVM识别模型；最后利用训练好的识别模型对测试数据进行诊断，对4种类型轴承的识别率高达90%，是一种行之有效的轴承故障诊断算法。

参考文献

[1] 耿永强，危韧勇.基于ICA和SVM的滚动轴承故障诊断方法研究[J].电子技术应用，2007(10)：84-86.

[2] 程军圣，杨怡，杨宇.局部特征尺度分解方法及其在齿轮故障诊断中的应用[J].机械工程学报，2012，48(9)：64-71.

[3] 杨宇，曾鸣，程军圣.局部特征尺度分解方法及其分解能力研究[J].振动工程学报，2012，25(5)：602-609.

[4] 张前图，房立清，赵玉龙，等.基于LCD信息嫡特征和SVM的机械故障诊断[J].机械传动，2015，39(12)：144-148.

[5] CORTES C，VAPNIK V.Support-vector networks[J].Machine learning，1995，20(3)：273-297.

[6] 李兵，张培林，任国全，等.运用EMD和GA-SVM的齿轮故障特征提取与选择[J].振动、测试与诊断，2009，29(4)：445-448.

[7] 都衡，潘宏侠.基于信息墒和GA-SVM的自动机故障诊断[J].机械设计与研究，2013，29(5)：127-130.