集合因子最短路径算法在软件测试中的应用

　　杨会廷
　　(东方地球物理公司 物探技术研究中心，河北 涿州 072750）

       摘要：当前软件普遍采用爬虫程序完成部分测试功能，分析当前测试用的爬虫程序，发现耗时最多的是查找可用路径。为了避免撒网式的、无明确目地的、重复查找，提出了将集合因子最短路径算法应用于当前的爬虫程序中，以改善并提高爬虫程序在软件测试中的效率和有效性。此算法可以大大缩减爬虫程序在查找有效可用路径的时间，提高整个测试的效率。
　　关键词：最短路径；软件测试；集合因子　　

0引言
　　为了满足市场的需要，一般软件都需要支持多个语言版本，例如：微软的Windows 系统和Office软件需要支持几百种语言。因此针对多个语言的本地化软件测试不可避免地提上了日程。在本地化软件测试中，除了本地化的功能测试外，为了保证本地化软件的翻译质量，往往需要对软件的所有本地化页面进行检查。对于支持几百种语言的软件，如何快速有效地获取多种语言的所有本地化页面就成为降低此项测试成本的关键［1］。
1如何获取所有软件页面
　　一个软件有多少界面对于开发者来说是透明的。如何获取一个软件所有的界面，对于不同的软件设计会有不同的策略。基于Web的软件尤为如此。
　　（1）访问URL列表: 这个策略是针对基于Web的软件才可以使用。整个软件所有不同的页面对应的是不同且唯一的URL。通过访问不同的URL以获取软件所有界面是比较简单的方式。前提就是需要获取整个软件的URL 列表。不过目前大多数基于Web 的软件，特别是外网可以访问的软件，为了保证软件的安全都要屏蔽掉实际的URL。所以要获取整个软件的不同URL 列表也不是容易的事。
　　（2）定制脚本：目前许多软件在开发的阶段就同时开始定制许多测试脚本，并在以后的开发测试阶段反复用来测试以保证软件功能正常。但是这些脚本一般都是由开发人员编写的，主要针对软件的功能和复杂的业务逻辑，并且主要运行在英文版的软件上，很少运行在本地化的软件上。根据调查，大概只有6.7%的软件开发小组会把脚本在本地化软件上试运行。所以很多开发脚本都很难直接运行在本地化的软件上并获取本地化的界面［2］。
　　（3）自动爬虫：目前自动爬虫的程序有很多。用户只需要提供登录信息，爬虫程序就能自动查找页面上可能产生的新页面元素，并依次触发，循环迭代直到找到所有页面。为了减少本地化测试成本，对于支持多种语言的软件，要获取多种语言的本地化页面，采取自动爬虫程序是一个很好的选择。让多个线程同时分别运行在多个语言环境下截取所有页面，从而可以大大节省成本。如果让爬虫程序撒网式查找并自由运行，则整个运行过程比较冗长。为了优化爬虫程序，加入最短路径算法，使得整个爬虫程序更有效［3］。
2集合因子最短路径算法的介绍
　　随着社会的发展，最短路径问题在现实生活中占据的地位越来越重要。求解这一类问题的方法有很多，包括Floyd算法、Dijkstra算法、Bellman睩ord算法、动态规划算法和智能优化算法等。最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由节点和路径组成的）中两节点之间的最短路径。算法的具体形式包括［4］：
　　（1）确定起点的最短路径问题：即已知起始节点，求最短路径的问题。
　　（2）确定终点的最短路径问题：与确定起点的问题相反，该问题是已知终结节点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
　　（3）确定起点终点的最短路径问题：即已知起点和终点，求两节点之间的最短路径。
　　（4）全局最短路径问题：求图中所有的最短路径。
　　用于解决最短路径问题的算法被称作“最短路径算法”，有时被简称作“路径算法”。这里主要介绍可以应用于自动爬虫程序的集合因子最短路径算法。
　　2.1集合因子最短路径算法介绍
　　集合因子最短路径算法是单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。其主要特点是以起始点为中心向外层扩展，在扩散过程中每次扩散都以一个集合为因子，直到扩展到所有节点为止。
　　问题描述：在无向图G=(V,E)中，假设每条边E［i］的长度为w［i］，找到由顶点V0到其余各点的最短路径［5］。
　　2.2算法描述
　　2.2.1算法思想原理
　　设G=(V,E)是一个带权无向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每次求得最短路径的顶点, 就被加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
　　2.2.2算法过程描述
　　算法过程如下：
　　（1）初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。
　　（2）从U中选取距离v最小的顶点集合<k1,k2>，把k1、k2加入S中（该选定的距离就是v到k1=v到k2, 且是最短路径长度）。
　　（3）以<k1、k2>组成的集合为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点ki）比原来距离（不经过顶点ki）短，则修改顶点u的距离值，修改后的距离值的顶点ki的距离加上边上的权。
　　（4）重复步骤（2）和（3）直到所有顶点都包含在S中。
　　2.3算法适用范围
　　（1）单源最短路径；
　　（2）有向图和无向图。
3集合因子最短路径算法在爬虫程序中的应用
　　每个软件一般都有一个登录页面，把登录后的第一个页面命名序号为001，然后以从上到下，从左到右的顺序分别定义自动爬虫程序扫描出来的新页面，分别是002、003等。而每个页面之间的距离，即权值，都为1（实际中，访问不同页面需要的时间是不同的，这里在服务器性能很好的情况下，忽略访问时间的不同，都设定为1）。所有页面从第一个页面001出发，可以直接到达或者经过若干个节点后到达。其他不同的节点间也可能存在到达的路径。这样由所有页面作为节点组成一个所有页面可到达的图，且每个节点之间的距离都为1。由于整个软件过于庞大，下面只画出部分节点来说明问题，如图1所示。

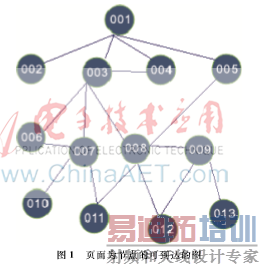
　　设001为源点，求001到其他各顶点〈002，003，004，005，006，007，008，009，010，011，012，013〉的最短路径。算法执行步骤如表1。

4试验数据和性能对比
　　通过对比数据更能体现这一算法应用在爬虫程序中的优势，如表2所示。下面的数据采集采用的是相同性能和型号的服务器，且使用相同软件。整个软件共有956张图。程序运行过程中，在刚开始速度会比较快，到后面时由于需要花费更多时间判断处理，速度会慢下来。表2中的数据属于平均数据。需要运行多个语言平台时，是多个表1算法执行步骤步骤S集合中U集合中1选入 001，此时S=<001>
　　此时最短路径001→001=0
　　以集合<001>为中间点集合开始找U=<002,003,004,005,006,007,008,009,010,011,012,013>
　　001→002=1
　　001→003=1
　　001→004=1
　　001→005=1
　　001→其他U中的节点=∞2选入002、003、004、005，此时S=<001,002,003,004,005>，001→001=0，
　　001→002=1，
　　001→003=1，
　　001→004=1，
　　001→005=1，
　　以集合<002，003，004，005>为中间点集合，从001→002，001→003，001→004，001→005最短路径开始找U=<006,007,008,009,010,011,012,013>
　　002→U中的节点=∞
　　003→006=1
　　003→007=1
　　003→008=1
　　004→U中的结点=∞
　　005→008=1（由于003→008=1已存在，直接放弃此条路径）3选入006、007、008，
　　此时，S=<001,002,003,004,005,006,007,008>，
　　001→001=0，001→002=1，001→003=1，001→004=1，001→005=1，001→003→006=2，001→003→007=2，001→003→008=2，
　　以集合<006，007，008>为中间点集合，从001→003→006=2，001→003→007=2，001→003→008=2
　　分别为最短路径开始找U=<009,010,011,012,013>
　　006→U中的节点=∞
　　007→010=1
　　007→011=1
　　008→009=1
　　008→012=14选入010、011、009，012，此时，S=<001,002,003,004,005,006,007,008,009,010,011,012>，
　　001→001=0，001→002=1，001→003=1，001→004=1，001→005=1，001→003→006=2，001→003→007=2，001→003→008=2，001→003→007→010=3，001→003→007→011=3，001→003→008→009=3，001→003→008→012=3，
　　以集合<009，010，011，012>为中间点集合，从001→003→007→010=3，
　　001→003→007→011=3，
　　001→003→008→009=3，
　　001→003→008→012=3，
　　分别为最短路径开始找U=<013>
　　009→013=1
　　010→U中的节点=∞
　　011→U中的节点=∞
　　012→U中的节点=∞5选入013，此时，S=<001,002,003,004,005,006,007,008,009,010,011,012,013>，001→001=0，
　　001→002=1，001→003=1，001→004=1，001→005=1，001→003→006=2，001→003→007=2，001→003→008=2，001→003→007→010=3，001→003→007→011=3，001→003→008→009=3，001→003→008→012=3，001→003→008→009→013=4U集合已空，查找完毕线程访问同一个服务器，只要改变浏览器的语言即可。从实验数据可以看到在使用集合因子最短路径算法后，不论是单个线程还是多个线程，整个程序的运行时间会大大缩短，性能大幅度提高。
5结论
　　通过把集合因子最短路径算法应用在自动爬虫程序中，使得程序无论在单位时间的吞吐率还是单位事务的响应速度都大大提高。对于某些支持多个语言的软件来说集合因子最短路径算法会使得程序运行效率大幅度提高。
　　参考文献
　　［1］ 张茂林.软件自动测试的研究与程序实现［J］.北京航空航天大学学报, 1997, 23 (1):7480.
　　［2］ 凌永发, 张云生, 郭秀萍. 软件测试自动化的脚本技术 ［J］. 云南民族学院学报(自然科学版)，2002, 11(1):544548.
　　［3］ 王华伟,崔启亮.软件本地化——本地化行业透视与实现指南［M］.北京:电子工业出版社,2005.
　　［4］ 侯俊杰.深入浅出MFC(第2 版)［M］. 武汉:华中科技大学出版社,2005.
　　［5］ 李春葆.数据结构教程［M］.北京：清华大学出版社，2005.