自适应GPS扩展卡尔曼定位算法研究

　　杨  丽，胡方强

　　（南京工业大学 计算机科学与技术学院，江苏 南京211816）

　　摘  要： 针对全球定位系统（GPS）信号定位过程中存在多径导致定位误差，尤其静态环境中零频差短多径引发的定位拖尾现象，提出了一种自适应估计多径残留的扩展卡尔曼滤波算法，实现了静态环境中零频差短多径抑制。首先量化地给出了基带多径抑制后的多径残留模型，即多径呈现“矩形”类型分布，以此为基础设计了一种自适应估计多径残留的方法，即在拟合窗口内估计伪距测量误差的均值和标准差，作为EKF算法的测量误差协方差矩阵，实现了EKF中多径的动态估计。最后通过仿真表明，本文的自适应估计多径残留的扩展卡尔曼滤波（ARKF）能有效抑制零频差短多径影响。

　　关键词： 多径；零频差；扩展卡尔曼滤波；测量误差协方差

0 引言

　　多径干扰是高性能卫星导航接收机的主要误差源，静态环境的多径“固定不变”，导致定位结果在某个方向上形成“拖尾”现象[1]。接收机在静态环境中静止不动，多径与直达信号的多普勒频差为零，静态短多径完全融合在直达信号中，无论从多普勒频率还是从码相位维度都难以鉴别。静态多径会导致伪距测量偏差，虽然定位解算方法可平滑多径影响，但只是简单地将多径近似为随机抖动的高斯噪声，并未考虑多径造成的伪距误差特性[2-4]。因此针对静态场景中常见的零频差短多径提出一种自适应估计多径残留的方法。

1 GPS多径残留模型

　　接收机基带的输入信号为：

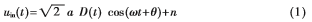
　　复数表达式为：

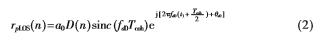
　　假定t1时刻前，只存在直达信号，t1时刻后加入带有多普勒的多径影响，则直达信号多普勒频率fd0=0，多径多普勒频率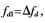多径信号M的复数表达为：

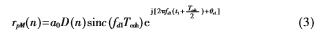
　　在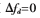时，伪距误差呈现“矩形”分布的特性，在不同多径多普勒情况下，伪距误差呈现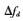周期“震荡”，最高幅度为无多径多普勒频差时的最大误差值[5-7]。因为涉及复杂的变换，伪距误差解析解不易求出，为了简洁地表征多径多普勒情况下伪距变换规律，提出简化模型，用正弦式表示伪距误差：

2 扩展卡尔曼的GPS定位模型

　　扩展卡尔曼滤波基于动态系统模型是高斯分布，其滤波过程主要分两个阶段：预测和更新[8，9]。在预测阶段，滤波器根据上一状态的估计做出对当前状态的估计。在更新阶段，滤波器利用当前状态的观测值去优化在预测阶段获得的预测值， 以获得一个更精确的新的估计值。根据已知的线性观测模型和转移状态模型，可以分别构建出预测过程和更新过程[10]。

　　为实现GPS定位，将扩展卡尔曼滤波算法特殊化，选取状态量为：

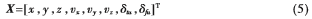
　　同时，选取观测向量为：

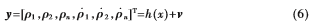
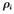　　代表第i颗卫星到接收机的伪距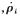为第i颗卫星到接收机的伪距变化率。

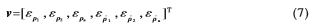
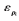　　为该卫星的伪距测量误差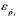，为伪距变化率测量误差。

　　图1展示了GPS定位中EKF的算法流程。

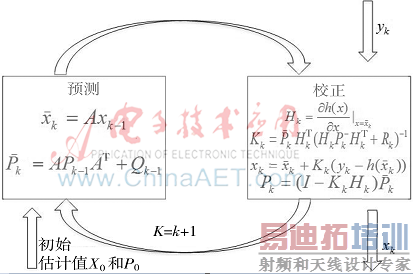
图1  扩展卡尔曼滤波定位解算流程图

　　其中：

　　过程噪声协方差Q为：

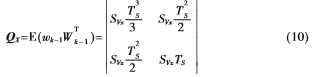
　　其中，SVx为速度噪声（即加速度）功率谱密度值。St为接收机钟差噪声的功率密度，Sf为接收机频漂噪声的功率密度[11-12]。

　　观测噪声R存在多种方法，包括Sage自适应滤波法、卫星仰角权重法、卫星信号载噪比法。本文采用标准EKF功率系数加权的方法设定观测噪声，这是一种计算简单有效的方法[13]。

3 基于多径残留模型的测量误差协方差估计

　　传统的扩展卡尔曼滤波算法只是简单的假设接收机在各观测历元的测量误差服从期望为零的高斯分布，实际上，零频差短多径干扰下的测量误差均值并不为零，这种差异导致定位结果偏离真实状态[14-15]。所以，必须对测量误差期望进行估计，才能得到精确的状态值。根据零频差短多径误差在一段时间内呈“矩形”分布的特点，对测量残差进行开窗拟合，在拟合窗口内对测量残差求平均确定测量误差期望。根据测量误差期望确定当前测量误差协方差，作为自适应参数提供给扩展卡尔曼滤波模型，从而减弱测量误差中多径误差对定位结果的影响。

　　令测量误差向量为vk，测量误差协方差矩阵为Rk，测量误差向量的偏差为uk，因此观测模型的期望不一定为零。

　　当E(vk)≠0时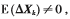，这表明，当一段时间yk存在持续偏差时，E(Xk)≠Xk，即Xk为有偏估计。

　　在有持续偏差时，定位残差向量为：

　　假设在比较短的时间段内，测量误差均值没有发生很大的变化，选取移动窗口长度N，即接收机在tK-N+1到tK时刻共N组观测值，应有：

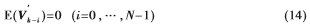
　　将式(13)两端取和再除以N，得到：

　　若不考虑过程转换模型误差，只考虑测量误差对状态估计的影响，则Xk应为无偏估计，即：

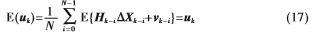
　　表明uk是uk的无偏估计。

　　测量误差协方差与观测残差的关系为：

　　取Rk-i的均值作为Rk的估计值，则有：

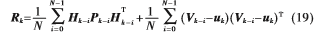
　　可以近似求解tk时刻观测量yk的误差协方差矩阵R，并作为扩展卡尔曼滤波器的自适应参数，实现了基于多径残留模型的自适应扩展卡曼滤波算法。

4 仿真验证

　　通过仿真来验证零频差短多径对EKF、ARKF定位结果的影响。仿真参数为：4颗卫星，GOP为2.5，卫星直达信号载噪比均为40 dBHz，接收机固定，忽略卫星时钟钟差、接收机时钟钟差、大气层延时的影响；其中正南方的一颗卫星在30 s～50 s间引入所示的测量误差，包括伪距测量误差和多普勒测量误差；EKF和ARKF采用了相同的状态方程和过程噪声Q，仅测量误差不同，其中EKF的测量误差协方差采用功率系数加权法，而ARKF的测量误差协方差采用了本文提出的自适应多径残留估计方法。

　　图2给出ARKF中估计的伪距测量误差估计均值与实际值的对比，拟合窗口长度N=5。从图中可以看出：

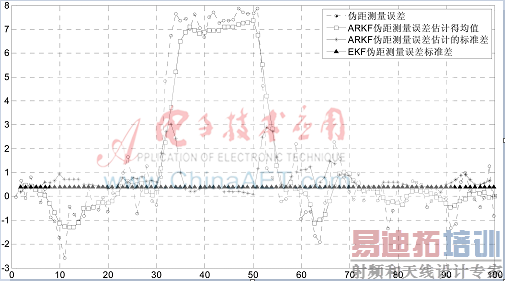
图2  0 Hz多普勒频差伪距测量误差对比

　　(1)EKF中测量误差标准差与卫星C/N0有关，当C/N0为40 dBHz时，其标准差为0.45 m，和无多径情况下的伪距测量标准差基本一致，因此EKF 在无多径干扰时仍然能够较精确地定位。

　　(2)ARKF估计的伪距测量误差均值与实际多径测量误差基本相符，反映了误差变化趋势，当多径引入和多径撤除时，相对误差较大。

　　图3、图4给出了EKF和ARKF的二维定位误差仿真对比图。图3是EKF 2D定位结果图，上述30 s~50 s引入的多径导致了定位点向北偏离了2.2 m。图4是ARKF 2D定位结果图，由于自适应估计了多径，定位点仅仅偏离了0.5 m，多径抑制能力比EKF提升了3.4倍。

图3  EKF 2D定位结果

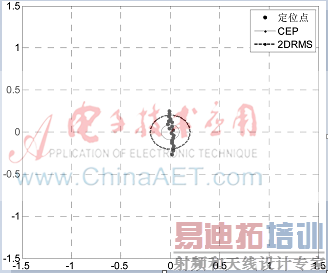
图4  ARKF定位结果

5 结束语

　　为解决GPS定位过程中静态零频差多径带来的困扰，通过量化基带多径抑制后的多径残留模型，即多径呈现“矩形”分布，基于该残留模型提出了测量误差协方差进行开窗拟合的估计方法，以该方法估计的协方差作为自适应参数，用于扩展卡尔曼滤波定位解算，得到更准确的估计接收机的位置、速度等状态，降低多径对定位精度影响。通过仿真表明，本文的自适应估计多径残留的扩展卡尔曼滤波（ARKF）能有效抑制零频差短多径影响，ARKF明显抑制了静态多径造成的“拖尾”效应，定位精度显著高于EKF算法。

　　参考文献

　　[1] BRAASCH M S，VAN DIERENDONCK A J.GPS receiver archi-tectures and measurements[J].Proceedings of the IEEE，1999，87(1)：48-64.

　　[2] RAY J K.Mitigation of GPS code and carrier phase multi-path effects using a multiantenna system[D].Canada：University of Calgary，2000.

　　[3] ASMA R，NICOLAS V，JULIETTE M，et al.Using dirichlet process mixtures for the modeling of GNSS pseudorange errors in urban canyon[C].Proceedings of 22nd International Meeting of the Satellite Division of The Insttute of Naviga-tion(ION GPS 2009)，2009：2391-2399.

　　[4] SAEED D，ALI B.GNSS interference and multipath sup-pression using an antenna array[C].ION GNSS 21st.Portland，OR，2011：1507-1541.

　　[5] MEINHOLD R J，SINGPURWALLA N D.Understanding thekalman filter[J].The American Statistician，1983，37(2)：123-127.

　　[6] 杨长林，柏秀亮.新息自适应区间Kalman滤波算法及其应用[J].传感器与微系统，2012，31(11)：132-135.

　　[7] BISHOP G，WELCH G.An introduction to the kalman filter[C].Proceding of SIGGRAPH，2001，8：41.

　　[8] YAMAGUCHI S，TANAKA T.GPS standard positioning using Kalman filter[C].In：SICE-ICASE，2006.International Joint Conference.IEEE，2006：1351-1354.

　　[9] YU W.Selected GPS receiver enhancements for weak signal acquisition and tracking[D].Canada：Calgary，2007.

　　[10] 鲁平，赵龙，陈哲.改进的Sage-Husa自适应滤波及其应用[J].系统仿真学报，2007，19(15)；3503-3505.

　　[11] 张迎春，李璟璟，吴丽娜，等.模糊自适应无迹卡尔曼滤波方法用于天文导航[J].哈尔滨工业大学学报，2012(1).

　　[12] 田甜，王爱华，安建平，等.一种基于新息自适应卡尔曼滤波的载波跟踪环路[J].第二届中国卫星导航学术年会电子文集，2011.

　　[13] 谢钢.GPS原理与接收机设计[M].北京：电子工业出版社，2009：127-153.

　　[14] 刘基余.GPS卫星导航定位原理与方法[M].北京：科学出版社，2003.

　　[15] 刘亚欢，田宇，李国通.基于最大似然估计的GPS 多径估计[J].宇航学报，2009，30(4)：1466-1471.