- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
七轴机械手最小能量直线轨迹算法优化
摘 要: 对比分析了伪逆法和最优能量算法的原理,给出了最优能量算法的优化方案。笛卡尔空间体系中采用齐次矩阵和四元数法获得位置和姿态的插值;利用优化后的最优能量算法求出逆解,得到与笛卡尔空间中对应的在关节空间中的关节值。文中给出了实际仿真实例,该实例表明本文给出的优化方案在满足正常作业情况下,相对于伪逆法,方案中四元数算法在姿态插值运算上更快并且能量优化效果更好,七轴机械手最小能量消耗节约10%~20%左右。
关键词: 七轴机械手;能量;四元数
0 引言
近年来,冗余度机械手末端执行器广泛应用于装配、喷涂、微操作等工业生产领域。其主要沿直线轨迹进行作业,研究机械臂直线轨迹能量消耗对其实际应用至关重要。目前在冗余机械手优化方面取得了许多有价值的研究成果,主要集中在逆运动学优化和直线轨迹规划两大方面。参考文献[1]给出了一个雅可比矩阵的建立实例及其奇异性分析;参考文献[2]对逆运动学进行了实例分析;参考文献[3]和参考文献[4]提出了冗余机械手的逆运动优化的基于拓展的雅可比矩阵的算法;参考文献[5]中提出了一个求解等式最优化的不使用罚函数或滤子技术的信赖逐步二次规划方法及其全局收敛理论;参考文献[6]中Liu和Yuan等人优化了该理论,并提出了在线搜索逐步二次规划方法及其全局和局部收敛性理论。
在直线轨迹的规划方面,参考文献[7-9]提出了利用Hermite插值和条样、曲线插值等方法来进行直线轨迹规划;参考文献[10]和参考文献[11]则将四元数法引入到机械手轨迹规划的姿态规划中。但其优化效果均不理想。本文对逐步二次规划方法与四元数方法进一步优化对七轴机械臂的直线轨迹进行研究。通过仿真实例表明,相对于伪逆法,方案中四元数算法在姿态插值运算上速度更快并且能量优化效果更好,七轴机械手最小能量消耗节约10%~20%左右。
1 逆运动学的优化
1.1 雅可比矩阵
逆运动学的优化主要利用关联机械臂末端的速度和关节速度的雅可比矩阵J为主要的研究工具来进行,其在机械手运动学中具有重要的作用。令七轴机械手的正运动学方程为:
x=x(q)(1)
式(1)表示操作空间x和关节空间q之间的函数关系,通常用D-H方法来表示。同时对式(1)两边对时间t求导,即可得出笛卡尔空间的速度x与关节空间的关节速度q之间的关系:

对于七轴机械手来说,x∈R6×1,J∈R6×7,q∈R7×1。其中,J是关联笛卡尔空间速度与关节空间速度的雅可比矩阵。显然,式(2)中关节速度的反解并不是唯一的。
1.2 伪逆法求雅可比反解
在实际情况下,式(2)一般是相容的,即:rank(J|x)=rank(J),于是式(2)中的关节速度的通解由雅可比矩阵的伪逆和一组任意的7维向量给出:

其极小范数解即令‖q‖2最小的解为:

其中J+∈R7×6称为J的伪逆也称为加号逆,E∈R7×7,Z是任意7维向量,其中‖·‖2为Euclid范数,在实际用伪逆法求解逆运动解时,常选取qs为式(2)的反解。
当机械手臂处于非奇异位置时,此时J为行满秩矩阵J+=JT(JJT)-1;当机械手处在奇异位置时,rank(J)<6,此时可用最大秩分解法将J分解为Q、R两个行满秩或列满秩矩阵再分别求Q和R的伪逆。这时,J的伪逆可表示为J+=Q+R+,但是在实际运用中上述两种算法运算量都比较大,一种时间复杂度更小、应用更为广泛的算法是对J作奇异值分解,则:

实际上,为了获得唯一解常选取qls作为唯一的反解,即有q=qls=VD+UTx,尽管得到了逆运动学的解,但在以某些运动学或动力学指标来衡量时,伪逆法并不是最优的。
1.3 在某些指标下的最优雅可比反解
解雅可比矩阵的反解其最终目的是通过反解来使机械手末端在笛卡尔空间内沿着指定的轨迹移动,由式(1)可知:

在实际的数值算法中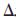 x和
x和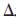 q都代表一定的数值,
q都代表一定的数值,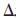 t是其运行时间,则对其优化问题可以转化为线性方程组下的最值问题。
t是其运行时间,则对其优化问题可以转化为线性方程组下的最值问题。
现设xs和xn分别为开始时刻ts和当前时刻tn的机械臂末端6个自由度的值,qs和qn分别为开始时刻ts和当前时刻tn的7个关节空间角度值。并在此时有式(1)成立,则此时可以根据式(7)来进行优化。
一般情形下,优化指标函数为关节角度的二次项形式为:(qn-qs)TH(qn-qs)+c(qn-qs),其中H是正定或半正定矩阵,一般为diag(h1,h2,h3,…,h7),为7×7阶的对角阵,c∈R1×7。在一条轨迹确定的情况下,式(7)中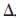 x是已知的,则式(7)是含有6个方程、7个未知数的线性方程组。因为在tn时的优化指标函数是最优的,那么经过
x是已知的,则式(7)是含有6个方程、7个未知数的线性方程组。因为在tn时的优化指标函数是最优的,那么经过 t时刻时的优化目标函数是:
t时刻时的优化目标函数是:
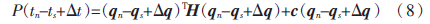
由于qn-qs在tn+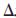 t时刻是已知的,所以对P(q)的常数部分不予考虑,因此P(q)与下面的优化函数Ps(
t时刻是已知的,所以对P(q)的常数部分不予考虑,因此P(q)与下面的优化函数Ps( q)等价:
q)等价:

由于关节空间的角度值qn+
驻q具有一定的限制,qn+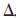 q∈[θmin,θmax],因此有以下限制条件:
q∈[θmin,θmax],因此有以下限制条件:
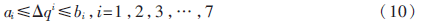
其中ai,bi∈{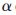 ∈R|0≤
∈R|0≤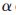 ≤2π},且ai≤bi。
≤2π},且ai≤bi。
现在的目标就是在式(7)和式(10)成立的条件下求出式(9)的最小值。由参考文献[6]可知其充分必要条件(即Kuhn-Tucker条件)为:
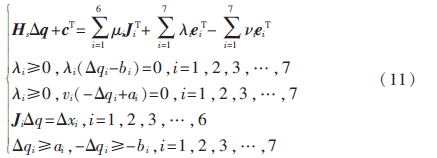
这就把问题转化为一组线性不等方程组,其中i,λi,νi都为未知数,此时要做的就是解出这个方程的一组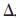 q求出最优解。参考文献[6]中所提出的解线性不等式组的旋转算法可以很好地求解式(11)。
q求出最优解。参考文献[6]中所提出的解线性不等式组的旋转算法可以很好地求解式(11)。
1.4 逆运动解
上面利用雅可比矩阵为研究对象提出了两种求解逆运动学反解的算法,但是实际应用中,利用求其积分来得到运动学的逆解是有一定误差的。在实际的逆运动学中是通过反馈法来实现其运动学校正的。由期望的任务空间的轨迹路径xd和实际的任务空间的轨迹路径xr偏差来不断迭代纠正,直到最后的解在误差范围内。
2 直线轨迹规划
2.1 模型的描述
机械臂在完成作业时,夹手的位姿可用一系列Pi点来描述,所以进行直线轨迹规划的首要问题是解决直线中相邻的两个点的轨迹规划问题。设Ps为直线轨迹的路径起点,Pd为直线轨迹的路径终点,U为全局坐标系,R为机器手底座坐标系。一般从起点Ps到达终点Pd的运动可表示为从
RPs=RTuUPs(12)
到
RPd=RTuUPd(13)
则从Ps到Pd的运动可表示为:
RPd=RTsD(14)
综合式(12)~式(14)得:
D=RPS-1RPd=UPS-1UPd(15)
其中,D包含从Ps到Pd的距离和角度等信息,可表示为:

其中,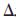 n,
n,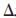 o,
o,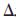 a表示机械手的姿态向量,
a表示机械手的姿态向量,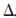 p表示机械手的位置向量,即从Ps到Pd时转过的角度或经过的空间距离。在进行规划时,主要对这些参量进行插值,而产生一系列的运动轨迹数据。
p表示机械手的位置向量,即从Ps到Pd时转过的角度或经过的空间距离。在进行规划时,主要对这些参量进行插值,而产生一系列的运动轨迹数据。
2.2 直线轨迹位置规划
从Ps到Pd所经过的空间距离可用式(16)中的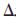 p表示,其中Ps和Pd在机械手坐标系的位置参数为ps={xs,ys,zs},pd={xd,yd,zd}。如果采用S型加速曲线,确定实现轨迹的总时间为ta,插补中每两点之间的插补周期为T,那么总的插值点数为Np=ta/T」+1,并设插值函数Il(n),其定义根据不同的情形而定,一般可取n/Np,其中,n∈{x∈N*|0≤x≤Np},Il(n)∈[0,1]。于是得出插值点在机械手坐标系的位置坐标为:
p表示,其中Ps和Pd在机械手坐标系的位置参数为ps={xs,ys,zs},pd={xd,yd,zd}。如果采用S型加速曲线,确定实现轨迹的总时间为ta,插补中每两点之间的插补周期为T,那么总的插值点数为Np=ta/T」+1,并设插值函数Il(n),其定义根据不同的情形而定,一般可取n/Np,其中,n∈{x∈N*|0≤x≤Np},Il(n)∈[0,1]。于是得出插值点在机械手坐标系的位置坐标为:

2.3 直线轨迹位姿规划
2.3.1 姿态矩阵与四元数
从Ps到Pd的姿态变换可用式(16)中的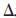 n,
n,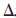 o,
o,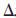 a表示为:
a表示为:

从Ps到Pd的轨迹不仅包含位置的变换还伴随着姿态的变换,可以看出机械手的末端沿着 驻p向量所指示的方向移动的同时进行姿态的旋转,式中 驻n, 驻o, 驻a包含了旋转中的角度信息,可以从式(18)解析出。建立围绕 驻p的旋转矩阵,然后再根据获得的角度信息进行旋转角度插值,最后获得插值中间点的姿态矩阵。但是,这种方法每次插值需要进行大量的矩阵运算,速度比较慢,可用四元数法对姿态矩阵和旋转进行解析,然后再进行插值。下面将论述这种方法的原理。
由参考文献[10]可知四元数的定义为:
q=[w,v]=[w,(x,y,z)](19)
其中v∈R3×1,如果q为单位四元数,则相应的姿态变换矩阵为:

由式(19)和式(20)得到四元数与姿态矩阵的关系,可以看出四元数不仅节省空间而且具有更高的运算效率。
2.3.2 姿态轨迹规划
机械手末端的执行机构的位姿为pc,那么机械手末端执行机构绕向量r转θ角度之后的机械手执行机构的位姿为:

pr=Rpc(22)
因为式(18)中的Tpos表示从开始位姿Ps旋转到位姿Pd的位姿变换矩阵,可以求出Tpos对应的四元数ppos,将其表示为R的形式,由于已知围绕旋转的向量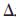 p即R中的r,那么就可以求出从Ps到Pd旋转的角度值。
p即R中的r,那么就可以求出从Ps到Pd旋转的角度值。
求出从Ps到Pd旋转的角度值 茁后,又由于对姿态旋转的插值就是对旋转量的插值,定义姿态插值函数Ip(n),结合2.2节中Np表达式,其中,n∈{x∈N*|0≤x≤Np},Ip(n)∈[0,1]。则可得位姿插值四元数:
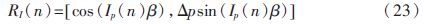
中间每一个插值点的位姿可表示为:
pp(n)=RI(n)pc(24)
当n=Np时,上式与式(22)等价,借助于式(19)与式(20),可获得每一个插值姿态四元数对应的姿态矩阵:
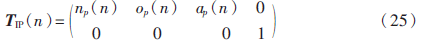
上式为其姿态插值矩阵,联合式(17)可得在每一个插值点处的位姿坐标参数为:
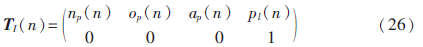
其中,n=1,2,3,……,Np。对于上述插值点之间的插补运动,应根据实际操作的精度和机械手自身的精度来决定采用三次或五次条样连续插补或者更高阶次的插补。这样可以保证机械手直线规划时运动的精度,即运动时偏差比较小。
3 直线最小能量轨迹规划仿真及分析
本文以七轴机械手为研究对象,在三维空间中它具有一个冗余度。本文给出的一般逐步优化函数的形式为P(t)=xTHx+cx,其中x代表机械手的角速度,本文以H=diag(1,2,3,4,5,6,7),c=(1,1,1,1,1,1,1)为例,来求出以上述能量函数为目标函数的最优轨迹规划,其D-H参数表如表1所示[1]。

采用以上参数在MATLAB上进行实验,采用本文第2节所述直线轨迹规划方法获得插值点,之后利用本文1.2节和1.3节所提出的不同的求逆解的方法来求出逆解。利用直线轨迹的起点和终点,并确定机械手的运行周期和轨迹运行总时间,由此确定了直线轨迹上的插值点总数和每一个插值点位姿坐标,从而确定了整条轨迹,图1给出了所规划的直线轨迹。

规划了直线的轨迹之后,利用伪逆法、最小能量法、参考文献[3]和参考文献[4]提出的逆运动学优化方法来对上述逐步优化函数求积分,即可得到能耗函数表达式:

求出上述4种方法的耗能并作比较,图2给出了2.5 s内这4种方法的耗能曲线。

上图中处于最上面的曲线是未优化的能耗曲线,即采用伪逆法来求逆解的能量损耗。处于最下面的是采用能量优化之后的能耗曲线。从图中可以看出,最小能量法比伪逆法要节省能量10%~20%左右,并且比参考文献[3]和参考文献[4]的优化方法更节省能量。
4 结束语
本文介绍了机械手运动学模型中的雅可比矩阵,然后说明了求解逆运动学问题的伪逆法,随后针对伪逆法的耗能过高等问题提出了基于逐步二次项能量最优化的优化算法。对于直线轨迹的规划问题,文章先根据运动模型导出直线轨迹的变换表达式,然后利用四元数法运算高效等优点进行直线轨迹插值,最后将两者综合进行综合仿真。从仿真结果来看,本文介绍的方法具有一定的推广价值。
参考文献
[1] 李诚,谢志江,倪卫,等.六自由度装校机器人雅可比矩阵的建立及奇异性分析[J]. 中国机械工程,2012,23(10):1165-1174.
[2] Xu De, CALDERON C A A, GAN J Q, et al. An analy-sis of the inverse kinematics for a 5-DOF manipulator[J]. International Journal of Automation and Computing, 2005,2(2):114-124.
[3] 廖柏林,梁平元,杨喜.基于伪逆的冗余机械臂运动控制的优化方案[J].信息与控制,2013,42(5):646-652.
[4] 阳方平,李洪谊,王越超,等.一种求解冗余机械臂逆运动学的优化方法[J].机器人,2012,34(1):17-22.
[5] GOULD N I M, TOINT PH L. Nonlinear programming without a penalty function or filter[J]. Mathematical Programming, 2010,122(5):155-196.
[6] LIU X W, YUAN U. A sequential quadratic programming method without a penalty function or a filter for nonlinear equality constrained optimization [J]. SIAM Journal on Optimization, 2011,21(2):545-571.
[7] Su Benyue, Zou Liping. Manipulator trajectory planning based on the algebraic-trigonometric hermite blended interpolation spline[J]. Procedia Engineering,2012,29(1):2093-2097.
[8] PETRINEC K, KOVACIC Z. Trajectory planning algori-thm based on the conti-nuity of jerk[C]. Mediterranean Conference on Control and Automation, 2007, Greece Athens:IEEE Press, 2007:1-5.
[9] BRAVO F, CUESTA F. Continuous curvature path generation based on-spline curves for parking manoeuvres[J]. Robot Auton Syst,2008,56(4):360-372.
[10] SMOEMAKE K. Animating rotation with quaternion curves[J].Computer Graphic-s, 1985,19(3):245-254.
[11] OZDEMIR M. The roots of split quaternion[J]. Applied Mathematics Letters, 2009,22(2):258-263.


