- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
基于多因素模糊和灰色关联度综合的 AIS与雷达数据关联
摘 要: 为提高多目标密集环境下AIS与雷达探测目标关联正确率,将多因素模糊判断和灰色关联度进行结合,提出一种新型关联算法。该算法将目标航迹看作四个因素的时间序列。首先利用多因素模糊判断对四个因素的时间序列集合进行初步关联判断,然后对满足初步关联条件的目标进行四个因素的灰色关联度决策,确定最终航迹相关的目标。仿真证明,该算法相较于单独使用多因素模糊判断,有效提高了关联正确率;相较于单独使用灰色关联度算法,有效缩小了关联范围。
关键词: AIS;雷达;多因素模糊判断;灰色关联度;航迹相关
0 引言
现有的AIS与雷达数据关联方法较多,常用的包括模糊聚类方法[1]、双波门法[2]、K近邻域法[3]、神经网络[4]、灰度关联[5]和模糊理论[6]等方法。上述算法均在不同角度存在不同程度的优势,但在目标密集环境下和交叉、机动航迹较多的情形下,仍可能存在较多的错、漏航迹关联。利用参考文献[5]中灰色关联度方法或参考文献[6]中多因素模糊综合方法进行目标密集环境下的航迹关联,性能严重恶化,本文针对上述问题,提出基于多因素模糊判断和灰色关联度相结合的航迹关联算法,进一步提高目标密集环境下的关联正确率。
1 数据关联算法
1.1 多因素模糊判断航迹相关算法
航迹相似是一个模糊的概念,这里用模糊数学中的隶属度函数来表示。本文采用正态隶属函数来进行初步关联计算,其表示的意义为:两条航迹相距越远,欧式距离越大,隶属度函数值越小。隶属度函数如式(1)[6]:
ξ(ηk)=exp(-τk(ηk2/σk2)) (k=1,2,3,4)(1)
式中,ξ(ηk)为模糊因素中第k个因素的隶属度函数;τk,ηk,σk分别为模糊因素中第k个因素的调整度、欧式距离、展度。
其中因素调整度τk是调整正态函数尖锐程度的参数,这里根据各因素重要程度不同分别设定不同数值。欧式距离计算方法如式(2)[7-8]:
ηk(i)=|UAK(i)-URK(i)| (k=1,2,3,4)(2)
式中,ηk(i)为各因素的欧式距离,UAK(i)和URK(i)分别为通过AIS和雷达获得的i时刻的第k个因素的值。
模糊因素的展度与航迹的误差分布有关,故取各因素欧式距离的均方根值作为各个模糊因素的展度,如式(3):
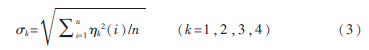
将式(2)和式(3)代入式(1),计算各模糊因素的隶属度函数值。然后利用加权平均计算综合相似度,如式(4)[6]:
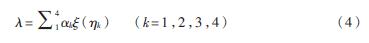
最后进行航迹相关检验。即确定阈值ε(通常取ε≥0.5),比较计算所得综合相似度λ与阈值ε的大小,如果λ≥ε,则判定为航迹相关;否则判定为航迹不相关。
1.2 灰色关联度算法
灰色关联度的关联算法即对于某一雷达目标,计算水域内的AIS目标与其灰色关联度,当AIS目标与雷达目标的灰色关联度大于灰色关联门限时,认为AIS与雷达目标满足关联条件。灰色关联门限在系统的参数设置中可以进行调整。
设雷达探测的目标行为序列为Xi=(xi(1),xi(2)…xi(n)),AIS探测的目标行为序列为Yj=(yj(1),yj(2)…yj(n)),则AIS与雷达目标灰色关联度如式(5)[5]:
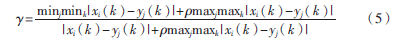
其中,ρ为分辨系数,取值范围为(0,1]。
2 基于多因素模糊判断和灰色关联度的数据关联
由于在一定时间段内,特定船舶的信息只可能与其自身及周围小范围内的船舶信息在位置上存在相关性,所以没有必要对整个水域内的船舶信息进行处理。为了减少计算量,提高计算效率及算法质量,本文提出了基于多因素模糊判断的初步关联判断,经过初步关联判断可以缩小航迹关联的范围,但仍存在误关联,故需利用灰色关联度算法进行二次关联判决以确定最终航迹相关的目标。
本文航迹相关计算步骤如下:
(1)建立模糊因素集。影响航迹相关的船舶的动态信息包括船舶的位置、航向、航速、加速度、转向角等[9],根据互不相关的原则,以上因素可归为四个主要因素,即船舶位置(船舶相对本船距离及方位)、航速和航向。故建立四因素模糊集ν(η1,η2,η3,η4),其中η1表示距离,η2表示方位,η3表示航速,η4表示航向。
(2)确定模糊因素集的权重。上述4个模糊因素中,船位起主导作用,航速次之,航向最小。本文在航迹噪声为高斯随机白噪声的条件下,对几组不同模糊因素权重值分别进行多次仿真分析,得到的关联正确率差别并不大,并未发现某一组值更优,故采用的4个模糊因素集的权重值合理即可,本文采用的分别是α1=0.50,α2= 0.25,α3=0.15,α4=0.1。
(3)确定因素调整度。本文根据各因素重要程度及多次仿真,确定因素调整度分别为τ1=0.01,τ2=0.5,τ3=0.5,τ4=0.5。
(4)根据式(1)计算隶属度函数值,并进行初步航迹相关检验。
(5)对于满足初步关联条件的目标进行灰色关联度判决。
3 仿真分析
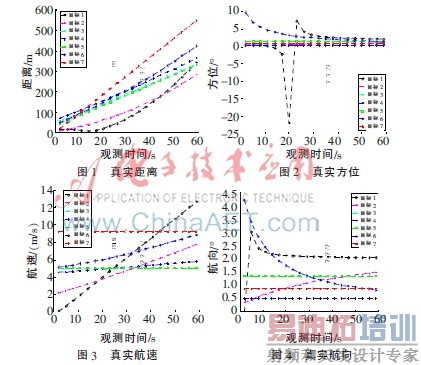
为了验证关联算法的正确性,仿真生成7个密集目标位置数据,如图1~4所示。AIS和雷达噪声均为高斯白噪声。AIS的距离、方位、航速、航向误差分别为10、 0.1、0.4和0.1。雷达的距离、方位、航速、航向误差分别为30、0.4、0.8和0.3。关联时长为1 min。
对各AIS与雷达目标运用多因素模糊进行初步关联判断,设定关联门限为0.7,并对各时刻关联隶属度进行统计,当满足关联条件的时刻点大于等于16个时,认为AIS目标与雷达目标满足初步关联条件。
对满足初步关联条件的AIS目标与雷达目标进行灰色关联度判决,式(5)中的分辨系数经多次仿真验证,当取值小于0.5时,关联错误率达50%以上,当取值介于0.5和1之间时,关联正确率大致不变,均为95%以上,本文取值0.6。得到各因素的灰色关联度值,并进行求和平均,得出各AIS与雷达目标的平均灰色关联度值,在此设定关联门限为0.8。得到结果为雷达7个目标与AIS的7个目标的对应关联。
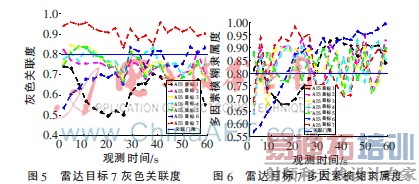
在此以雷达目标7为例给出其与7个AIS目标的关联结果,如图5~6。图5为利用多因素模糊-灰色关联度结合方法所得结果,图6为利用多因素模糊方法所得结果。由图5可见,与雷达目标7相关联的为AIS目标7。而由图6可见,与雷达目标7关联的为AIS目标3(大于关联门限的点数多于16个),关联错误。
在同等仿真条件下,分别利用多因素模糊判断和本文提出的多因素-灰色关联结合方法各进行1 000次仿真试验,得出7个目标的综合关联正确率,如图7所示。
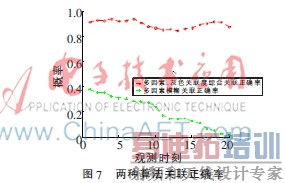
由此可见,本文提出算法与单独使用多因素模糊判断进行航迹相关相比较,明显提高了关联正确率。而且与单独使用灰色关联度方法相比较,缩小了关联范围。
4 结论
本文提出的多因素模糊判断和灰色关联度相结合的方法,可对多目标密集环境下的目标进行正确关联,且关联正确率相较于单独使用多因素模糊判断有显著提高,关联范围相较于单独使用灰色关联度有所减小。
参考文献
[1] 索继东,柳晓鸣,刘人杰,等.AIS的信息融合与雷达目标跟踪[C].中国航海学会2001年度学术交流会,2001:133-136.
[2] 林长川.雷达与AIS目标位置信息融合方法的研究[J].中国航海,2002(1):22-25.
[3] 王国宏,何友.基于模糊综合和统计假设检验的雷达与ESM相关方法[J].系统工程与电子技术,1997(4):13-16.
[4] 胡晓瑞.基于BP神经网络的雷达与AIS目标信息融合处理研究[D].厦门:集美大学,2012.
[5] 郑庆利,田道坤,吴海江.基于灰色关联度的多传感器数据融合方法研究[J].硅谷,2013(1):87-88,135.
[6] 王红杰.基于多因素模糊综合的雷达和AIS情报航迹融合算法[J].信息系统工程,2012(7):136-137.
[7] 关劲.基于模糊理论的雷达/AIS目标数据融合方法[J].舰船科学技术,2010,32(9):67-71.
[8] 马瑞鑫,杨凯,尚东方.基于船舶自动识别系统和高频地波雷达的船舶轨迹数据融合[J].中国水运(下半月),2014,14(5):65-67,185.
[9] KAZIMIERSKI W, STATECZNY A. Fusion of data from AIS and tracking radar for the needs of ECDIS[C]. Signal Processing Symposium(SPS), 2013:5-7.
上一篇:实验室温湿度测量系统设计
下一篇:直齿圆柱齿轮数字测量仪的设计与研究


