基于小波分析与LSSVM的滑坡变形预测

1　引言

由于引起滑坡的地质条件、形成机制、诱发因素等的复杂性、多样性以及变化的随机性,使滑坡的动态信息极难捕捉,故滑坡变形预测的结果难以达到人们需要的精度。由此回归模型、灰色预测模型、人工神经网络模型等在滑坡变形预测中得到了较广泛的应用[1-5]。支持向量机(support vectormachine,SVM)是Cortes等[2]1995年首先提出的一种机器学习算法,基础是VapNIk创建的统计学习理论,能较好地解决小样本、非线性和高维模式识别等实际问题,并克服了神经网络学习方法中网络结构难以确定、收敛速度慢、局部极小点、过学习与欠学习以及训练时需要大量数据样本等不足。Suykens等人[6-10]在Vapnik统计学习理论的基础上提出一种新型支持向量机方法———最小二乘支持向量机(LSSVM),作为SVM的扩展,将SVM的二次规划问题转换为求解线性方程组的问题。小波分析能充分展示变形时间序列的精细结构,即趋势变化、周期变化和随机变化等,帮助研究发现其演变过程,但未对分解后的序列作进一步的分析。因此,提出基于小波分析和LSSVM的预测方法,是利用小波分解的多尺度特性提取原始序列中的高频信息和低频信息,分别利用LSSVM进行回归预测,建立多层次、多尺度预测模型。

2　预测原理与方法

2. 1　最小二乘支持向量机(LSSVM )

根据结构风险最小化(SRM)原则,最大程度地提高泛化能力,避开传统方法存在的“过拟合”问题,且该算法的局部最优解就是全局最优解。最小二乘支持向量机(LSSVM)由Vapnik经典支持向量机发展而来[10, 11],对于回归问题:设有一待回归的数据集D={(x1,y1),…, (xi,yi),…, (xl,yl)},x∈Rn,y∈R,确定一个基于数据集D的函数f(x)=wTφ(x)+b来逼近未知的回归函数。最小二乘支持向量机构造了下面的最小化目标函数:

因此将求解标准支持向量机的二次规划问题转化为利用最小二乘法解线性方程组的问题。

2. 2　基于小波分析与LSSVM的预测模型

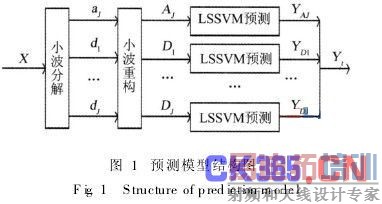
3　工程实例

3.1　实例预测结果为验证上述提出的基于小波分析与LSSVM模型的有效性,以三峡库区兴山县石佛寺滑坡某测点垂直位移观测序列为例。该测点共有80期观测数据,取前60期数据建模,后20期数据用于预测。为了降低建模误差,对滑坡变形数据进行预处理,将数据归一到[-1, 1]区间,得到新的变形时间序列(在建模分析之后,再将其还原到原始区间)。对预处理的变形时间序列{X(t), t=1,2,…,n},选择db8小波进行信号分解。对于小波分解的级数,应根据信号变化的具体情况和数据采样率进行恰当选择。实验研究表明,当信号波动性较强而数据采样点过稀时,过高的小波分解级数会对信号确定性的波动现象进行过滤,引起对原信号恢复的失真,一般情况下,进行4层或5层分解便可达到理想效果。经过实验比较,选择的分解级数为5。原始观测数据及其分解后的各个分量如图2所示。

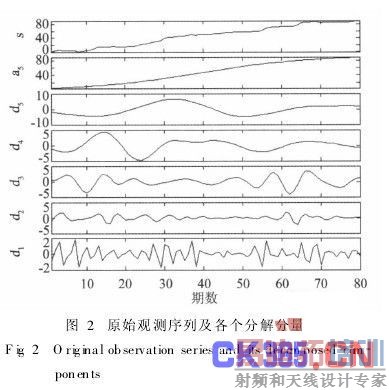
分解后,各个分量序列的数据个数都为80个,选取嵌入维数m,即采用前m个样本的垂直位移序列作为输入量来预报第m+1个样本的观测值,依此类推预报其他期。以低频分量a5为例,表1为对应最小二乘支持向量机模型的输入向量和输出向量。先取前60期数据建模,即把输入向量(x )和输出向量(y )代入式(4),可求得α和b,再由式(5)可预测后20期各分量数据。取嵌入维数m=5,各分量的预测结果如图3所示。

3.2　实验对比分析

分析不同的db小波基和嵌入维数对预测结果的影响,以及与其他方法的对比,可作如下实验分析。在评价预测结果时通常采用以下两项指标:

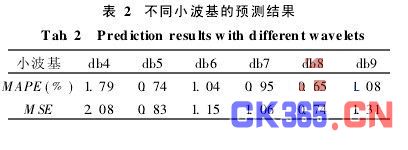
实验1:db小波基的选择。以MAPE和MSE作为评价准则,选取db4, db5,…, db9小波基来进行试验对比分析,此时统一选取嵌入维数m=5,预测结果如表2。

实验2:嵌入维数m的选择。同样以MAPE和MSE作为评价准则,统一选择db8小波基,选取m=5, 6,…, 10进行试验对比,结果见表3。

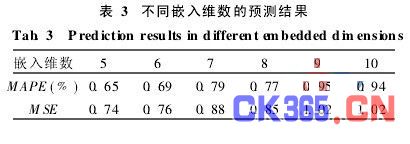
由表2、3可看出,不同的db小波基和嵌入维数对预测结果的影响是不同的,当选取db8小波基、嵌入维数m=5时,预测效果最好。

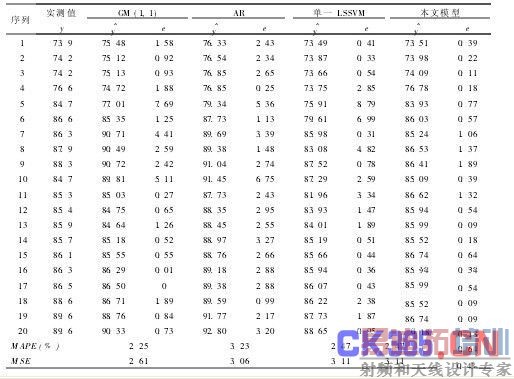
实验3:为了进行对照比较,分别选用GM(1,1)、AR和单一LSSVM模型进行预测,表4为4种模型的预测值和预测残差。

由表4可以看出,基于小波分析和LSSVM模型的预测精度明显高于GM(1, 1)、AR和单一LSSVM模型,表明该模型应用于滑坡变形预测实验中的效果很好。

4　结论

从实测和实验对比,基于小波分析和LSSVM模型的预测精度明显高于GM(1, 1)、AR和单一LSS-VM模型,表明该模型用于滑坡变形预测是可行的,并具有很高的预测精度和较强的泛化能力。