OFDM系统中DAGC的应用研究及FPGA实现

O 引 言

随着各种FFT算法的出现，DFT在现代信号处理中起着越来越重要的作用。在B3G和4G移动通信中所采用的0FDM技术，更是以IDFT/DFT来进行OFDM调制和解调制，IDFT/DFT的精度直接影响基带解调的性能。

在硬件实现中，通常影响定点化FFT算法精度的有量化误差、舍入误差和溢出误差。一旦决定了量化方式和数据位宽后，量化误差和舍入误差都是可估计的，而溢出误差则随着输入信号功率的增大而急剧增加，造成SNR严重恶化。

中射频接收时，通常使用AAGc和DAGC来改善ADC正常工作的动态范围。同理，由于实现高精度定点化FFT算法的难度和成本较高，本文将采用DAGC技术调整DFT输入功率，以降低DFT的实现负担、增加DFT的实现精度、减少DFT的实现位宽。

1 DFT输入功率范围分析

B3G和4G移动通信系统中采用的OFDM技术以OFDM符号为单位进行调制解调，该类系统中高层的子载波分配机制，可以使各个OFDM符号幅度变化较其他通信系统大得多。因此，OFDM符号在接收端中射频进行放大后，传至基带用DFT进行子载波解调，此时的符号功率往往有着较大的动态范围。针对本文关注的DFT溢出误差，该部分将推导DFT所能接收的最大输入信号功率。

复随机序列z[n]=Re(z[n])+jIm(b[n])(n∈[0，N一1])的DFT正变换表示为：

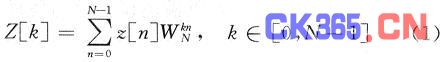
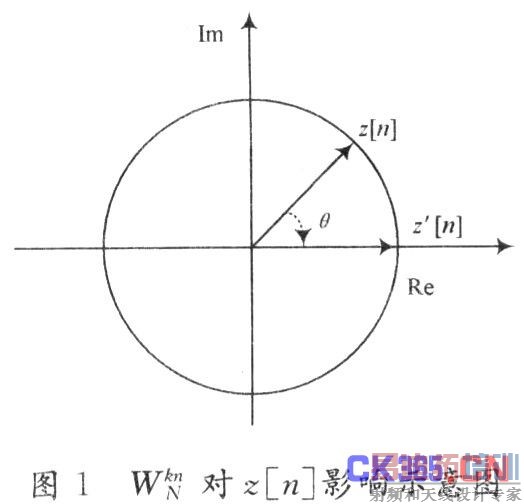
考虑最极端的一个Z[k]，即每一个z[n]乘以旋转因子WknN后，都旋转角θ至Re正半轴成为z’[n]，如图1所示。在这种情况下，定义：

则当虚部为Im(Z[k])=0时，实部Re(Z[k])(k∈[0，(n-1)]的模平方满足：

其中：N为DFT点数，以上推导也可由旋转至Re负半轴，Im正或负半轴得到。因此，所有Z[k]的实部和虚部的模平方必定都小于或等于式(3)所得结果。

本文仅讨论1 024点复随机序列DFT，采用32 b存储DFT结果，高16 b存实部，低16 b存虚部，两个16 b的最高位均为符号位，为了保证DFT后的每一个点都不溢出，则平均功率W，需要满足：

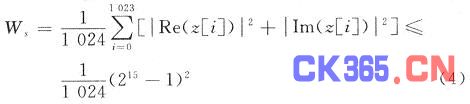
经典的防止DFT溢出的办法，通常是将输入信号的模调整至所允许的最大输出信号模的1/N，N为DFT点数，同样针对以上情况，采用经典模调整方式的平均功率仅为Ws/1 024。

2 数据仿真及分析

针对上面所举例子，用Matlab产生一个长度为1 024的零均值高斯分布复随机序列，序列方差σ2=2k∈[25，215]，k∈[5，15]。定义SNR如式(5)，其中Wfloat，Wfix分别是采用浮点、定点FFT算法的平均输出功率。

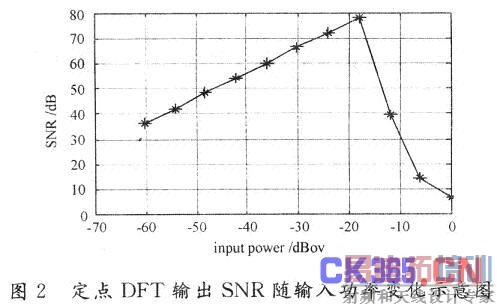
Matlab仿真结果如图2所示，其中横坐标为20logl0(σ2/215)。可见，当输入信号平均功率较小时，量化误差和舍入误差随功率增加而下降，但平均功率上升到一定值后，产生的定点溢出误差增加使得SNR急剧下降。

针对较大的OFDM符号功率动态范围，本文采用DAGC技术来调整DFT输入信号功率，使其处在一个较平稳的范围内，以此提高DFT运算的输出SNR，同时减轻本身就具有较大运算量的DFT模块的负担。根据仿真结果，结合式(4)，选择DFT输入平均功率为(210)2时最佳。

3 FPGA实现及分析

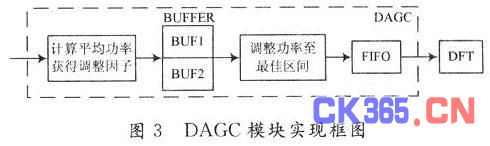
由于用FPGA实现乘除法会消耗大量资源，一般采用左右移位来代替。因此，为了简化FPGA实现难度，本文仅将输入序列的功率从区间[(2i-1)2，(2i)2]调整到[(29)2，(210)2]，其中i为非负整数且i∈[6，15]。

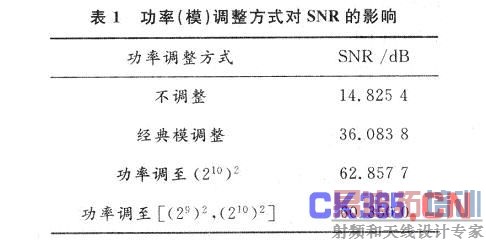
DFT模块选用Altera公司的IPCORE，总体框图如图3所示，其中BUFl，BUF2均可存储1 024点，用于流水处理。该实现方式通过两个二级模块以及中间缓存实现，由于存储功率的寄存器位宽很大，实现时不使用比较器。流水处理1 024点所需要的平均时间la—tency仅为1 029个时钟周期，即经过1 024个时钟周期得到1 024个点后，平均仅需要5个时钟周期得到功率调整因子。本模块综合后的最高频率fmax=220 MHz。以输入序列平均功率为2×(214)2为例，功率调整方式对SNR影响如表1所示，其中第三种方式仅由Matlab仿真得到。可见，采用调整到区间[(29)2，(210)2]时的SNR较高且易于用FPGA实现。

4 结 语

本文主要针对OFDM系统中定点化DFT的溢出误差，分析了DFT输入信号功率对其输出信噪比的影响，并以高斯零均值输入信号为例，采用DAGC与DFT模块级联的方式进行了Matlab仿真和FPGA实现，证明了其可行性。该方法以很小的时延、较少的资源以及较高的精度为优势，有效地增大了定点化DFT正常工作的动态范围，同时为后级恢复原信号提供了可靠保障，完全满足0FDM系统基带解调的要求。