基于灰色模型和 RBF 神经网络的 MEMS 陀螺温度补偿

　　摘要： MEMS 陀螺的零偏随温度呈非线性变化，同时含有较大的随机噪声。针对传统的多项式模型难以精确表达零偏随温度变化的问题，提出了一种基于灰色模型和 RBF 神经网络的 MEMS 陀螺温度补偿方法：首先用灰色模型对数据进行预处理，以减小原始数据的噪声;然后用降噪后的样本数据对 RBF 神经网络进行训练。在相同的训练次数下训练误差可减小一个数量级。验证试验结果表明，采用该模型补偿后的陀螺零偏误差较传统的多项式模型减小一个数量级，较未经预处理的 RBF 神经网络减小 2/3。

　　随着 MEMS 惯性仪表技术的迅猛发展，微机械系统已经得到广泛应用，并取得了一定的军事价值和社会经济效益。基于 MEMS 技术的微机械陀螺仪因具有体积小、重量轻、价格低、寿命长、易集成和适于批量生产等优势，被广泛应用于商业和军事领域。但由于微机械陀螺所采用的硅材料特性以及加工工艺的特殊性，其零位输出随温度漂移的现象非常明显，并且具有复杂的非线性性。常规的温度补偿模型，如 AR 模型、多项式模型[3]，在对 MEMS 陀螺进行建模时难以得到令人满意的补偿效果。灰色系统理论自 20 世纪 80 年代初创立以来，已经在经济、社会、工程和控制等领域得到了广泛应用。灰色累加操作是灰色理论中一个非常重要的特征，它能够减小数据的噪声，使数据变得更加规则。神经网络是由大量简单处理单元所构成的非线性系统，具有联结性、分布效应、并行效应、集体效应和记忆效应等特点，被大量应用在时间序列的建模和预测上。常用的神经网络有反馈神经网络、BP 网络、径向基函数(RBF)神经网络等。文献[8]采用 BP 网络对 MEMS陀螺的温度漂移进行了补偿，达到了较高的精度。然而由于 BP 网络为全局反馈网络，在模型辨识和补偿的过程中需要的计算量很大，往往难以用于陀螺漂移的实时补偿;在模型建立过程中容易陷入局部极小，难以达到全局最优[1]。相比于BP 网络，RBF 网络是一种局部神经网络，无论网络训练还是补偿过程中需要的计算量都小得多。在运用神经网络建模时，其精度往往受到数据随机噪声的影响，噪声越大，网络的训练时间越长，建模精度越低，反之亦然。

　　本文采用灰色模型对 MEMS 陀螺输出数据进行预处理，减小其噪声;然后利用处理后的数据对 RBF 网络进行训练，辨识出温度模型;最后进行高低温试验，比较三种模型下的补偿效果，验证了该模型的精度和有效性。

　　1 灰色理论建模

　　1.1 灰色预测模型

　　灰色模型(Grey Model)是灰色理论中最基本的模型。灰色理论建模过程一般用原始数据列作生成操作，而后建立微分方程并求解。 GM ( m, n )模型中， m 表示微分方程的最高阶数， n 表示变量数。当 n≥ 2时，所建GM 模型不能作预测用。G M (1,1)是灰色模型中应用最为广泛的预测模型，其实质是求解单序列的一阶线性动态微分方程。用 GM (1,1)对陀螺输出进行处理，其具体步骤如下：

　　1)生成累加数列

　　设原始序列为：

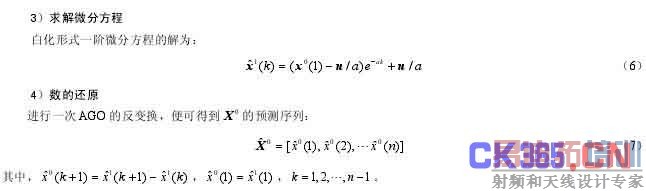
　　在对陀螺输出进行处理时，每增加一个新的信息(陀螺输出值)，便将其加入到0X 中，同时去掉一个最老的信息以保持数列的维数不变，再建立新数列的灰色模型用以预测，这种模型称为等维信息模型。

　　1.2 数据预处理

　　将微机械 IMU 置于静基座下，通电一段时间记录 x 陀螺的输出，如图 1(a)所示。利用 GM (1,1)模型对其进行处理，取步长 n = 50，建立等维信息模型。灰色模型的输出如图 1(b)所示。可以看出，经过该模型处理后陀螺的输出噪声得到了明显的抑制。通常，陀螺零偏的温度补偿是利用陀螺热漂移的历史量测数据建立数学模型，通过模型对零偏进行估计并加以实时修正而实现的。因而，建模所采用的数据的精度与重复性对温度补偿的效果有着很重要的影响。从后文中可以看到，利用灰色模型进行数据预处理，减小数据的噪声，对于模型的精度和最终的温度补偿效果都有显著的提高。

　　2 RBF 神经网络

　　2.1 RBF 神经网络模型

　　径向基函数(Radial Basis Function)神经网络是以函数逼近理论为基础构造的一类前向网络，是一种局部逼近的神经网络，由感觉神经元、联想神经元和反应神经元构成，具有“感觉—联想—反应”结构，如图 2 所示。

　　RBF 网络的基函数的一般形式为：

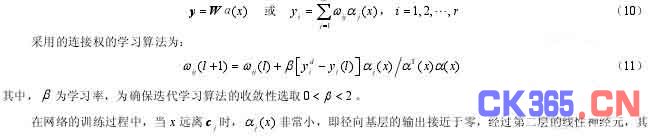
　　输出也接近于零;当 ( )jα x大于某一数值(如 0.05)时才对相应的权值产生影响;当 x 与jc 很接近时，径向基层的输出接近于 1，经过第二层的线性神经元其输出值就更靠近第二层权值。这样训练得到的 RBF 神经网络就具备局部逼近网络学习收敛快的优点。

　　2.2 网络的训练过程

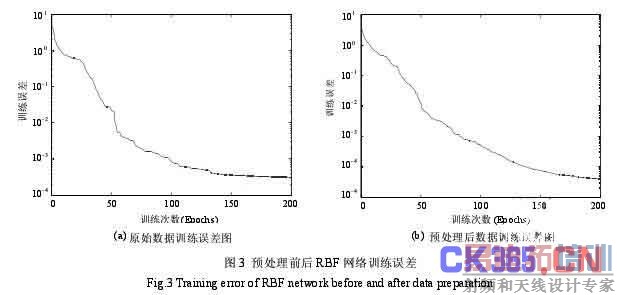
　　利用温箱高低温试验下陀螺的静态输出对网络进行训练。为了比较对陀螺的输出进行预处理前后 RBF 神经网络的特性，分别对预处理前后的陀螺输出数据进行学习，然后比较它们在一定训练周期内所能达到的误差精度。网络的输入量为温度T 、温度变化率d T dt ，网络的输出量为陀螺输出。由网络的映射关系(13)可知，随着数据随机误差的增大，网络的训练时间变长，同时其误差会相应增大。而且，受数据随机误差的影响，网络的精度会随之降低。因此，在对陀螺零偏进行模型辨识前，采用灰色模型对陀螺输出进行预处理以减小数据噪声，对于网络的训练时间和精度都有很大改善。其训练误差比较如图 3 所示。

　　从图 3 中可以看到，当 RBF 网络训练周期同为 200 次时，原始数据的训练误差为 2.167×10-4，而在同样的训练周期，预处理后的数据的训练误差能达到 3.903×10-5，减小了一个数量级。在同样的精度要求的情况下，对数据进行预处理可以节省训练时间，减小神经元的数目，简化网络的复杂度，从而降低实时处理对硬件的要求。

　　3 试验结果与分析

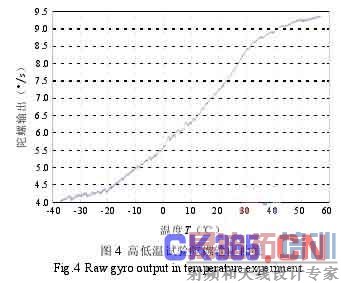
　　将微机械 IMU 置于温箱中，进行-40～60℃的高低温试验， x 陀螺零偏随温度的变化如图 4 所示。分别应用传统的多项式模型[9]、RBF 神经网络以及经由灰色模型预处理的 RBF 网络对 x 陀螺零偏输出进行辨识。然后，利用辨识得到的数据对温度变化下陀螺的零偏进行补偿，补偿后的输出如图 5 所示。三种模型补偿后的误差均值及方差如表 1 所示。

　　从图 5 和表 1 中可以看出，相对于采用传统的多项式模型，用 RBF 神经网络对陀螺零偏进行温补，可以使补偿后的误差均值减小一个数量级;同时，在对陀螺温度模型进行辨识前采用灰色模型进

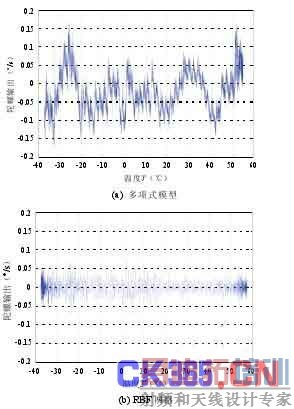
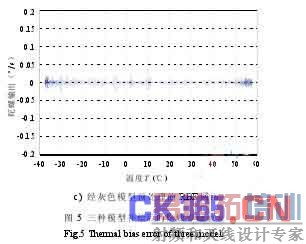
　　行预处理，可以减小数据噪声，提高建模的准确性，并使零偏的误差值进一步减小 2/3 左右。

　　4 结 论

　　针对传统的多项式模型对 MEMS 陀螺建模时误差较大的问题，提出了一种首先利用灰色模型对数据进行预处理，然后利用 RBF 网络进行建模的方法。灰色模型能够减小数据的随机噪声，而 RBF 网络则可以很好地表达陀螺零偏随温度变化的非线性性。利用灰色 RBF 网络、多项式模型以及 RBF 神经网络对高低温试验下陀螺的零偏进行了温补。结果表明，混合模型补偿后的误差较后两种模型分别减小一个数量级和 2/3 左右。但同时，RBF 网络在补偿过程中需要的计算量仍然较大，仍需在基函数的选择及神经元数目上进行优化，以实现工程应用中的 MEMS陀螺实时温度补偿。

　　参考文献(References)：

　　[1] 潘华，李安，胡柏青. BP 混沌混合神经网络在光纤陀螺温度漂移预测中的应用[J]. 中国惯性技术学报，2006，14(6)：73-75.PAN Hua, LI An, HU Bai-qing. Application ofchaos-BP combined artificial neural network inpredicting FOG temperature drift[J]. Journal of ChineseInertial Technology, 2006, 14(6): 73-75.

　　[2] Liu Dachuan, Chi Xiaozhu, Cui Jian, et al. Research ontemperature dependent characteristics and compensationmethods for digital gyroscope[C]// 3rd InternationalConference on Sensing Technology. Tainan, Taiwan,Nov.30-Dec.3, 2008,: 273-277.

　　[3] 张鹏飞，龙兴武. 机抖激光陀螺捷联系统中惯性器件的温度补偿研究[J]. 宇航学报，2006，27(3)：522-526.ZHANG Peng-fei, LONG Xing-wu. Research ontemperature compensation model of inertial sensor inmechaNIcally dithered RLG’s SINS[J]. Journal ofAstronautics, 2006, 27(3): 522-526.

　　[4] 陈殿生，邵志浩，雷旭升，等. 基于递阶遗传 RBF网络的 MEMS 陀螺温度补偿[J]. 中国机械工程，2009，17：2063-2066.CHEN Dian-sheng, SHAO Zhi-hao, LEI Xu-sheng, etal. Temperature compensation for MEMS gyroscopebased on hierarchical genetic algorithm and RBF neuralnetwork[J]. Chinese Journal of Mechanical Engineering,2009, 17: 2063-2066.

　　[5] 伏玉笋，田作华，施颂椒，等. 灰色系统理论、数据预处理及其应用[J]. 上海交通大学学报， 2001，35(2)：268-271.FU Yu-sun, TIAN Zuo-hua, SHI Song-jiao, et al. Grey

system theory, data preparation and their application[J]. Journal of Shanghai Jiaotong University, 2001, 35(2): 268-271.

　　[6] Yu Zhun, Jing You-Yin, Xie Ying-Bai, et al. Applying radial basis function neural network to data fusion for temperaturecompensation[C]//. Proceedings of the Fifth International Conference on Machine Learning and Cybernetics. Dalian, 13-16August 2006: 3177-3180.

　　[7] Huang Guang-Bin, Saratchandrah P J, Sundararajan N. A recursive growing and pruning RBF (GAP-RBF) algorithm forfunction approximations[C]// Proceedings of the 4th International Conferences on Control and Automation, 2003: 491-495.

　　[8] Zhang Qintuo, Tan Zhenfan, Guo Lidong. Compensation of temperature drift of MEMS gyroscope using BP neuralnetwork[C]// International Conference on Information Engineering and Computer Science, 2009: 1-4.

　　[9] Fang Jiancheng, Li Jianli. Integrated model and compensation of thermal errors of silicon microelectromechanical gyroscope[C]// IEEE Transactions on Instrumentation and Measurement Society, Sept. 2009: 2923-2930.