基于白光相移干涉术的微结构几何尺寸表征

　　摘 要: 将 Carré 等步长相移法与白光垂直扫描相结合形成了一种白光等步长相移算法，该方法快速、准确、非接触，垂直分辨力可达亚纳米级. 测量系统集成了 Mirau 显微干涉物镜，并通过高精度压电陶瓷纳米定位器带动物镜进行垂直扫描. 分析了 Carré 法应用于白光干涉信号的相位提取的精度，对不同扫描步距以及不同信噪比情况下的测量进行了计算机仿真，确定了测量参数. 结合重心法将相位计算的数据范围直接定位于干涉信号的零级条纹，从而省去了相位解包裹过程. 通过对微谐振器和标准台阶的测量说明了该方法的有效性，并使用白光相移干涉、白光垂直扫描和单色光相移干涉对 44 nm 标准台阶进行了测量，并对测量结果进行了比较.

　　微纳米技术在过去的 30 年间已经取得了巨大的发展，其各类产品已经越做越小，也就为相应的微结构几何量测量带来了新的挑战[1].进入 20 世纪 90 年代以后，光学显微干涉术，尤其是单色光相移干涉术以其速度快、非接触、场式测量和纳米级分辨力等优势被越来越广泛地应用于微结构形貌检测中. 但是，为了避免测量中的相位模糊，所测量器件上相邻位置的高度差不得大于 1/4 波长，这大大限制了单色光相移干涉术的应用范围. 而白光干涉术与之不同，它使用相干长度很短的白光作为照明光源，有效地克服了相位模糊的问题，很大程度地扩展了测量范围. 目前，如何提高白光干涉的精度和速度，以及如何校正测量中的误差等问题[2]，仍是国际上的研究热点和重点. Roy 等人[3]研究了基于白光干涉膜厚测试中光在膜层内的多次反射带来的影响; Rhee 等人[4]研究了显微干涉术粗糙度测量方法中相移干涉与白光干涉测量结果的差异性，并进行了解释; NIehues 等人[5]将传统的双波长相移干涉技术引入到白光干涉术中，提高了白光干涉的测量精度.

　　正是基于以上背景，本文将 Carré 等步长相移干涉术与白光干涉术相结合，形成了一种具有亚纳米级分辨力并同时具有大范围测量能力的等步长白光相移干涉术，并通过对微谐振器和标准台阶的测量说明了本方法的可行性.

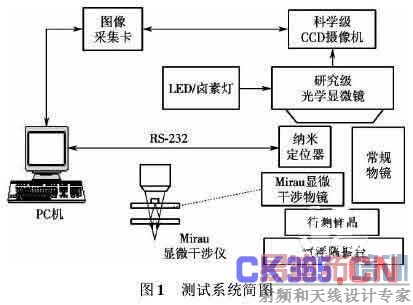
　　1 测试系统

　　本测试系统在 Zeiss Axioplan 2 imaging 型显微镜上集成了 Nikon 公司的 Mirau 型显微干涉物镜. 通过一个高精度压电陶瓷纳米定位器带动物镜完成垂直扫描. 系统使用高质量的白光发光二极管( light emittingdiode，LED) 进行照明. 测量图像通过一个科学级 CCD摄像机进行采集，并通过图像采集卡传输给 PC 机进行后续处理. 整套系统搭建于一个隔振平台上，以减少外界振动对测量的影响. 系统简图见图 1.

　　2 测量原理及仿真

　　2. 1 Carré 等步长相移法

　　Carré 等步长相移法是相移干涉中一种普遍采用的方法. 本文之所以选用此方法的原因之一在于: 对于多数移相器，要求步长相等容易实现，而要精确控制步长为某一具体量值则较难. 假设每一步的移相量为2δ，Carré 相移法可以表示为

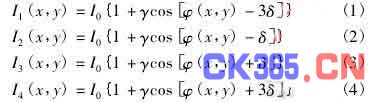
式中: Ii( x，y) ( i =1，2，3，4) 为某一像素处的测量光强值; I0为干涉信号的背景光强值; γ 为干涉信号条纹对比度; φ( x，y) 为待测量的相位，rad( 由于相对于固定的位置，( x，y) 为常数，所以在下文中将把( x，y) 省略) . φ 的测量结果为

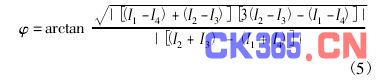
　　此处所得的相位值分布在 之间，将其扩展到( - π，π]后，便可以使用多种解包裹方法得到实际的相位值，如加权最小二乘法等[6]. 表面高度信息与相位的转化关系为

式中: h 为被测表面某一点的相对高度值，nm; φ珔 为 φ解包裹后的相位值，rad; λ 为所用光源的波长，nm. 这样就得到了每一点的相对高度信息，而各点间的相对高度差就反映了表面形貌的真实信息.

　　2. 2 白光相移干涉

　　2. 2. 1 相位计算仿真

　　当使用白光光源代替单色光光源照明进行相移测量时，条纹对比度将不再是一个常数，而受一个高斯函数的调制. 一个典型的白光干涉信号可以表示为

式中: g( z) 为高斯函数; 0为由反射所引入的附加相位，rad. 正是由于 γg( z) 项的出现使 Carré 法应用于白光干涉信号会不可避免地带来误差. 下面本文将对这种误差进行计算机数值仿真. 产生的仿真信号为

式中: Δ 为扫描步距，Δ = 60 nm; σ 为光谱宽度的倒数，σ =500 nm; 附加相位

　　图 2 为模拟信号的相位分布、白光相移法所计算出的相位分布以及相应的误差分布. 从图中可以很明显地看出，测量误差值在白光干涉条纹的零级条纹处为最小值. 而随着位置远离零级条纹，相应的误差值也迅速增大. 其最小误差值小于 0. 02 rad，所带来的测量误差小于当所用白光光源的平均波长为 600nm 时，这个值约为 1 nm，这小于测量中由振动或环境因素等带来的误差. 其原因可以解释为: 在白光干涉信号零级条纹位置附近，其对比度受高斯函数的调制效果弱，所以在此位置附近计算所得的相位值误差最小.实际测量过程中，由于卤素灯或白光 LED 均为宽光谱光源，并且不同的制造工艺过程还会带来不同的光谱分布[7]，这都会影响白光光源中心波长标定的准确度. Carré 等步长相移法对于扫描步长的确定并不依赖于中心波长，所以可以有效地降低由白光中心波长标定带来的误差.

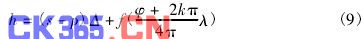
　　2. 2. 2 高度测量仿真

　　从第 2. 2. 1 节中的相位测量模拟可以看出，Carré法应用于白光干涉信号处理是满足测量精度要求的，由此可以得到被测结构的表面高度为

式中: s 为总的扫描步数; p 为相位 φ 所对应的位置;s - p表示扫描方向相对于器件是由上向下进行的; k 为整数; f 为数值孔径参数. k 的存在表明，当相位计算的p 点定位在白光干涉信号的 ± 1 级、± 2 级等非零级的级次上时，需要进行相位解包裹计算，相应对于 ± 1级、±2 级等级次的干涉条纹，k 取值为1，2. 与相移干涉类似，f 的存在表明了干涉物镜的放大倍率对干涉条纹宽度的影响，较大的干涉物镜放大倍率对应着较大的 f 值. 对于这个参数，Creath[8]和 Sheppard 等人[9]都进行过研究，本文也考虑了这种影响并采用 In-gelstam[10]的公式，即

式中 NAeff为有效数值孔径. 以下将基于相位模拟来进行高度计算的仿真，仍以式( 8) 中的模拟信号为例，结果如图 3 所示.

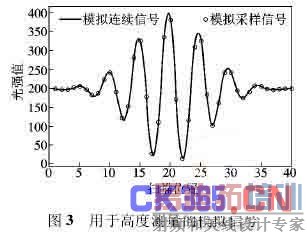
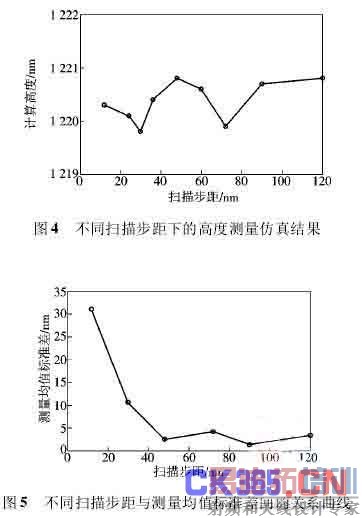
　　图中模拟连续信号的零级条纹约位于 19. 677 处，相应的高度值为1 219. 4 nm. 由前面的相位仿真可知，靠近零级条纹处的相位计算误差最小. 也就是说，当式( 9) 中的 k 取 0 值时，由白光干涉信号调制度变化所带来的相位计算误差最小. 同时，Sandoz 等[11]也出，只有当进行相位计算的数据组定位在白光干涉零级条纹上时，才可以避免后续的相位解包裹过程. 故本文中相位的计算就以图 3 中的第 18、19、20、21 点来进行，所得的高度值为1 220. 6 nm，这也与相位仿真的结果吻合. 在实际测量中，将使用重心法来确定进行相位计算的数据组，从而将相位计算定位在零级条纹上. 图4 表明了不同的扫描步距对高度测量的影响，从图中可以看出，在满足采样定理的前提下，扫描步距对高度测量的影响是比较小的.

　　对理想的白光干涉信号分别加入不同等级的白噪声，使其信噪比为 34 dB、26 dB、20 dB、14 dB 和 12dB; 然后使用一定长度的扫描步距对不同等级信噪比的信号分别进行 6 次测量并取其平均值. 模拟中采用的扫描步距为 12 nm、30 nm、48 nm、72 nm、90 nm 和120 nm. 每种扫描步距与 6 个测量平均值的标准差之间的关系曲线见图 5. 从图中可以看出，当扫描步距为12 nm 时，高斯白噪声对测量结果的影响是很大的，相应的值约为 31 nm. 当扫描步距为 30 nm 以上时，白光相移算法展示出了很好的抵抗高斯白噪声的能力. 综合考虑相位误差与高度测量的仿真，实际测量中本文选用 45 ～70 nm 之间的扫描步距.

　　3 实验结果与分析

　　3. 1 微谐振器的测量

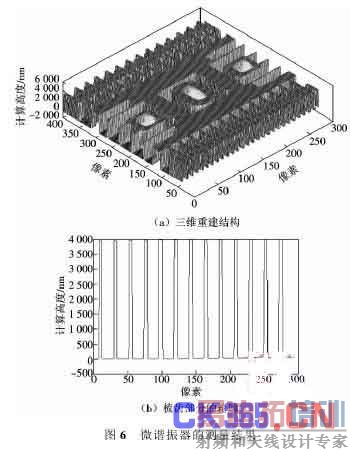
　　本文首先测量了由美国北卡罗莱纳微电子中心( MCNC) 提供的测试用微加工多晶硅水平微谐振器.实验使用 20X Mirau 干涉物镜，采用平均波长为 600nm 的白光 LED 进行连续照明，被测物平放于载物台上. 通过软件控制物镜定位器带动物镜由上自下进行扫描，扫描范围为 9 μm，扫描步距为 45 nm. 测试结果如图6 所示，从图中可以看出梳齿部分的高度约为3. 8μm. 这充分说明了等步长白光相移算法的有效性.

　　3. 2 标准台阶的测量

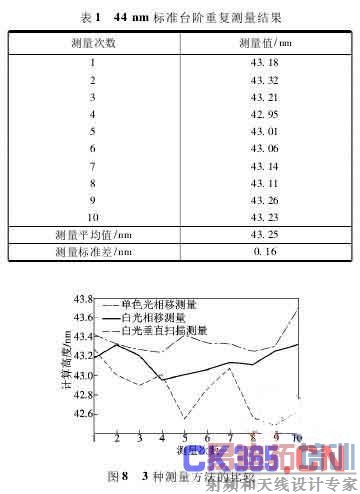
　　采用 Hariharan 五步单色光相移法，白光相移干涉和基于重心法的白光垂直扫描干涉在完全相同的情况下对 44 nm 矩形台阶( 标定值为( 43. 2 ± 0. 6) nm) 分别进行了多次测量. 在单色光相移的测试中，光源的心波长为 625 nm，Hariharan 五步单色光相移法的扫描步长设定为 78 nm; 白光相移干涉和白光垂直扫描干涉的扫描步长均设定为 50 nm. 白光相移干涉测量 44nm 标准台阶的结果见图 7 和表 1. 图 8 比较了 3 种方法的测量结果，等步长白光相移干涉的测量结果位于单色光相移干涉与白光垂直扫描的测量结果之间.

　　4 结 语

　　本文将 Carré 等步长相移法应用到白光干涉术中，形成了一种基于等步长的白光相移干涉算法. 由于本方法采用了等步长而非定步长，所以对于多数移相器而言容易实现，并且由于移相步长的确定不依赖于白光的中心波长，因而减少了通常移相算法中由中心波长标定带来的步长误差. 通过对微谐振器和标准台阶的测量说明了本方法的可行性.

　　参考文献:

　　[1] Guo T，Hu C G，Chen J P，et al. Vertical scanning whitelight interference for dimensional characterization of micro-electromechanical system devices[J]. Acta Optica Sinica，2007，27( 4) : 668-672.

　　[2] Gao F，Leach R K，Petzing J，et al. Surface measurementerrors using commercial scanning white light interferometers[J]. Meas Sci Technol，2008，19( 10) : 015303.

　　[3] Roy M，Cooper I，Moore P，et al. White-light interferencemicroscopy : Effects of multiple reflections within a surfacefilm[J]. Optics Express，2005，13( 1) : 164-170.

　　[4] Rhee H G，Vorburger T V，Lee J W，et al. Discrepanciesbetween roughness measurements obtained with phase-shift-ing and white-light interferometry[J]. Appl Opt，2005，44( 28) : 5919-5927.

　　[5] Niehues J，Lehmann P，Bobey K. Dual-wavelength verticalscanning low-coherence interferometric microscope[J]. ApplOpt，2007，46( 29) : 7141-7148.

　　[6] Marroquin J L，Rivera M. Quadratic regularization function-als for phase unwrapping[J]. Optical Society of America，1995，12( 11) : 2393-2400.

　　[7] Hanhijaervi K，Aaltonen J，Kassamakov I，et al. Effect ofLED spectral shift on vertical resolution in stroboscopic whitelight interferometry[C]/ / Proceedings of SPIE. Strasbourg，France，2008: 70031s-1.

　　[8] Creath K. Calibration of numerical aperture effects in inter-ferometric microscope objectives[J]. Appl Opt，1989，28( 15) : 3333-3338.

　　[9] Sheppard C J R，Larkin K G. Effect of numerical apertureon interference fringe sPACing[J]. Appl Opt，1995，34( 22) : 4731-4734.

　　[10] Ingelstam E. Problems related to the accurate interpretationof microinterferograms[C]/ / National Physical LaboratorySymposium. London，Britain，1960: 141-163.

　　[11] Sandoz P，Devillers R，Plata A. Unambiguous profilometryby fringe-order identification in white-light phase-shifting in-terferometry[J]. Journal of Modern Optics，1997，44 ( 3) :519-534.

　　基金项目: 国家自然科学基金资助项目( 91023022) ; 科技部国际科技合作与交流资助项目( 2008DFA71610) ; 天津市自然科学基金资助项目( 09JCYBJC05300) .

　　作者简介: 马 龙( 1983— ) ，男，博士生，malong9904@ yahoo. com. cn.

　　通讯作者: 郭 彤( 1977— ) ，副教授，guotong@ tju. edu. cn.