薄膜反射镜的成形控制

　　1　引　言

　　作为空间观测的主要手段,采用反射式光学系统的空间望远镜是空间遥感光学系统的主要器件[1]。而传统的反射镜基底材料(如玻璃)面密度大、制作困难[2],难以满足运载设备对光学系统有效载荷、使用空间的限制和对大口径、高分辨率反射镜的使用要求。目前,美国能源部圣地亚国家实验室与肯塔基大学合作,正在研制可展开超轻型大孔径薄膜镜片技术,误差不超过2.5×mm,质量不超过1 kg/,是空间望远镜的未来[3]。所以,空间反射镜的大口径、高分辨率与轻量化是空间技术的主要发展方向之一。

　　随着先进材料技术的发展,被喻为“解决问题的能手”的聚酰亚胺薄膜材料得到广泛应用,其面密度能达到0.05 kg/,且具有良好的物理性能,可应用于空间光学成像、观测系统,能够充分发挥其面密度低、体积小、便携可展、易于控制和成本低的特点,可望解决发射系统承载空间、承载质量的限制与大口径、高分辨率反射镜使用需求之间的矛盾。

　　静电拉伸式薄膜反射镜(EMR)和充气式薄膜反射镜是薄膜反射镜的两种主要成形方式。EMR是通过分布式高压静电电极对镀金属的树脂薄膜进行静电拉伸变形来实现光学成像的,相对充气式薄膜反射镜来说,能够实现精确控制成形[4]。大口径EMR的研究始于上世纪70年代末[5],世界上很多研究单位都已开展了对EMR的研究,包括美国NASA、亚利桑那大学、欧空局、英国苏格兰大学等等。国外相关报道只停留在上世纪80年代,目前则很少,由于技术保密,详细信息很难获得。国内只有长春光机所和苏州大学正在进行薄膜反射镜研究,但尚处于薄膜成形机理摸索阶段[6-7]。长春光机所已率先进行了口径为Φ180 mm的单电极EMR实验和相关理论分析,为Φ300 mm或更大口径多电极EMR的精确成形控制研究奠定了基础。可见,深入开展EMR的研究具有重要意义。

　　2　理论计算

　　EMR面形控制的中心问题是找到使薄膜变形达到理想面形所需的分布电极电压,也就是找到薄膜若干点的薄膜所受横向力与面形变形量之间的关系,以及将薄膜所受横向力转换成电极电压。

　　相对于目前广泛研究的薄膜大变形求解问题来说,薄膜的小变形问题[8]是指薄膜变形的挠度角比较小,薄膜的预应力在横向力的作用下不受薄膜变形影响,而且各向相同。当然,这依赖于膜材的弹性极限、弹性模量和薄膜边界预应力调节。薄膜的小变形问题可通过求解泊松方程来解决[9]。薄膜的小变形可表示成薄膜所受静电拉伸横向力的线性关系,然后再利用最小二乘法拟合成理想面形[8]。为了求解薄膜的变形问题,下面用泊松方程来描述薄膜变形与薄膜所受横向力之间的关系:

　　其中,z为薄膜变形,P为薄膜所受横向力,T为薄膜预张力。为了方便计算将半径归一化,即r/R=1时,z=0。根据文献[8],泊松方程在极坐标(r,)下的近似解析解为:

　　式(3)可写成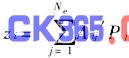,即薄膜的小变形量可表示成与作用电极电压变化的线性关系,其中,为面形的影响函数[8]。系数Aij由泊松方程求解得出,zi是面形上的第i点(极坐标位置为(ri,i))变形量,Pj是第j个电极作用在面形上的压力,Ne是电极数目。

　　其中,

　　式(4)依据ri和第j个电极的径向边界值r1j和r2j分解成五种解析表达式[8]:

　　第一种:ri=0,r1j=0,中心电极对面形中心的影响系数:

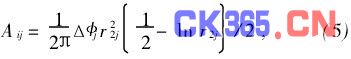
　　第二种:ri=0,r1j>0,非中心电极对面形中心的影响系数:

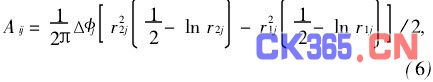
　　第三种:r2j≤ri,电极对外围面形的影响系数:

　　第四种:ri≤r1j,非中心电极对内围面形的影响系数:

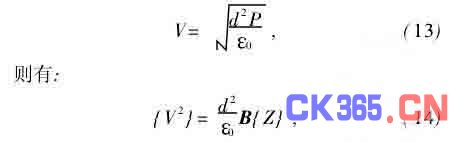
　　第五种: r1j

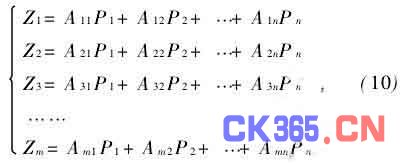
　　以理想面形为目标,则各个电极所施加电压变化量{Pn}可依据最小二乘法求解线性方程组{Zm}=Am×n{Pn}得出,其中面形控制矩阵是由各影响函数离散后线性组成的。

        由于对薄膜反射镜的直接输入参数是电极电压V,而[8]:

        其中,d为所测量点到电极面的距离,ε0为真空介电常数。这样当给定指定点的薄膜变形值时,所施加的电极电压就可求。

        由表1参数,取m=6,n=3,在薄膜径向上按0.025 m步长均布采点,由公式(4)~(9)有:

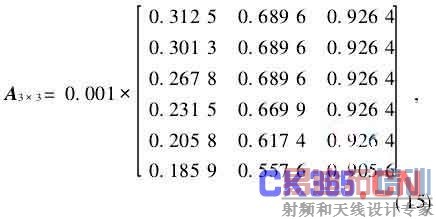
       由式(12)~(16),以一定面形(抛物面、球面等)为目标时,就可计算相应横向载荷和分布电压。因此,控制方法大致可归纳为4步:

        (1)在需要理想成形的薄膜面形上选择适当间距和数量的采样控制点;

　　(2)确定面形取样点上的影响函数矩阵;

　　(3)通过最小二乘法求解分布电极最优作用横向力从而使薄膜理想成形;

　　(4)将所求作用横向力转变为分布电极上所施加的电压。

　　3　验证分析

　　通过有限元仿真验证分析了提出的控制方法。首先,通过施加温差ΔT来模拟外腔对薄膜的预张力调节[6]。根据薄膜热膨胀系数与热应力的关系,薄膜预应力为S=Eαh(ΔT)(N/m)。降温,则薄膜预张力提高。在ANSYS中建立薄膜有限元模型,采用三角形膜单元shell41划分,结点数为300,单元数为566,取ΔT=-0.2℃。针对薄膜中心不同变形量的理想抛物面,将由公式(15)~(16)计算所得横向力值分别施加于图1分布式电极所对应面形,进行对比分析(见图2)。

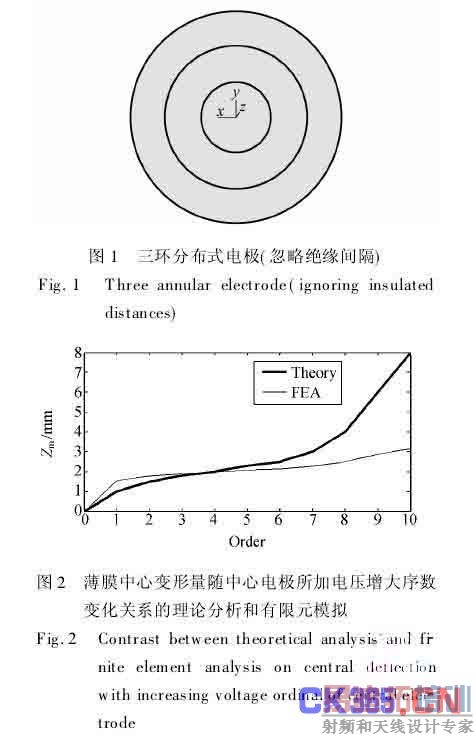
　    由图2可知,随着中心电极所加电压的增大,薄膜中心变形量增大,当变形量<2.5 mm时理论计算变形值和有限元分析变形值接近,变形量在1.946 mm时计算变形值和有限元分析变形值重合。当Zm=1.946 mm时,以理想抛物面为目标,三环分别施加的横向载荷由式(15)、(16)通过最小二乘法计算得1.730 4、4.953 4、2.181 2 N/,相应电极电压为4.421 8、7.481 3、4.964 5 kV,所得面形如图3所示。有限元模拟面形与理想抛物面形在6个采样点的均方根误差rms =0.215 94 mm。由于拉伸过大时理论计算值不满足泊松方程小变形条件,故理论计算变形值和有限元分析变形值大约在2.5 mm以后偏差较大。

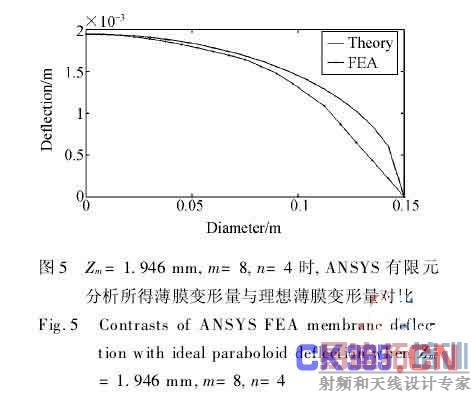
　　通过有限元仿真分析(图4)可知,中心电极对应的薄膜面形控制较好,第二、三环电极对应的薄膜面形控制不理想。可见薄膜表面预应力一定的情况下通过三环分布式电极精确控制面形精度是远远不够的,它的精度依赖于计算面形影响函数的精度,而且也和膜材弹性属性等有关。由于这里只取单一径向上6个采样点,忽略绝缘间隔的条件下针对环电极进行的计算,势必会造成控制矩阵计算、拟合的误差,从而直接影响计算面形与理想面形或实际面形的偏差。沿单一径向将电极均匀划分为n= 4部分,在面形上按步长0.018 75 mm均分采样控制点,即m=8。当Zm=1.946 mm时,同理求得四环分别施加的横向载荷为2.839 0、1.978 1、6.035 1、5.703 1 N/m2,相应电极电压为5.663 8、4.727 7、8.257 9、8.027 6 kV,有限元模拟面形与理想抛物面形在8个采样点的均方根误差rms=0.164 30 mm(图5),明显优于m=6,n=3情况。如果只增加采样控制点数,而保持电极环数不变,则求得的面形均方根误差过大。因此,只有在一定范围内增加薄膜外围区域的采样控制点数量和相应的环电极数量,方可有效提高面形精度。另外,也可以扩展到每一环上周向细分的分布式电极,针对每一个细分电极求影响函数,通过取多点来进行拟合计算,减小面形误差。所取采样控制点应尽量布满整个面形,以获得最佳拟合效果,实现面形控制的准确性。

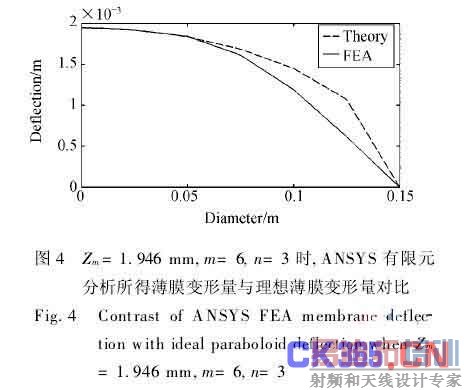
        此外,较高的薄膜表面预应力可有效调节薄膜面形精度[6],但往往会造成过高的电压施加,因此合理选择薄膜表面预应力也是薄膜精确成形控制的关键,这里不详细分析。

        4　结　论

　　通过ANSYS有限元分析软件定量分析了口径Ф300 mm的同心环分布式电极静电拉伸聚酰亚胺镀铝薄膜反射镜基于泊松方程小变形求解的有效范围。当薄膜中心变形量大约<2.5 mm时,基于泊松方程的理论求解和ANSY有限元分析结果基本吻合。当其它条件一定时,增加薄膜外围区域的采样控制点数量和相应的环电极数量,对于提高面形精度是可行的。只有综合运用数值计算、有限元分析和实验的方法,通过确定分布式电极对面形的控制矩阵,运用最小二乘法求解分布式电压,才能准确地实现薄膜小变形面形的预知和控制。该方法是对薄膜大变形求解问题的有力补充。

　　参考文献:

　　[1]　金光,张亮,胡福生.大F数高分辨率空间望远镜光学系统[J].光学精密工程, 2007,15(2):155-159.

　　JIN G, ZHANG L, HU F SH. Investigation onsPACe optical of high F number and high resolution[J].Opt. Precision Eng.,2007,15(2):155-159.(in Chinese)

　　[2]　谢晋,阮兆武.光学自由曲面反射镜模芯的镜面成型磨削[J].光学精密工程, 2007,15(3):344-349.

　　XIE J, RUAN ZH W. Mirror form grinding offree-form surface of reflector mould core [J].Opt.Precision Eng.,2007,15(3):344-349.(in Chi-nese)

　　[3]　BEKEY I. Very large yet extremely light weightspace imaging systems [J].SPIE,2002,4849:17-27.

　　[4]　ANGEL R, BURGE J, HEGE K,et al.. Stretchedmembrane with electrostatic curvature (SMEC): Anew technology for ultra-lightweight space tele-scopes [J].SPIE,2000,4013:699-705.

　　[5]　MIHORIA D J.Test Progress on the ElectrostaticMembrane Reflector[R]. VirgiNIa: NASA, Lang-ley Research Center,1981.

　　[6]　齐迎春,金光,许艳军.空间薄膜反射镜面形设计及优化[J].光学精密工程, 2007,15(8):818-823.

　　QI Y CH, JIN G,XU Y J. The design and optimizeabout the shape of the space membrane mirror [J].Opt. Precision Eng.,2007,15(8):818-823.(inChinese)

　　[7]　CHEN X H,TANG M X,SHEN W M.Membranemirror deformed by electrostatic pressure [ J].SPIE,2007,6721:67210K1-67210K8.

　　[8]　CLAFLIN E S, BAREKET N. Configuring an elec-trostatic membrane mirror by least squares fittingwith analytically derived influence functions [J].Opt. Soc. Am.,1986,3(11):1833-1839.

　　[9]　GROSSO R P, YELLIN M J. The membrane mir-ror as an adaptive optical element [J].Opt. Soc.Am.,1977:67,399-406.

　　作者简介:

　　石广丰(1981- ),男,辽宁建昌人,博士研究生,主要研究方向为薄膜反射镜技术。E-mail:shigf-1981@tom.com

　　金　光(1958- ),男,吉林长春人,研究员,主要研究方向为星载一体化的研究。E-mail:jing@ciomp.ac.cn

　　刘春雨(1982- ),女,满族,吉林四平人,博士研究生,主要研究方向:光学检测技术; E-mail:Liucy.ciomp@tom.com

　　张　鹏(1985- ),男,汉族,福建龙岩人,博士研究生,主要研究方向:空间光学技术; E-mail:zpjg1021.student@sina.com