原子力显微镜的力曲线分析与转化

　　摘要：原子力显微镜测定的力曲线需转化为力位移曲线来应用。力位移曲线是以任意点为零点的，当研究粘附或者分子模型对比时，需要知道针尖样品间的作用力或确切的零点位置，这时需将其转化为力-距离曲线。本文首先从力曲线的测定原理得出了典型的力曲线，之后从理论上分析了力曲线、力位移曲线和力-距离曲线间的转化，从中得出了转化过程中需要的两个重要参量：灵敏度和零距离，并提出了确定方法。最后，利用 MATLAB 实现了曲线的自动转化。

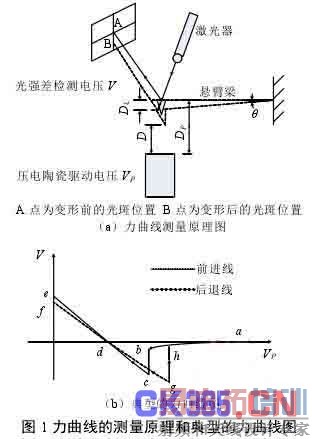
　　1986 年，G. BunNIng 在发明原子力显微镜(简写为 AFM)之初，它是作为成像工具的[1]。从 1988年起人们才开始研究利用 AFM 测定的力曲线[2]。测定的力曲线包含了很多有用的信息[2]，例如弹性、硬度和 Hamaker 常数等材料属性;剥离力、粘附力和摩擦力等表面力信息以及单分子特性等。因此力曲线分析技术应用领域广泛，人们也对此技术进行了深入研究。但是以往研究都是针对力位移曲线进行分析的[3]。当研究粘附力、粘附分子特性或者分子模型的对比等问题时，需要已知接触点或针尖样品间的作用力，而力位移曲线是以任意点为零点，反映的是悬臂梁偏移量的检测压差和压电陶瓷的伸缩量的关系图，不能够直接判定接触零点和作用力。这时需将力位移曲线转化为力-距离曲线，它是反映针尖样品间作用力相对于针尖样品间距关系的曲线。因此本文将讨论 AFM 对刚性材料样品(如硅片等弹性模量较小的样品)测定的力曲线与力位移曲线、力-距离曲线间的相互转化问题。从转化后的力-距离曲线中，可以获取针尖靠近、远离样品时所测各点的精确位置和作用力的性质以及发生的两次突跳的信息。

　　1 力曲线的测量原理

　　AFM 中，针尖固定在微悬臂的自由端，样品放置在扫描器上方，扫描器中的压电陶瓷管在驱动电压pV 的作用下，在垂直于悬臂梁的方向上运动。SPM 探头中的激光器发出激光，照射在探针的尖端背面，经过反射，落在光斑位置检测器上。光斑位置检测器上下部分的光强差产生了上下部分的电压差，通过测量这个压差V ，就可以得到光斑位置的变化量(如图 1(a)所示)。当样品垂直接近、远离悬臂梁的固定端时，微悬臂和样品间产生了相对位移。在这个过程中，微悬臂自由端的探针也在接近、甚至压入样品表面，然后脱离，此时 AFM 测量并记录针尖所感受的力，从而得到力曲线(如图 1(b)所示)。文献[4]对力曲线进行了详细的分析。

　　2 力、力位移与力-距离曲线间的转化

　　2.1 转化原理分析

　　从测量原理来看，力曲线是 AFM 检测悬臂梁偏移量的光斑检测器的检测电压差和扫描器中的压电陶瓷管驱动电压的关系图。但是实际中经常应用的是表示检测悬臂梁的偏移量的光斑检测器的检测电压差和压电陶瓷的伸缩量关系的力位移曲线。当研究某些问题时，需要使用针尖样品间作用力和针尖样品间距关系的力-距离曲线图。因此若要完成力曲线与力-距离曲线间的转化，需要实现纵坐标参数从压差到针尖与样品间作用力的转化及横坐标参数从压电陶瓷驱动电压到针尖与样品间距的转化。转化过程如图 2 所示。

　　悬臂梁在 F 作用下，发生形变，由位置检测器上的光斑点电压差来表示形变量

　　悬臂梁在外力和弹性力的作用下处于平衡状态，弹性力可以通过悬臂梁的偏移量和悬臂梁的弹性系数相乘求得，则针尖样品间的作用力为cF =kD。此时，纵坐标参量的转化完成。

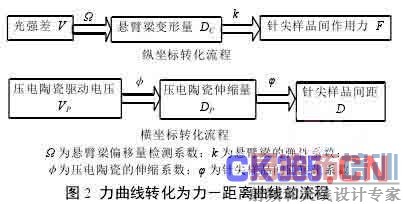
　　根据选用的压电陶瓷管的伸缩系数即可完成压电陶瓷的伸缩量与驱动电压间的转化

　　由图 1 可知，针尖样品间距为压电陶瓷伸缩量与悬臂梁偏移量的矢量和值p cD = D D，pD 在力位移曲线中是以任意点为零点的，未经标定。如果以标定零点开始计算压电陶瓷的伸缩量，则针尖样品间距为

　　从曲线转化分析中可见两个关键参量 和 c 是要解决的焦点问题，也是难点问题。

　　2.2 灵敏度和零距离两参数的确定

　　零距离为样品和针尖的初始接触点。实际测量中，由于粘附、表面特性等原因，接触点很难确定。理论上，零距离位置可以参考压电陶瓷的起始位置和悬臂梁偏移的平衡位置。但由于热漂移，AFM的设备部件尺寸会发生改变，这两个位置会随温度的变化而变化。因此，实际中，压电陶瓷的起始位置和悬臂梁偏移的平衡位置是不可取的。

　　力位移曲线分三部分：接触区、非接触区、零力线。对于刚性样品，接触区和零力线两部分都近似为线性。由于刚性样品在力的作用下变形很小，表面力随着距离的变化很少是线性的。当跟针尖样品相联结的其他部件刚度都很大时，悬臂梁受到的力是悬臂梁弯曲产生的线弹性力和由针尖样品产生的非线性表面力的总和。如果合力是线性的，产生的原因主要有两种情况：表面力为零，针尖样品间距很大时或者表面力的梯度很大，远远大于悬臂梁的梯度，这正是悬臂梁发生突跳的条件，即接触产生的瞬间。因此，定义力位移曲线中零梯度部分为零力线，梯度不是零的线性部分为针尖样品的接触区，接触区作用力为零的点为零点，零点处压电陶瓷的伸缩量为零距离。由图 1 可知，在接触区内，悬臂梁的偏移量值等于压电陶瓷的伸缩量，由力位移曲线中接触区的线性部分可以获取

　　可见这两个参数的确定不需要通过独立的方法求得，而可以从力曲线本身获取。图 3 为确定灵敏度和零距离的示意图。对于刚性材料，在忽略吸引力、表面性质和黏附的作用时，灵敏度为接触区的线性部分的斜率 ;标定零点即为两个线性部分的交点 0.

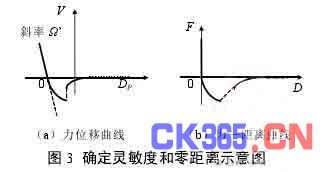
　　综上所述，两参数从力位移曲线中获取，灵敏度为接触区线性部分的斜率;零点为接触区线性部分和零力线延长线的交点，该点为转化后曲线的坐标原点;零距离为零点的横坐标。

　　3 力、力位移与力-距离曲线间的自动转化

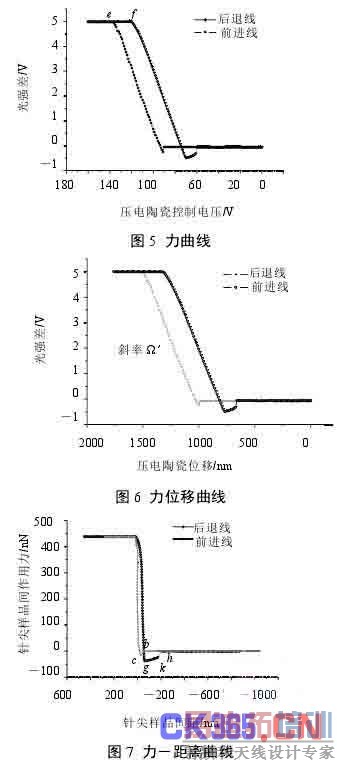
　　由于压电陶瓷的反转滞后很大，使前进线的末点 e 与后退线上始点 f 发生了偏移，使在曲线上对同一点的分析带来不便。因此，曲线转化过程中，需要消除仪器本身带来的滞后。为了精确计算灵敏度" ，需要取多点，利用最小二乘线性拟合方法来确定。由于接触区并非绝对的线性，在近似线性区域内选取数据点，减少误差。

　　大量测量点的转化运算、确定灵敏度时接触区斜率以及零距离的计算、前进线和后退线滞后的消除等问题使得手动转化曲线的过程及其繁琐。为了简化，需要实现曲线的自动转化。这将节省转化的时间，并使之通用化。根据上述分析的思路，用MATLAB 将之程序化。编写流程如图 4 所示。

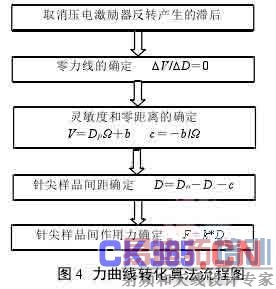
　　该软件主要实现的功能为：读入 AFM 获取的原始数据文档，绘制力曲线;将力曲线转化为力-距离曲线，并绘制出图像;对关键的粘附力和跳向接触力进行计算;对绘制图像和转化后的力-距离曲线的数据进行存档。

　　4 实验结果与分析

　　实验仪器采用型号为 CSPM4000 的 AFM，横向分辨率为 0.2 nm，垂直分辨率为 0.1 nm;最大扫描范围为 19 μm×19 μm;V 型悬臂探针的型号为CSC21，材料为 Si，悬臂梁的弹性常数为 1.0 N/m，谐振频率为 25 kHz。由上述方法对 Si 片进行测量，测定曲线及转化结果为图 5~图 7。从图 7 中可以直接获取在针尖靠近样品过程中各点的表面力信息和特殊点的具体位置。所关注的是测量过程中发生的两次突跳现象，前进线上在 b 点-40.81 nm 处针尖跳向样品表面，跳向接触力值为 16.0079 nN;后退线上在 k 点-160.3 nm 处针尖脱离样品，k-h 间剥离力为 24.32 nN，g-k 间粘附力值为 37.0977 nN。跳向接触力和粘附力同文献[5]测定的下跳变力、上跳变力相对应，曲线转化的计算值与文献[5]中的测定的下跳变力 16 nN、上跳变力 39.8 nN 基本吻合。AFM 实验测定的力曲线同典型力曲线有些差异，主要体现在：实验测定的力曲线的前进线的末端部分与后退线的起始部分有段水平线，这是因为压电激励器在连续加载的时，超出了检测器的检测范围，故输出值始终保持在量程值;此外，靠近线的末端点与后退线的起始点不重合，是由于扫描器由加载过程转为卸载过程时的位移误差造成的，这个位移误差是可以取消的;在后退线上，引力最值点与针尖样品的脱离点未重合，是因为相对样品刚度，悬臂梁的弹性系数选择较大的缘故。

　　从图 3 中可知 、 k、 φ、 四个参数影响曲线的转化。灵敏度 取决于激光二极管的激光点的形状和尺寸、测量介质的折射率，而且值随着 AFM 部件的温度的改变而改变，但是论文中灵敏度的确定是通过测定曲线本身计算得出的，因此该值比较精确;AFM 悬臂梁的弹性常数k 出厂值给定的是一个范围，对具体值没有明确的给出，因此在使用时需要测量得出准确值。悬臂梁弹性常数的获取除了从其几何尺寸直接计算外，常用的实验方法有热噪音强度法、共振频率质量因数法、参考悬臂梁法等;力位移曲线的转化是在压电陶瓷的位移跟电压是线性关系的条件下转变的，实际上，压电陶瓷也存在滞后特性，即位移跟电压是非线性关系。曲线转化中考虑压电陶瓷的特性这一点是曲线转化需要完善的地方; 的确定主要是零点的确定，本文解决了刚性材料条件下零点的确定，对于大变形的材料，未简化情况下的零点确定需要进一步研究。讨论的力曲线转化，在大多数应用中，是正确的。但是当违背了假设的应用条件时，就会出现线性部分的错误定位或线性部分数据误差较大等问题。 因此需要研究使用条件更宽泛的理论，使其适用于所有情况的曲线转化。

　　5 结论

　　讨论了 AFM 测定的力曲线与力位移曲线、力-距离曲线间的转化问题，从转化原理入手，分析出转化中的四个参量： 、 k、 φ、 ，其中 、 的确定是难点问题，涉及到了灵敏度和零点的确定：接触区线性部分的斜率为灵敏度，零点为接触区线性部分和零力线延长线的交点。由于手动转化曲线的过程及其繁琐，因此利用 MATLAB 软件实现了曲线的自动转化。此外，说明了四个参量对曲线转化的影响及转化过程中还需完善的地方。从力-距离曲线中可以直接获取探针靠近、远离样品过程中的相互作用力的性质以及突跳现象发生的准确位置、粘附力值和跳向接触力值，从而使得利用曲线获取信息更加便捷。AFM 对 SI 的例证中，计算值与已发表文献中值基本吻合，验证了力曲线转化的正确性。

　　参考文献：

　　[1]G. Binning，et al. Atomic Force Microscope[J]. Physical ReviewLetters，1986，56(6)：930-935.

　　[2]B. Cappella ， G. Dietler. Force-distance curves by atomic forcemicroscopy[J]. Surface Science Report，1999，34：1-104.

　　[3]H. J. Butt，et al. Force measurements with the atomic force microscope:Technique, interpretation and applications[J]. Surface Science reports，59(2005)：1-152.

　　[4]王德国. 利用原子力显微镜测量石英岩表面分子沉积膜的粘附力[J]. 石油大学学报(自然科学版)，1999，23(4)：53-55.

　　[5]杨勇. 基于 AFM 湿度对表面粘着力影响的研究[J]. 仪器仪表学报，2001，22(3)：65-66

　　基金项目：教育部科学技术研究重点项目支撑(NO.106018)

　　作者简介：张杰(1982-)，女，北京科技大学硕士研究生，主要研究方向为 MEMS 器件粘附研究。