数字鉴频器性能的测量限制

数字鉴频器(DFD)可为大范围的瞬时RF脉冲或连续波信号提供精确的频率测量数据。典型地它们覆盖宽广的带宽，如50到500MHz、0.5到2GHz、2到6GHz、6到18GHz，以及2到18GHz，但很少超过18GHz。实现18GHz以上DFD的一个主要限制因素是额外的相关器相位噪声。下面将回顾基本的DFD性能和限制，并介绍将可用性扩大到18GHz以上的设计。
图1显示了不同形式的DFD，取决于应用和性能需求。DFD是时更加复杂系统的基本构造单元，例如瞬时测频系统(IFM)接收机，其中还包含了门限电路、RF幅度量化器、RF包络脉宽测量能力和到达时间处理(TOA)。

DFD通常用来构成宽带电子战(EM)系统。图2是一个简化的框图，显示DFD微波组件，将一个EW系统简化到只有基本的内容，包括天线、线性放大器，和带通滤波器。DFD微波电路由RF限幅放大器、相位匹配RF功率分配器、和(典型地)7个相关器阵列组成，每个相关器带一个RF延迟线，延迟时间安排成二进制序列。每个微波相关器提供sin(θ)和cos(θ)视频输出，其中θ是延迟和非延迟RF输入间的相对相位。由于每个微波相关器有关的延迟时间是常数(秒)，延迟和非延迟相关器输入间的相对相位(θ)将会随RF输入频率的变化旋转。相关器输出是频率周期性的，周期由下式给出(输入频率范围需要产生2π弧度的旋转)：

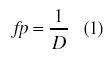
这里：fp=相关器频率周期(Hz)；D=延迟时间(秒)。

最短的RF延迟线(在图2中标为1X)在DFD的设计非模糊带宽上提供正好360度相位旋转的。最长的RF延迟线(在图2中标为64X)设定RF测量的精度和分辨率。中间的相关器(2X到32X)是用来解决1X和64X相关器之间的模糊的。1X到32X相关器带有比较器(TTL)输出，64X相关器是唯一采用模拟视频输出的相关器。如果DFD配置成只有比较器输出，简单的译码将产生8位输出数据字。仅使用比较器时，N个相关器将产生N+1个输出数据位。

在最长的延迟相关器上使用视频放大器和量化器使得频率测量精度扩展到12位或更高的输出分辨率。典型的7相关器阵列DFD提供12位输出频率数据字；已经生产了最少1个、最多10个相关器的DFD。由于VSWR和其它误差，相关器受相位测量误差支配。借助适当的解码，图2显示的基本设计允许每个相关器产生多达45度(与相邻相关器相比)的相位误差而不会导致模糊错误。

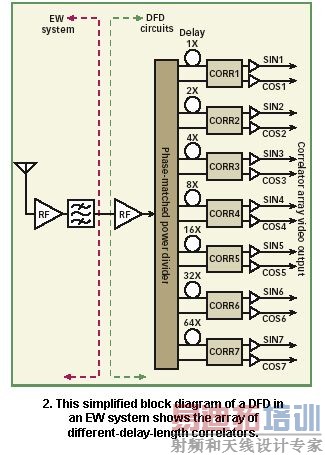
假如类似的设计只使用4个相关器(1X、4X、16X、64X)，相位余量将减少到22.5度。这个紧缩型设计(4比1)的问题在较高频段会变得明显。预期的高频相关器均方相位误差是6度。因此，三阶标准差是18度。在全部频率和温度范围内这非常接近最大允许相位余量22.5度，因此可能产生模糊错误。

由于RF频率测量精度和分辨率取决于最长延迟时间相关器的性能(例如64X)，集中精力于RF路径，包括RF前置放大器(决定系统噪声指数)和带通滤波器(决定噪声带宽)来改善性能是可能的。图2所示的相位匹配功率分配器被Wilkinson功率分配器，把RF输入分配到延迟和非延迟路径。相关器简单地将两路信号乘起来，把得到的视频信号低通滤波(图3)。使用此简单模型，RF输入频谱和Wilkinson功率分配器由图4所示。RF限幅放大器的作用暂时忽略。

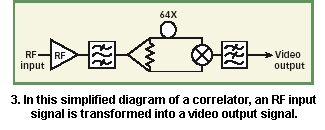
采用图3所示的系统模型，图4的输入谱，可以计算均方RF频率误差，是RF输入信噪比、相关器时间延迟、RF通带中心频率以及RF输入带宽的函数。

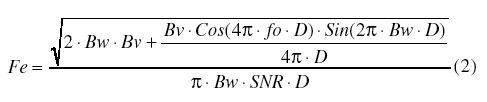
其中，Fe=频率均方误差(MHz RMS)
Bw=RF带宽(MHz)
Bv=视频带宽(MHz)
Fo=RF通带中心频率(MHz)
D=RF输入和相关器之间的延迟(µs)
SNR=输入信噪比(无量纲)

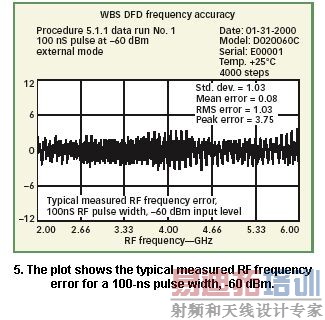
该公式使得在指定RF带宽下的频率测试精度时能计算需要的延迟时间。图5显示了典型DFD的频率测量精度。计算预见了高斯噪声分布，尽管图5显然显示了周期性误差。这些周期性误差是相关器微波电路中的VSWR效应带来的。除了热噪声带来的测量频率误差，存在着三种显著的噪声源：相关器VSWR、量化噪声和模糊误差。

微波相关器内部VSWR产生相位测量误差：这是热噪声误差的加性误差，呈现在RF噪声到视频噪声的转换中。典型地2到16 GHz相关器有4度。6到18 GHz相关器产生大约6度均方相位误差。

由于DFD产生数字输出，它受量化误差影响，与平均频率测量单元宽度成正比。量化噪声可通过增加DFD频率测量精度来减少。单元宽度与量化噪声的关系为：

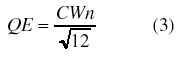
这里：QE=量化噪声(MHz，RMS)；CWn=常见输出数据频率单元宽度(MHz)

在解码时，如果相邻相关器相位误差超出最大允许相位余量，模糊误差就产生了。该误差比什么都严重，因为其值很大且重复。例如，DFD设计用于产生1MHz频率精度，而模糊分辨率的崩溃可能产生128MHz、256MHz或其它频率测量精度之二进制整次幂的误差值。早期DFD设计采用4比1相关器延迟，相位余量限制为22.5度。如果以此实现6到18GHzDFD，三倍标准差达到18度，非常接近相位余量极限。由于此原因，早期DFD设计通常规定允许产生一些模糊误差。现代设计采用2比1相邻相关器延迟，不允许在设计动态范围内出现模糊误差。

所有这些误差源可概括在单一曲线中，原型DFD设计的性能可在给定的RFSNR范围内计算和评估(图6)。有一个特别的分析程序考虑关键的设计参数，包括无模糊带宽、RF带宽、视频带宽、相关器数目、输出频率测量精度、相关器相位误差估计，以及计算RF噪声到视频噪声(在等式2中)。这些误差以平方和开方来计算。累加所有这些误差源使得程序能将预期的RMS误差作为输入RF SNR的函数来绘图。计算了模糊误差边界，使用等式1在累计相位误差超过23.08度时将频率误差转换为相位误差并设定RF SNR边界。这对应于1.95倍相位标准差，或者以5%的概率超出45%的相位余量。

热噪声误差曲线在0 Dbr FSNR区域有一个双曲线。这考虑了负的RF输入SNR，RF限幅放大器(图2)相对于噪声电平将信号抑制了1.05dB.当RFSNR为正时，同样的功能将噪声压低3dB。

为了验证图6的数据测试了一个产品化的DFD，在2到6GHz设计带宽上采用了500个频率步，1dBRFSNR步长，从+15dB到-10dB。结果显示在图6曲线F中。在较高的SNR输入区域，结果比预测略好，表明相关器VSWR比预测略好。随着输入SNR降低，预期曲线和测量曲线逼近一致。小于-2dBSNR时，随着模糊误差边界的逼近，测量误差变大。当接近-10dBRFSNR时，输出数据失去了与RF输入的任何联系，DFD基本上变成了随机数发生器。

要达成这样的结果需要在系统天线和DFD之间竭力控制RF增益。例如，考虑DFD之前的RF增益路径在整个频带上理想地平坦，只在一个小区域相对于整个工作频段有2dB衰落。在此2dB衰落区域，输入系统的RF信号必须增加2dB以充分利用DFD的灵敏度。为此原因，要考虑系统中安装的DFD所需的全频带灵敏度，对应于DFD最小操作RFSNR，加上DFD之前的峰峰增益变化。

输入了设计无模糊带宽和相关器数目，程序计算最长RF延迟线的长度(64X相关器)为12.50纳秒，如图6之G所示。进一步指定视频带宽为10MHz，对应于10到90%视频上升时间为35纳秒，程序将计算最小RF触发脉冲宽度H，作为最长RF延迟和视频上升时间之和末尾47.5纳秒。这是最小的RF脉冲宽度，如果DFD由RF输入包络同步触发。如果DFD是同步设计，100%截获概率(POI)所需的最小RF脉冲宽度为最小的RF脉冲宽度和时钟周期之和。

为了验证POI对RF脉冲宽度概念，将图7的数据输入给2到GHz DFD。在此情况下长延迟是7.81纳秒，系统采样时钟是40MHz。相关器输出视频带宽设置成10MHz。最小触发RF脉冲带宽计算出是42.81纳秒；100%截获概率(POI)RF脉冲宽度为67.81纳秒。

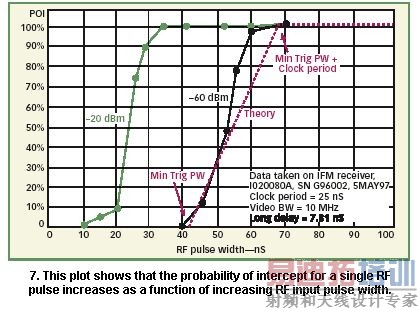
观察图7，当施加一个门限输入信号时(-60dBm)，100%POI到最小触发RF脉冲带宽转换几乎是线性的。增加RF输入信号电平改善短脉冲的POI，主要是由于在高RF输入电平时的视频展宽造成的。

最后回到图6，该计算机程序也计算最低RF SNR，这样，给定输入频率是一个输出频率单元的中心，保证数据报告的最小RF输入SNR是在单元内部，概率为0.9。这在图6中显示为I。

该专有的计算机程序提供了DFD设计的巨大推动。一旦所需的RF带宽和输出频率精度及分辨率确定了，就能够计算所需的延迟时间。然后将得到产生所需输出的延迟线数目。

尽管触发式DFD设计中，频率数据由RF包络触发，形成POI和最小RF脉冲宽度的最佳组合，大多数现代DFD是同步的而非触发的。在同步DFD设计中，RF频率以固定间隔连续采样。这允许同步频率测量数据与RF振幅和到达角(AOA)数据同步。同步设计也支持DFD内部的RF SNR估计，这样，除了提供测量的频率数据，DFD同时在RF频率采样时估计RF SNR。RF SNR的瞬时估计消除了噪声浮动门限的需求，还支持其它特性，如先进的脉冲上的脉冲、或者连续波上的脉冲，以及多径对消。