投射离焦三维测量方法

　　1　引　言

　　离焦三维测量是通过比较不同摄像参数下两幅物体图像的离焦程度来获取物体的三维深度信息的。由于采用了同轴照明,所以消除了三角测量的阴影问题以及双目视觉和运动视觉的闭塞问题。它不像调焦三维测量那样需拍摄大量的物体图像[1]。离焦三维测量具有计算简单,便于进行实时测量的优点,是一种很有潜力的测量方法。离焦三维测量方法已被广泛地应用于物体探伤、物体识别、机械制造、人工智能等领域。离焦三维测量可分为主动三维离焦测量和被动三维离焦测量。主动三维离焦测量方法具有较高的精度;被动三维离焦测量测量精度低,但系统简单,在无法控制测量环境时具有突出的优势[2]。

　　传统的主动离焦三维测量是通过改变摄像系统的数值孔径、摄像面的位置、摄像镜头的焦距、或这些参数的组合来实现三维测量的[3]。改变摄像系统的数值孔径将会改变传播到摄像面的光能量。当数值孔径变小时,摄像面上的光强将会很弱,拍摄的图像有较大的噪声。改变摄像面的距离将会改变物体图像的大小,使相对模糊的计算变得困难。尽管可以采用图像插补方法和远心光路方法来解决对应点的问题,但插补方法会产生光滑效应,而用远心摄像透镜需要附加一个光阑,这个附加光阑将会极大地减小投射到摄像面上的光能量,限制了其使用围[4]。改变摄像镜头的焦距同样会改变物体像的大小。为了解决离焦测量中的这些问题,本文提出一种新的主动离焦三维测量方法,这种方法的要点是通过改变投射光路的参数(投射光路的焦距、投射模板的对焦平面位置、投射系统的孔径光阑以及它们的组合)来进行离焦三维测量的。采用这种方法进行主动离焦三维测量可以保持系统的摄像光路的参数不变,只需改变投影系统的参数,拍摄两幅不同投射参数的物体图像就可以找出该处的物体深度,实现物体的主动三维离焦测量。

　　在投射光路中实现主动离焦三维测量有如下两个优点:首先它不仅消除了传统方法中的图像放大率的变化问题,而且也消除了由于改变摄像光路中的孔径光阑引起的光强的变化问题;其次是增加了主动离焦三维测量的可选办法,扩大了主动离焦三维测量的使用范围。在投射系统内实现物体的三维离焦测量也带来了一个新的问题,由于需改变投射系统的投射参数,因而会导致同一物点相应的两次投射的位相变化,两次投射的相移将可能引起测量误差。本文首先建立投射光路来实现主动三维测量的离焦模型,在这个模型的基础上找到实现三维测量的方法,然后分析投射模式相移变化对三维测量的影响。

　　2　原理

　　2.1　正弦光栅投射下的离焦模型

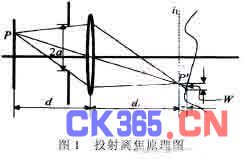
　　基于投射的离焦模型如图1所示。从模板上的P点发出的光经半径为a的孔径光阑和投射透镜后,聚焦在投射模板的对焦平面i1上的P′点,然后照射在距对焦平面距离为z的物体表面点W上,在通过照射点W并垂直于z轴的平面K上成一个半径为R的圆形光斑。如果投射模板到投射透镜的距离为d,投射透镜到模板的对焦像面i1的距离为di,投射透镜焦距为f,则它们之间的关系为

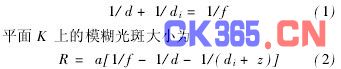
　　由式(2)可知,只要知道照射在K平面上的光斑半径R,就能求出W点到投影系统的距离,得到物体表面点的深度。由于模糊光斑是摄像系统的对焦平面i1上的P′点传播到物体表面上的光强分布,根据点扩散函数的定义,它是投射系统的对焦平面传播到K平面上的点扩散函数,所以称为离焦点扩散函数。如果光斑在半径R范围内的光强是均匀分布的,则它是离焦点扩散函数的Pillbox模型。但实际投射系统存在衍射和像差,照射在K平面上的光强分布不再是一个均匀的圆斑,这时离焦点扩散函数的模型需要根据具体分布确定。如果平面K上的光斑具有圆对称分布,则可采用高斯模型来描述。为了统一,对于所有离焦点扩散函数模型来说,都可以把它表示为h(x,y;σ)的形式,其中σ是描述离焦点扩散函数的分布情况的参数,被定义为

　　式中:C是K平面上光斑覆盖的区域;(x,y)是建立在平面K上的坐标,因为物体是三维的,对焦平面到物体表面不同点的距离不同,在物体表面上由对应K平面得到的光斑分布也不同,在确定离焦点扩散函数模型的情况下,知道了σ,就知道了对应的离焦点扩散函数。所以可以用σ来表示离焦点扩散函数。

　　离焦扩散参数σ值决定于点扩散函数的模型,它描述光斑在平面K上的弥散情况,扩散参数与Pillbox模型中的半径R之间具有如下关系:

　　k的数值决定于离焦点扩散函数的模型[5],知道了对焦平面传播到物体表面的离焦点扩散函数(该点的K平面),就可以计算出摄像面上的光强分布。

　　2.2　投影离焦系统中物体在摄像面上的光强分布

　　基于投射离焦三维测量的光路如图2所示。透过率函数为p(x,y)的投射模板经半径为a的投射孔径光阑和投射透镜后成像在对焦平面i1上(也可在i2上)。如果对焦平面传播到物体表面的点扩散函数为h(x,y;σ),则在CCD上拍摄到的物体图像可表示为

　　式中:f(x, y)是位于(x,y)位置的物体纹理分布;h(x,y;σ1)是对焦面i1传播到物点Q并通过Q点的K平面上的点扩散函数分布。在式(5)的推导过程中使用了这样一个事实:一般情况下,物面与K平面不重合,物面上的离焦点扩散函数是K平面上离焦点扩散函数分布的一个投射变换,所以它们的分布不同。尽管物面上的光强分布是离焦点扩散函数分布与模板透过率函数p(x,y)的卷积,但在计算像面上的光强分布时需要将物面上的离焦点扩散函数反向投射回像面。由于摄像面的轴线与K平面的轴线都垂直于光轴,所以式(5)中的离焦点扩散函数分布就是K平面的点扩散函数分布。

　　要想式(5)成立,要求成像透镜的景深很大,使物体成清晰的像。由于不同深度具有不同的离焦点扩散函数,因此它是一个空变系统,严格地讲不能写为式(5)的卷积形式,但在测量点附近的小区域内,离焦点扩散函数在该区域内可认为是不变的。因此式(5)在测量点附近的小区域内是成立的。只要计算出离焦点扩散参数随坐标的变化关系,就可以根据式(4)计算出物体的深度。要想得到扩散参数,需要消除式(5)中的纹理的影响。为此,可在不同投射参数下拍摄两幅物体图像,把它们分别记为i1(x,y)和i2(x,y)。根据式(5),它们与投射模式、物体表面纹理和离焦扩散参数的关系为

　　由于投射模式的透过率分布是预先知道的,只要预先标定好投射系统的离焦点扩散函数,从式(8)中计算出扩散参数之比,就能测量出物体的深度。由于式(8)右边是一个卷积关系,直接用该式计算物体深度是很困难的。

　　当采用正弦光栅投射时,光栅的数学表达式为

　　如果透射正弦光栅的频率足够高,则式(10)和式(11)中的各级频谱之间是相互分开的,选取合适的滤波器,将其中的某一级频谱过滤出来(非0级),比如正一级,就可得到两幅图像的一级频谱为

　　式中,I1(u,v) "1,I2(u,v) |1分别是拍摄的两幅图像的一级频谱。可以看出,在测量点的空间邻域内,两物体图像的一级频谱在任意频率处之比等于投射频率处的两对焦平面离焦传递函数之比。由于图像噪声和物体表面纹理的随意性,使用任一个频率计算一级频谱之比是不可靠的。在主动投射下,在拍摄图像的频谱中投射频率占有支配地位,因此局域频率的频谱在投射频率处最为可靠[3]。为此选择了投射频率来计算式(12)左边的值,这样式(12)可变为

　　式(13)左边的物理意义为:在正弦光栅投射下,物体某点两投射图案的相对模糊(扩散函数在投射频率处之比)等于物体在该处拍摄图像的一级频谱在投射频率处之比。根据式(5),在正弦光栅投射下拍摄的物体图像可表示为

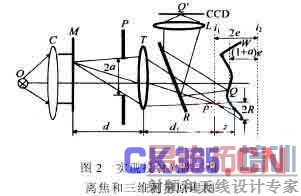
　　从式(14)可以看出,物体在正弦光栅投射下的图像是被调制了的正弦光栅,在位置(x, y)处的一级频谱在投射频率处的值就是式(14)中的B(x,y),它正是该图像在(x, y)处的调制度值,式(13)左边正是两正弦光栅调制图像的调制度在(x,y)处之比。因此,可以先通过傅里叶变化直接求出图像的调制度分布,然后再根据式(13)求出物体的深度分布。计算方法与文献[6]中的深度计算方法相同。图3是采用投射三维离焦测量方法的流程图。

　　2.3　实验装置

　　本实验的光路图如图2所示,由光源O、集光镜C、正弦光栅模板M、投射孔径光阑P和投射透镜T组成的投影仪将投射出的正弦光栅经分光镜R后分别成像在物体前的i1平面和物体后的i2平面,被投射了正弦光栅的物体通过分光镜R被成像在CCD靶面上。实验中,使用的光栅空间频率为2对线/mm,物体是一个高度为21mm的阶梯圆台,顶部的小圆台高为1mm,阶梯圆台被放置在一个平面上。图4是被投射了正弦条纹的物体图像。实验中,投射透镜的焦距为25mm,摄像透镜为尼康摄像镜头(焦距为24mm)。在整个实验中,除了调整投射透镜与正弦模板的距离来改变光栅成像面的位置外,其它部分都保持不同,同时尽量保持照明光路和成像光路同轴。

　　3　图像处理和实验结果

　　通过改变投射透镜到投射模板的距离,使它的像分别处在i1和i2平面,分别拍摄这两个位置的物体图像,然后将它们进行快速傅里叶变换,再分别进行滤波,过滤出一级频谱。为提高测量精度,在滤波时尽量选用带宽较大的空间滤波器,但同时应确保过滤出的频谱没有0频分量和低的高频噪声。在得到两幅图像的一级频谱后,对它们进行逆傅里叶变换,就可得到物体的调制度分布,通过对应点调制度之比就可得到物体的深度分布。图5是采用本文所提出的调制度计算方法得到的物体深度分布。

　　实验表明,使用改变照明光路参数的方法也能够较为准确地恢复出物体的三维形貌,在本文所提出的实验条件下,用该方法恢复出的物体深度的标准差小于2.8%。

　　从上面的结论可以看出,与改变成像光路参数一样,通过改变投射光路的投射参数来进行离焦三维深度测量,消除了成像光路方法的图像放大率问题,为离焦三维测量提供了一种新的方法。

　　参考文献:

　　[1] Pentland A P. A new sense for depth of field[J]. IEEE Trans onPAMI 9, 1987,(4): 523—531.

　　[2] Girod B, Scherock S. Depth from focus of structured light[J].Proc of SPIE, 1989, 1194: 209—215.

　　[3] Masahiro Watanabe. A study on efficient range sensing with thedepth from defocus method[EB/OL]. http: //www.core.t.u_tokyo.ac.jp/thesis/old/thesis980521.html, 1997.

　　[4] watanabe M, Nayar S K. Telecentric optics for computational vi-sion[J]. IEEE Trans on Pattern analysis and Machine Intelligence,1997,19(12):1360—1365.

　　[5] Subbarao M. Parallel depth recovery by changing camera parame-ters[A]. Proc of Intl Conf on Computer Vision [C]. TarponSprings, Florida, 1988.

　　[6]王华,苏显渝,邵双运,等.主动离焦测量的调制度全局计算方法[J].光学技术,2004,30(3).

　　作者简介:王华(1962_),男,重庆市人,重庆师范大学物理学与信息技术系、重庆医科大学生物医学工程系副教授,博士,主要从事信息光学方面的研究。

　　E-mail:wantcop@163.com