基于正交多项式的称重仪表非线性校正算法

　　摘  要： 针对称重仪表检测电路中输入与输出值之间存在非线性关系的特性，在比较了几种非线性校正方法的基础上，给出了一种易于微处理器实现的正交多项式的非线性校正方法，求取称重仪表检测电路的非线性特征，实现了称重仪表的非线性校正。同时讨论了该算法的原理、校正参数的空间复杂度和算法的时间复杂度，从而论证了此算法在简单微处理器上的可用性，并以3阶多项式为例介绍了该算法的实验效果。实践表明，该算法简单实用，效果较好。

　　关键词： 正交多项式；传感器；非线性校正

　　称重仪表是电子衡器的心脏部件，它融合了当今先进的信息技术和计算机技术，在工业过程控制和贸易结算等方面得到了广泛应用。随着微型计算机技术和嵌入式系统的迅速发展，现代测控系统对称重仪表准确度、稳定性和工作条件等方面提出了更高的要求。然而，由于电子元器件性能参数的离散性、稳定性和敏感性等因素的影响，使得压力传感器的反馈信号X和被测物体的质量Y不是标准的线性关系。因此，需要对称重仪表增加非线性校正环节。

　　非线性校正可以通过模拟电路来实现，但是模拟电路的接入不但增大了仪表的体积和成本，而且还会带来新的非线性因素。随着智能化仪表的发展，软件非线性校正方法得到了广泛应用。目前，非线性校正方法主要有遗传算法[1]、神经网络法[2]、支持向量机法[3]、插值法[4]、函数拟合法等，这些方法取得了良好的校正效果，但是由于算法的复杂性对称重仪表的处理器速度和存储器容量提出更高要求，使得其中一些算法在普通的智能仪表中实现困难。鉴于这个原因，参考文献[5]和参考文献[6]分别采用了分段插值法和最小二乘法拟合曲线函数达到了较好的效果。然而分段插值法虽然算法简单，但是需要保存的浮点数参数随着插值节点的增加而增多，对于存储空间有限的称重仪表来说浪费了过多的资源；最小二乘法拟合曲线函数虽然算法成熟，需保存的参数也不多，但是在工程实践中经常会出现参数差异较大的病态方程，使得出的数据不可靠。本文基于正交多项式构造了一个称重仪表的非线性校正系统，既降低了曲线拟合算法的运算复杂度，又节省了存储空间，提高了称重仪表的可靠性和稳定性。

1 称重仪表的非线性校正原理

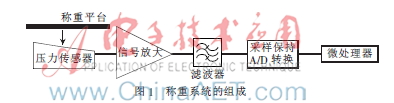
　　如图1所示，称重仪表由称重压力传感器、放大电路、滤波器、采样保持器、A/D转换电路、微处理器及相关附属配件组成。其中，微处理器和A/D转换电路是称重仪表的核心部件，负责将压力传感器反馈的模拟量转换为数字量，同时，依据计量算法将此数字量转换成称重物体的称重值。

　　软件实现称重仪表的非线性校正就是在测量系统中为被测物重量与电信号输出之间构造理想的非线性函数关系。假设被测物体的质量为m，传感器及其采集电路的电信号输出为v，其校正模型表示为v=g（m）。在A/D转换之后增加一个由微处理器实现的非线性校正环节y=f（v），使补偿后的输出y与被测质量u之间具有良好的线性特征，即：

　　Y=u=g-1（m）（1）

　　由式（1）可知，当非线性校正环节为称重仪表的反函数时，则可实现称重仪表输出的非线性校正。由于g（m）函数具有高度的非线性，因此f（v）很难直接获得。本文利用正交多项式构造了称重仪表的拟合函数，实现了称重仪表的非线性校正。

　　2 正交多项式的非线性校正原理

　　称重仪表的非线性特征可以用m次多项式的非线性曲线来逼近，该多项式方程通过构造正交多项式[7]来获得。对于称重仪表通过静态实验标定获得的数据点（xi，yi）（i=1，2，…，n），此处x为称重仪表通过A/D转换后获得的数字量，y为称重值，选取一组在这些点上的正交的多项式函数系{Qi（xi），j=0，1，…，m}作为基函数组，其中Qi（xi）是j次多项式。拟合多项式记为：

　　式（4）中，k，j=0，1，…，m，一般m远小于n。

　　根据格拉姆-施密特正交化方法，构造给定点上的正交多项式Qj（x）（j=0，1，…，m-1）的方法如下：

　　Q0（x）=1Q1（x）=（x- 琢0）Qj+1（x）=（x- 琢j）Qj（x）- 茁jQj-1（x）（5）

　　其中：

　　通过以上递推公式，可以将式（2）推导为m次多项式的一般形式：

　　将q0Q0（x）项展开后累加到式（7），得：

　　当j=1时，令Q1（x）=t0+t1x，显然，t0=0，t1=1。由递推公式（3）得：

　　将q1Q1（x）项展开后累加到多项式（7）中，即有：

　　a0+q1t0 圯a0

　　q1t1 圯a1

　　对于j=2，3，…，m，逐步递推Qj（x），根据式（5）有：

3 算法设计

　　3.1 校正方程参数的数据结构和空间复杂度

　　由式（7）可知，m阶正交多项式的非线性校正方程常驻内存参数由m+1个多项式系数组成，即a0，a1，…，am，在算法中将这些参数定义为一个数组a[0]，a[1]，…，a[m]。在称重仪表称重过程中实时用到这些参数进行非线性校正。如果使用3阶正交多项式，只需要4个浮点数，一般的微处理器完全可以支持。

　　由式（14）可以看到，m阶多项式系数的计算过程中还需要3个长度为m+1的数组（即公式中的s、t、b）作为临时辅助变量，在算法中，分别定义为s[m]、t[m]、   b[m]，其中m=0，1，…，m，共需3×（m+1）个浮点数。此外，通过算法优化，可以将式（3）和式（6）中的3个长度为m+1的参数值（即公式中的α、β、q）缩减为3个变量重复使用，在算法中定义为α、β、q三个浮点数。

　　同时，由递推公式（3）和（6），n个数据采样点也要占用2n个浮点数分别存放采样值x和称重值y作为临时变量。在算法中定义为长度为n的数组x[n]、y[n]。

　　综上所述，构造n个采样点的m阶正交多项式所需临时变量的空间复杂度为：

　　2n+3（m+1）+（m+1）+3

　　由此计算，如果构造10个采样点的3阶正交多项式，构造过程共需39个浮点数，其中，临时变量35个，常驻内存变量4个。如果微处理器的存储内存资源不能达到要求，可以用离线方式构造正交多项式，只将多项式系数保存在称重仪表中在线使用。

　　3.2 正交多项式校正算法流程和时间复杂度

　　以下给出m阶正交多项式算法流程，其中m≥3。

　　算法预备：通过称重仪表静态标定，获取n个采样点（xi，yi）分别存入数组x[n]、y[n]，并定义其他上述相关变量。

　　（1）当j=0时，依据式（8）求取式（2）中的q0，并且将q0的值放入多项式系数a[0]中保存，依据式（9）计算α0并保存到α中，令b[0]=1。

　　（2）当j=1时，t[0]=-α0，t[1]=1。依据式（10）~式（12）计算式（2）和式（5）的α1、β1、q1并分别保存到变量α、β、q中。同时，更新多项式系数a[0]=a[0]-α×q，a[1]=q。

　　（3）当j=2，3，…，m时，依据式（14）和式（15）依次进行以下运算和变量更新：

　　①s[j]=t[j-1]；

　　②s[j-1]=-α×t[j-1]+t[j-2]；

　　③当j≥3时，依次对k=j-2，j-3，…，1进行如下运算：

　　s[k]=α×t[k]+t[k-1]-β×b[k]；

　　④s[0]=-α×t[0]-β×b[0]；

　　⑤当k=j-1，j-2，…，0时，由式（3）、式（6）计算当前的αj、βj、qj并分别保存到变量α、β、q中，在下一次循环中使用；

　　⑥当k=j-1，j-2，…，0时，更新如下变量：b[k]=t[k]；  t[k]=s[k]；

　　⑦由式（15），更新多项式系数a[j]=q×s[j]；

　　⑧由式（15），更新当k=j-1，j-2，…，0时多项式系数a[k]=q×s[k]+a[k]。

　　（4）保存正交多项式系数a[0]，a[1]，…，a[m]。

　　可以看出，构造正交多项式的时间复杂度主要集中在步骤（3）。其中，计算①、②、③中s[j]的累计时间复杂度为（m+2）（m-1）/2，⑥、⑦、⑧的计算可放在同一循环中，其时间复杂度为（m+2）（m-1）/2。除此之外，计算⑤中αj、βj、qj还需要n（m+2）（m-1）/2次的运算。总的时间复杂度为：

　　（n+1）（m+2）（m-1）/2

　　当用10个采样点构造3阶正交多项式时，其时间复杂度为55，这个值对于一般的微处理器来说完全可以支持。

　　4 实验结果分析

　　4.1 实验方案

　　为了检验正交多项式对称重仪表输入电压值u和重量值x的实际逼近效果，实验分两步进行：

　　（1）选取0~380 kg作为称重仪表的量程，每隔40 kg测量一次，一共获得10个数据作为数据标定点（xi，ui），结果如表1所示。用这10个采样点构造3阶正交多项式，获得多项式系数。

　　（2）以20 kg为间隔，在0~380 kg之间测量电压值作为测试点，共获得20个测试点并代入正交多项式进行检验（结果如表2所示）。

　　最后计算所有测试点的相对误差，分析实验结果。

　　4.2 实验结果

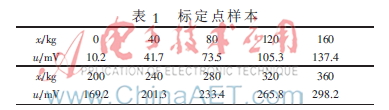
　　由表1所列的数据标定点，按照正交多项式构建方法求得正交多项式系数为：a0=12.8278，a1=1.2659，a2=  -4.3691×10-5，a3=-2.8491×10-8，从而求得此称重仪表非线性校正环节的表达式为：

　　w（u）=-12.8278+1.2659u-4.3691×10-5u2-2.8491×10-8u3（16）

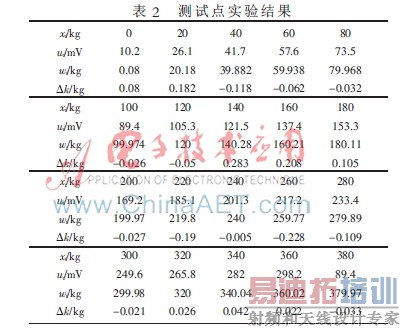
　　将表2中的20个测试值ui代入式（16），求得实际测量值wi，从表2可以看出，最大误差为0.283，最小误差为-0.005，误差的算术平均值为0.003。

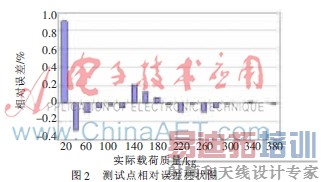
　　图2是根据相对误差计算公式式（17）绘制的各称重测试点相对误差直方图。从图中可以看出，所有试验点的相对误差均未超过1%，19个相对误差测试点中，相对误差最大的是称重载荷最小的点，其相对误差是 0.9%，其次是第二个测试点，相对误差是0.3%，其他测试点的相对误差逐渐减小，最大不超过0.2%，平均相对误差0.03%，当称重载荷大于300 kg时相对误差小于 0.01%，其精度完全符合测试要求。从相对误差的变化趋势上看，当称重载荷质量较小时，相对误差较大；称重载荷越大，相对误差呈锯齿状减小。这说明正交多项式与称重仪表的实际值很接近，误差值很平均，称重越重，相对误差就越小。因此，在精度要求较高时，正交多项式校正算法更适用于接近满量程的应用。

　　δ= 驻k/xi×100%（17）

　　本文针对称重仪表采集信号输入和称重值输出呈非线性特征，在称重系统中加入了由软件方法实现的非线性校正环节，利用正交多项式拟合法进行了非线性补偿。实验结果表明，称重仪表通过非线性校正之后最大相对误差小于1%，称重越大，相对误差越小，其校正效果能达到实际需要。

　　实际应用中也表明，正交多项式非线性校正技术算法简单可靠、运算过程中所需存储器容量较小，易于在只配备简单微处理器的称重仪表中实现。在实际应用中提高了称重计量准确性和灵敏度，降低了误差，具有广泛的应用价值。

　　参考文献

　　[1] 范铠.传感器软件非线性校正方法综述[J].上海计量测试，2004，31（2）：8-12.

　　[2] 陈俊杰，芦俊，黄惟一.基于遗传神经网络的传感器系统的非线性校正[J].仪器仪表学报，2003，24（2）：201-204.

　　[3] 刘涛，王华.传感器非线性校正的遗传支持向量机方法[J].电子测量与仪器学报，2011，25（1）：56-60.

　　[4] 刘少强，黄惟一.基于插值计算与优化的铂电阻非线性校正方法[J].仪器仪表学报，2003，24（2）：215-217.

　　[5] 文其知，戴永.智能仪表非线性自动校正方法研究[J].自动化仪表，2009，30（6）：75-78.

　　[6] 魏国，王昕，雷苗，等.基于B样条递推最小二乘的温度传感器非线性校正[J].传感器与微系统，2008，27（12）：54-56.

　　[7] 徐士良.计算方法[M].北京：人民邮电出版社，2009.