光纤电流传感系统影响因素分析

摘  要: 基于法拉第效应利用琼斯矩阵建立双螺线管式光纤电流传感系统的完整理论模型，对偏振分束器的透光轴夹角误差、固有圆双折射误差、线性双折射误差等影响系统测量准确度的各种误差进行仿真研究。研究发现：固有双折射引起的传感系统误差最小，其次是偏振分束器的透光轴夹角误差，线性双折射引入的测量误差最显著。本文光纤电流传感头采用低双折射光纤进行制作可以有效降低弯曲等因素带来的线性双折射。
关键词: 光纤电流传感器； 误差； 线性双折射； 低双折射

    地铁杂散电流的有效监测能为地铁杂散电流的腐蚀判断及维护提供有力的依据[1]。随着人们安全意识的不断增强，对地铁杂散电流的监测提出了越来越高的要求，传统的地铁杂散电流监测设备愈来愈显示出其局限性，这就对新型的地铁杂散电流监测技术的探索和研究提出要求。光纤电流传感技术的快速发展，特别是其具有良好的电气绝缘性能、卓越的抗干扰能力及极快的频响等特点使其具有极大的研究和应用前景，但其输出信号幅值较小、光路设计和制造复杂又限制了其广泛应用。随着现代新光学材料、新光纤材料、新加工工艺的研究和应用，集成光学技术的不断进步及光纤处理技术的发展为光学电流传感器的应用提供了巨大的可能性[2-5]。
    本文研究的全光纤电流传感器属于偏振态调制型光纤传感器，其基本理论是Faraday效应。外磁场会导致光波发生偏振态的改变，这是Faraday效应的本质。有许多种研究光的偏振及偏振系统的方法，琼斯矩阵就是其中较为有效的方法之一。可以使用Jones矩阵来表示偏振系统中的各种偏振相关器件的特性。现有大量报道对一些偏振器件进行了研究分析并通过解析求解出该器件的Jones矩阵[5]，但是都对琼斯矩阵进行了简化，也就是省略掉了其存在的公共相位这一项。本文对光纤电流传感系统中的各个偏振器件的琼斯矩阵进行了求解并分析各个器件的相位误差对整个光纤电流传感系统的影响，所以，对光纤电流传感系统的各个器件的完整琼斯矩阵进行了解析求解。


    光纤固有圆双折射引入的偏转角φT变化时，光纤电流传感器响应随法拉第转角的变化关系如图3所示，随着线性双折射引入的相位延迟的增加，导致传感器响应趋于平缓，使系统灵敏度下降。且当线性双折射引入的相位延迟>π/2时，传感系统对法拉第转角变化的响应明显较小，当相位延迟π时，传感系统响应基本为零。从图中可知，当固有圆双折射引入的偏转角较小(θP≤π/60)时，对于某一法拉第转角，系统响应误差较小，随着夹角误差θP的增加，系统响应误差相应增大。

  
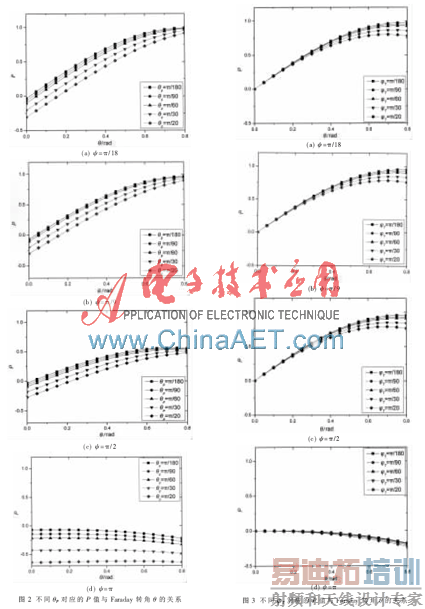
　    当系统存在一定的线性双折射时，光纤电流传感器响应随Faraday转角的变化关系如图4所示。随着线性双折射引入的相位延迟的增加，曲线趋于平稳，传感系统响应灵敏度明显下降。当线性双折射引入的相位延迟增大到π时，传感系统响应基本为零。
2.4 减小线性双折射的方法

    从上述分析可以看出,线性双折射引入的相位延迟对传感系统灵敏度的影响最大。因此只要能够有效减小或消除线性双折射，其他影响因素就比较好处理。
     本文利用低双折射光纤来降低线性双折射引起的误差，低双折射光纤的几何截面相对于普通光纤来说圆度比较好，而且其光轴与光纤圆度的轴线比较吻合。因此当利用该种光纤来传输一段相对较长距离的光波时，其线偏振光能较好地保持其偏振态。主要是因为低双折射光纤中传输光波的两个相互垂直的基模其传输速度基本上能保持一致，这样即使传输一定距离后也不会产生相位差。
    经过分析得到主要结论如下：
    (1)系统响应误差随偏振分束器的透光轴夹角误差的增大而相应增大，系统响应随固有圆双折射误差和线性双折射误差与透光轴夹角误差发生同样的变化。
    (2)与偏振分束器的透光轴夹角误差和线性双折射相比,固有双折射误差造成的系统误差相对来说就小得多。
    (3)偏振分束器的透光轴夹角误差和固有双折射误差对整个光纤电流传感系统误差的影响都与传感光纤的线性双折射有着十分显著的关系。随着传感光纤线性双折射误差造成的相位差增大，偏振分束器的透光轴夹角误差引起的系统误差越明显， 而固有圆双折射误差越不明显。
    (4)传感光纤的线性双折射误差是导致光纤电流传感系统测量误差的重要原因。只要有效控制线性双折射误差带来的影响，则偏振分束器的透光轴夹角误差和固有双折射误差就能相对比较好地进行控制。本文通过采用低线性双折射光纤可以有效地降低弯曲等因素带来的线性双折射。
参考文献
[1] 李威.地铁杂散电流腐蚀监测及防护技术[M].徐州:中国矿业大学出版社，2004:1-50.
[2] WARD D A, JLaTExon. Using rogowski coils for transient current measurements[J]. Engineering Science and Education,1993,2(3):105-113.
[3] JOHN D R, DENNIS E D D, START ROBERT S. The  verification of rogowski coil linearity from 200A to greater  than 100 KA using ratio methods[J]. IEEE Instrumentation and Measurement Technology Conference，2002，2(1):687-692.
[4] 李文植.光纤传感器的发展及其应用综述[J].应用技术.科技创业，2005(7):153-154.
[5] 郁道银，谈恒英.工程光学[M].北京:机械工业出版社，1999:340-345.