一种构造压缩感知测量矩阵的新方法

摘  要： 压缩感知理论是近年来针对稀疏信号提出的一种新的信号处理理论。该理论的主要创新之处在于对信号采样和压缩是同时进行的。测量矩阵是实现该创新点的关键步骤之一，其性能直接关系着信号能不能精确重构。利用行列式非零的对角矩阵的正交性，结合正交基线性表示理论，提出了一种新的更简单的测量矩阵的构造方法。通过实验仿真，验证了新矩阵具有较好的性能。
关键词： 压缩感知；测量矩阵；对角阵；正交基线性表示

    压缩感知(compressed sensing）理论是一种对信号中包含的信息进行采样的信号处理理论，旨在突破传统奈奎斯特采样定理关于对采样带宽的要求，并且实现信号采样与压缩同时进行，节省了带宽与存储资源，降低了硬件压力，故一经提出，就受到了信号处理领域研究人员的广泛关注。具体思路是：当信号具有稀疏性或可压缩时，就可以映射到一个低维空间，获取少量的信息采样值，再通过特定重构算法恢复原信号。理论主要研究3个核心问题：信号稀疏表示、测量矩阵和重构算法。其中测量矩阵对信号的重建精度有着直接的影响，测量矩阵性能越好，重建信号与原信号间偏差越小，恢复度越高[1]。因此，研究测量矩阵的构造有很重要的现实意义。
1 压缩感知理论简介
    设x是RN空间的一个N×1维列向量，若该向量中仅包含K个非零值，或者x在N维空间的某个变换基 追下的系数向量中仅有K个非零值，且K<<N，则称x为K-稀疏信号或变换域ψ下的K-稀疏信号。这K个非零值和它们的位置可以表示信号x的全部信息。
    测量矩阵对信号采样与压缩是通过用一个行数M远小于列数N的M×N维测量矩阵Φ与信号x相乘，得到信号在该矩阵下的低维映射y实现的，只要M≥K，即可将信号x中所含的信息完全映射到y中去，同时完成对信号的采样与压缩。测量矩阵不仅要用于信号的采样与压缩，信号的重构过程同样依赖于测量矩阵。CAND 魬S等在参考文献[2]中指出只要测量矩阵满足有限等距约束特性RIP(Restricted Isometry Principle)，即：

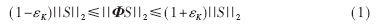
就能够保证准确重建原信号。其中常数 着K称为K阶RIP常数，S为信号的稀疏表示。为了方便实际应用，参考文献[3]给出了测量矩阵满足式(1)的3个等价特征：(1)测量矩阵的列向量组成的子矩阵的最小奇异值应大于一定的常数，即列向量满足一定的线性独立性；(2)测量矩阵的列向量要体现出某种类似噪声的独立随机性；(3)满足稀疏度的解是满足l1范数最小的向量。
    由于M<<N，所以不能直接通过求解测量过程的逆问题得到x。一般信号重建过程可以转化为解l0范数下的最优化问题[4]。            
2 基于正交基线性表示测量矩阵设计及对角阵
    测量矩阵的设计主要是围绕上文中RIP特性的3个等价特征设计的。目前研究的测量矩阵主要分为：(1)随机测量矩阵，主要包括高斯随机矩阵[5]、贝努利矩阵[6]等；(2)确定性测量矩阵，主要包括多项式矩阵[7]等；(3)部分随机测量矩阵，包括部分哈达玛矩阵[6]、托普利兹矩阵[8]、轮换矩阵[6]、广义轮换矩阵[9]等；(4)基于正交基线性表示矩阵，如基于正交基线性表示的哈达玛改进矩阵[10]。

    基于正交基线性表示的哈达玛改进矩阵（以下称为改进的哈达玛矩阵）即是用这种方式构成的测量矩阵。它的正交基选用的是哈达玛矩阵。该方法为了克服哈达玛矩阵对信号维数的限制，提出了可以先产生一个L×L维哈达玛矩阵(L为大于M的最小的2的幂)，然后利用正交基线性表示法产生L×N维矩阵，再从中任取M行作为最终测量矩阵。此时，由于基于正交基线性表示测量矩阵间良好的列相关性是在L×L维哈达玛矩阵上产生的，当M≠2K时，不能保证从M+1列开始之后的任何一列与前M列中的任意M-1个列向量线性无关；另外随机取M行作为最终测量矩阵，一方面给硬件实现造成压力，另一方面将不可避免地造成存储资源的浪费,说明基于正交基线性表示的哈达玛改进矩阵仍未能很好地解决维数所带来的局限性。

3 仿真实验结果
    为了检验新方法构造矩阵的性能及相关理论的正确性，采用Matlab标准图像库中256×256 lena图像进行仿真实验。先用典型的sym8小波生成离散小波变换基对图片进行稀疏处理，再分别用新矩阵、基于正交基线性表示的哈达玛改进矩阵及一些常用测量矩阵对信号进行测量，最后选择基于最小l0范数的正交匹配追踪算法OMP[12](Orthogonal Matching Pursuit)对图片进行重构。在M/N<0.5时，仿真结果如图1所示。

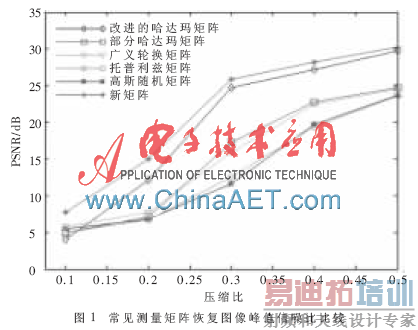
    由仿真图可以看出，基于正交基线性表示的测量矩阵性能要优于其他常用测量矩阵，当压缩比M/N=0.5时，新矩阵的PSNR（峰值信噪比）为30.287 2 dB，改进的哈达玛矩阵为29.742 7 dB，而其他常用矩阵的PSNR均不到24 dB。另外分别比较压缩比为0.1、0.2、0.3、0.4时新矩阵与改进的哈达玛矩阵的PSNR值，可以看出，新矩阵的PSNR值均高于改进的哈达玛矩阵值，尤其是在压缩比为0.2时，差值达到了3 dB。图2给出了在压缩比为0.4时，新矩阵与改进的哈达玛矩阵恢复性能对比，从视觉效果上能够看出新矩阵能以更高的恢复率恢复出原始信号。

    图3给出了在压缩比为0.5时，新矩阵恢复效果图，与原始图已经没有多大差别，进一步验证了新矩阵优良的性能。

    本文旨在研究测量矩阵，在基于正交基线性表示矩阵理论的基础上，结合对角矩阵的行向量和列向量之间良好的正交性，构造矩阵时没有维数限制等性质，提出了一种新的测量矩阵构造方法，即基于对角阵线性表示测量矩阵。该矩阵可以尽最大可能保证列向量间的非相关性。实验选用二维图像进行仿真，并对多种测量矩阵进行实验对比，实验结果验证了新矩阵的可行性与优越性。
参考文献
[1] 吴海佳，张雄伟，陈卫卫.压缩感知新技术专题讲座(二)[J].军事通信技术，2012，33(1)：90-94.
[2] CAND 魬S E，TAO T.Near optimal signal recovery from random projections：universal encoding strategies[J].IEEE Trans. Inform.Theory，2006，52(12)：5406-5425.
[3] DONOHO D.Compressed sensing[J].IEEE Trans.Inform. Theory，2006，52(4)：1289-1306.
[4] CANDS E，WAKIN M.An introduction to compressive  sampling[J].IEEE Signal Processing Magazine，2008(25)：21-30.
[5] DONOHO D，TSAIG Y.Extensions of compressed sensing[J].  Signal Processing，2006，86(3)：533-548.
[6] CAND 魬S E.The restricted isometry property and its implications for compressed sensing[J].C.R.Math.Acad.Sci，2008，346(9-10)：589-592.
[7] DEVORE V.Deterministic constructions of compressed sensing matrices[J].Journal of Complexity，2007，23(4-6)：918-925.
[8] RAUHUT H.Circulant and toeplitz matrices in compressed sensing[J].In Processing SPARS'09，2009，2(13)：1124-1132.
[9] 李浩.用于压缩感知的确定性测量矩阵研究[D].北京：北京交通大学，2011.
[10] 马庆涛.基于压缩感知的信号重构算法研究[D].南京：南京邮电大学，2013.
[11] 李树涛，魏丹.压缩传感综述[J].自动化学报，2009，35(11)：1-7.
[12] TROPP J，GILBERT A C.Signal recovery from partial information via orthogonal matching pursuit[J].IEEE Transactions on Information Theory，2007，53(12)：4655-4666.