无刷直流电机直接转矩控制系统的设计

    摘   要： 针对无刷直流电机直接转矩控制系统速度环节存在的非线性饱和特性，引用新型变结构抗饱和Anti-windup PI控制器，根据控制器的输出是否饱和，对积分状态进行控制。当控制器进入饱和状态，通过调节可以有效地退出饱和；当控制器处于线性区，保证系统渐进稳定。同时利用模糊理论对控制参数进行在线调整，使系统具有更好的实时性。仿真表明，该方法能够有效地抑制饱和现象，减少超调量，使系统具有更好的动静态性能。

    关键词： 无刷直流电机；直接转矩控制；饱和非线性环节；Anti-windup PI控制器；模糊控制

    随着电力电子技术和电机控制理论的发展，无刷直流电机以寿命长、免维护等优点，被广泛应用^[1]。目前一些现代控制理论已应用到其控制领域中， 直接转矩控制^[2-3]就是其中一种。通过检测定子电压电流情况来观测转矩与磁链，得到误差值，然后选择合适的电压矢量来控制逆变器的开关，进而控制电机的运行。过程不涉及内部电流，直接控制电机转矩，动态响应快，对电机参数变化和外部扰动不敏感，具有良好的控制精度^[4]。

    控制系统转速调节一般采用PI控制，控制器的输出就是电机参考转矩值。但由于电机的额定功率和过流过压保护等因素，控制器输出须在一定范围内。故当系统参考输入为一个较大阶跃值或负载突变时，控制器输出出现饱和限制，即被控对象的输入与控制器输出不等，系统闭环响应性能变差，满足不了控制要求，称为windup现象^[5]。参考文献[6]将Anti-windup PI 控制器用在感应电机直接转矩控制中，参考文献[7]用在永磁同步电机控制系统中，都取得了良好的控制效果。本文将其用到无刷直流电机直接转矩控制系统中，速度控制器采用Anti-windup PI控制^[8]，结合了条件积分法和反计算法。前者当控制器饱和时，积分器停止工作，此时控制器相当于P控制；当控制器输出处于线性区时，再加入积分器的作用。后者则是将被控对象的输入与控制器的输出取差值，反馈到积分器的输入端，对积分状态进行控制，从而抑制windup现象。为了实时调整PI参数，引入模糊控制器^[9-10]，比参数固定时有更好的响应特性，提高了系统的鲁棒性及抗干扰能力。仿真结果表明，该方法能够有效地提高直接转矩控制系统的综合控制性能。

1 无刷直流电机的数学模型

    以三相星型二二导通无刷直流电机为例，假设磁路不饱和，三相绕组对称，忽略齿槽效应、涡流和磁滞损耗，分析其数学模型。电机定子绕组电压平衡方程表示为：

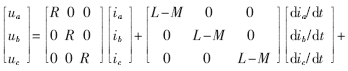
2 无刷直流电机控制系统的设计

2.1 直接转矩控制系统中的windup现象

    直接转矩控制系统的转矩环采用滞环比较器，动态响应速度远高于转速环，故忽略内环转矩动态变化。根据式(3)可得：

2.2 新型Anti-windup PI 控制器设计

    为了克服windup现象的产生，设计了Anti-windup PI 控制器，如图1所示。逻辑开关S在1、2之间切换，分别对应线性区与饱和区，对积分器进行控制。当控制器在线性区时，S与1相连，积分器累加转速误差；当控制器处于饱和区时，S与2相连，把控制器输出与被控对象输入之差反馈到积分器的输入端，消除积分饱和状态。

    控制器积分状态满足：

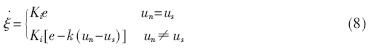
2.3 系统稳定性分析

    由于系统的变结构特性，须分别证明系统不同区域的稳定性。在饱和区，电机参考输入转矩达到限幅值，积分状态衰减到零，系统自动进入线性区，则稳定。而线性区，系统渐进收敛稳定，则证明控制器符合控制要求，全局稳定。

2.3.1 饱和区的稳定条件

    若控制器处于饱和区，即u_n≠u_s，由式(4)可得电机转速误差方程：

    当电机运行状态满足式(15)时，控制器将自动从饱和区退回到线性区。

2.3.2 线性区的稳定条件

    若控制器处于线性区，即u_n=u_s，控制器等效为传统PI控制器。误差方程为：

    当电机运行状态满足式(19)条件时，控制器处于线性区，转速误差收敛为零。

2.4 模糊逻辑对控制器的改进

    利用模糊控制理论对Anti-windup PI控制器中的参数K_p、K_i进行在线修改，将转速误差e及其变化率e_c作为模糊控制器的输入，参数K_p和K_i作为输出，来满足运行中实时变化的e和e_c对系统参数的要求。

    模糊控制器输入变量e及e_c与输出变量K_p及K_i的模糊子集设定为{NB,NM,NS,Z,PS,PM,PB}，并量化在区(-3,3)域内。根据大量模拟仿真实验和前人的电机控制经验，总结出了模糊控制规则集，见表1和表2，最终实现对PI参数的调整。

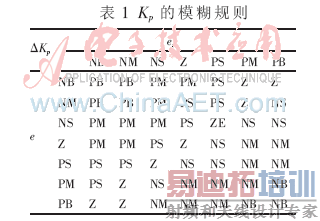
2.5 系统整体设计

    无刷直流电机直接转矩控制系统框图如图2所示。运行后，得到实时的e及e_c，利用模糊规则对控制器参数K_p和K_i实时修改，调整Anti-windup PI控制器的输出,并与实际值比较，得到的控制量与转子位置信号相结合，来选择合适电压矢量，控制逆变器的开关状态，达到控制电机稳定运行的最终目的。

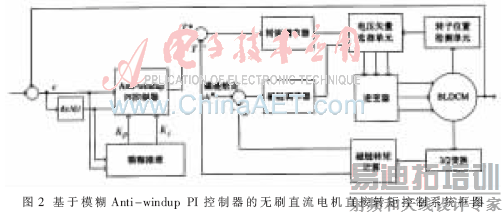
3 仿真及实验结果

    利用Matlab/Simulink建立仿真模型，验证模糊Anti-windup PI 控制器的可行性。仿真框图如图3所示。无刷直流电机参数为:定子绕组电阻R=1 Ω相电感L-M=0.0139 H，阻尼系数B=0.000 2 N·m·s/rad，转动惯量J=0.05 kg·m²，极对数n_p=1，额定转速n=1 200 r/min。模糊Anti-windup PI控制器参数如下：K_p=10，K_i=0.1，k=1。电机空载启动，进入稳态后t=0.2 s外加负载信号T_L=1 N·m，仿真曲线如图4~图5所示。

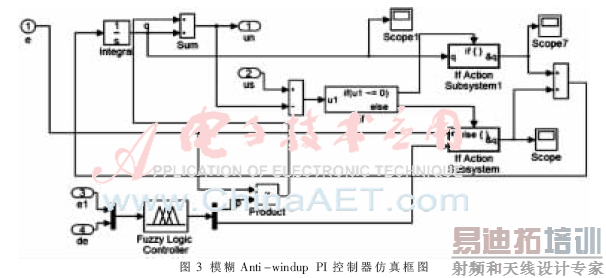
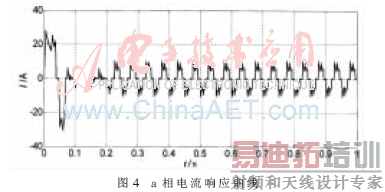
    如图可知，实际波形与理论波形基本保持一致，证明该算法正确可行，系统能在直接转矩控制模型下稳定运行。下面与传统PID控制算法作比较， PID控制器的参数为：K_p=5，K_d=0.001,K_i=0.01。响应曲线对比如图6~图7所示。

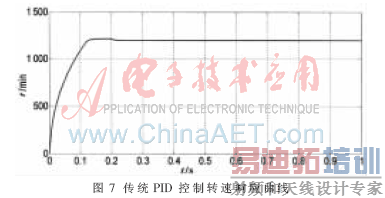
    对比可知，通过模糊Anti-windup PI控制器的调节，有效地抑制了Windup现象，系统更快地进入稳定状态，减小了超调量，具有更好的控制精度。

    针对无刷直流电机直接转矩控制系统转速控制器出现的Windup现象，分析了产生原因，设计了将条件积分法与反计算法相结合的变结构Anti-windup PI控制器，并利用模糊控制规则对控制器参数K_p和K_i进行实时调整，补偿由于e与e_c的变化对参数更高的要求。仿真结果表明，改进后的控制器能有效抑制Windup现象的产生，减小超调量，对干扰不敏感，系统响应快，满足要求的控制精度，具有实际应用价值。

参考文献

[1] 夏长亮. 无刷直流电机控制系统[M]. 北京：科学出版社，2009：1-15.

[2] 夏长亮, 张茂华, 王迎发,等.永磁无刷直流电机直接转矩控制[J]. 中国电机工程学报, 2008,28(6):104-109.

[3] 丁祥. 永磁无刷直流电机直接转矩控制系统的设计研究[D].长沙：湖南大学, 2009.

[4] 李光伟. 无刷直流电机的直接转矩控制研究[D]. 太原：太原科技大学,2009.

[5] 杨明,徐殿国,贵献国.控制系统Anti-windup设计综述[J].电机与控制学报, 2006,10(6):622-626.

[6] 张兴华, 聂晶, 王德明. 感应电机直接转矩控制系统的变结构Anti-windup PI控制器[J].电机与控制学报,2013,17(1):77-81.

[7] 于艳君, 柴凤, 高宏伟,等.基于Anti-windup PI控制器的永磁同步电机控制系统设计[J].电工技术学报,2009,24(4):66-70.

[8] 杜明星, 胡静, 赵刚. 无刷直流电机Anti-windup PI控制系统的研究[J].天津理工大学学报,2008,24(6):86-88.

[9] 王兴贵, 孙宗宇, 王言徐.基于模糊PI控制的永磁同步直线电机矢量控制系统研究[J]. 微电机, 2010,43(5):59-61,69.

[10] 俞钰, 庄健, 于德弘. 模糊抗饱和补偿器的设计及应用[J].西安交通大学学报,2013,47(1):68-73.