不规则区域矩形件排样的一种改进算法

摘  要： 采用遗传算法解决不规则区域的矩形件带排样问题，用有序的带符号整数串作为初始种群个体，改善了初始个体解的质量。提出基于最低水平线的择优插入算法，同时考虑不规则区域的左右两端区域，选取最适合的零件进行填充，使零件排放紧凑，提高了材料的利用率。
关键词： 遗传算法；排样；最低水平线

　矩形件带排样问题(RSPP)是在不规则板材上布置多个大小不同的矩形零件，并满足以下约束条件：(1)零件排放在板材内部；(2)各零件之间互不重叠；(3)满足一定的工艺要求。其优化目标是寻求一个零件布局方案，使得浪费的板材面积最小，亦材料的利用率最大。排样问题对造船、服装、模具等材料加工行业有重要意义，材料利用率的提高可直接降低材料浪费，提高经济效益，也符合当今创建节约型社会的需求。
与参考文献[1]中的矩形件带排样相比，不规则区域的排样增加了对板材两端空洞的利用，实际上增加了两端空洞排样时的搜索，所以不规则区域的排样问题在几何计算方面的复杂度较高。在满足约束条件的情况下，矩形排样的最低最左原则或最低水平线原则在不规则区域排样的情况下已不能满足需要，最低最左等传统放置方法将导致较大的空白区域无法利用。
　最大限度地节约材料、提高材料利用率是生产中提高效益的一个重要手段。由于排样问题的广泛存在，如板金下料、报刊排版、服装裁剪等，都需要在可接受的时间里得到最优或近似解。
参考文献[1-3]中提到的利用遗传算法求解的矩形件排样问题，均采用遗传算法和改进的最低水平算法进行计算，利用此方式对不规则区域排样，得到的排样图出现明显的空洞。本文提出一种新方法，通过对板材两端空洞的利用，提高板材的利用率。
1 算法描述
1.1 本文改进遗传算法流程图
　本文采用十进制的编码方式对每一个矩形零件进行编码，将每一个矩形编号，i=1，2，…，n，零件编号构成一个整数串P={p1，p2，…，pn}，1≤Pi≤n，表示了一种排样图(即一个个体)。
初始种群的好坏对遗传算法的收敛速度和求解质量有较大的影响。本文在初始种群时，分析了矩形零件的数据特点，采用经验选择与随机生成相结合的初始方法，大矩形件排放完后再排小矩形，材料利用率不会太低。
　算法开始，首先将零件根据面积降序排列，面积相等时根据长度降序排列，产生一个有序整数串，再随机产生m个个体，构成初始种群。利用每个个体排列所得排样图的高度计算得出该个体的适应度值，进行选择、交叉和变异之后，再判断是否达到了计算次数或得到了满意的结果。如果没有达到，则返回重新计算每个个体的适应度值；否则，算法就结束。算法流程如图1所示。

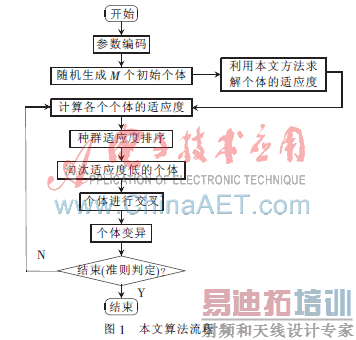
1.2 基于最低水平线的算法
　由遗传算法产生一个个体编码后，只有将此个体对应的零件固定序列快速地求出其对应的排样图，得到所需要占据的板材高度，才能计算其适应度值，从而对该个体进行评价。本文在文献[1]方法的基础上提出一种基于最低水平线的择优插入算法，对给定的零件固定序列进行优化排样，降低排样高度，使零件排放紧凑，提高材料利用率。
　针对不规则区域的排样时，利用此算法的搜索策略有两种方案：一种是向后搜索到一个可以放下的零件时马上停止搜索；另一种是向后搜索所有可以放下的零件，再从中选择一个宽度最大的，使空间得到较为有效的利用。本文采用第二种方案。
　当搜索到最优零件后，参考文献[2]中采用的是“互换”两个零件位置的方式。如果最优零件位置比较靠后，且最优零件小于当前排放零件面积，则当前面积较大的零件就会调整到后面的位置。如此多次搜索、互换零件位置可能造成在排样的前期将较小尺寸的零件全部利用掉，后期剩下的都是大尺寸零件；而较大尺寸的零件对排样高度的影响较大，这样可能会出现即使前期得到的排样图零件紧凑、空洞较小，但后期总体排样高度骤增的情况，导致得不到高质量的排样图。
　此时采用文中的插入策略，将此时搜索到的最优零件直接插入到当前的零件之前。
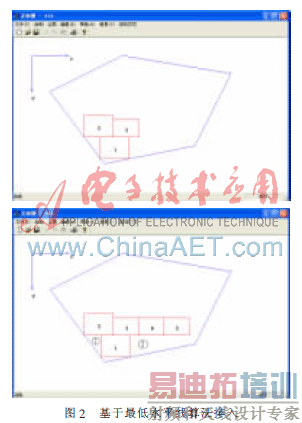
在零件排放过程中会出现多段最高轮廓线，如图2所示，最低水平线为当前所有轮廓线中最低的一段。如有数段，选择最左的一段，其位置和长度在整个排样的过程中不断变化，如图2所示。本文提出了一种基于最低水平线搜索算法，步骤如下：

　(1)设置初始最高轮廓线为板材的最下面的边(板材在竖直方向无限高)。
　(2)当前要排入的零件为Pi，当前最低水平线为Llowest，比较是否大于或等于Pi。若大于，则将Pi在Llowest上排放，更新最高轮廓线；否则，在序列中从Pi位置开始向后搜索一个可以排放的零件，同时互换这两个零件的位置；如果没有搜索到，则将Llowest提升至与其相邻且高度较低的一段平齐，更新最高轮廓线。
重复(2)，直至所有零件排放完毕。
　其中水平线属性为：
　class line{double left；//水平线左端点的横坐标
　double wide；//水平线的宽度
　double high；}；//左端点的纵坐标
　基于最低水平线，对于不规则区域的矩形件排样，采用扫描的方式找出不规则区域中最低且能排入此矩形件的水平线。按照最低水平线得到图2。
如图2，可以明显看出，在①中可以插入后面的更小的矩形件，或者将4或5塞入其中，可以减少总排样图的高度。在②中可以将2插入其中，这样也完全可以增加不规则区域的利用，减少总排样图的高度。
1.3 本文改进算法
　当每排完一个矩形件，依照上述算法就要更新最低水平线，此时只适合针对矩形板材的排样，不规则区域的排样会出现上述大规模的空间浪费。
　本文提出基于最低水平线的改进算法：在更新水平线的同时，需判断水平线首尾元素的宽度是否为0，如果不为0，则要在首元素添加头元素：先取得首元素指针head，过点(head->left，head->high)与不规则区域相交，取下面的一点pt。新增line对象，line(pt.x，0，pt.y)，将pt添加到首元素。判断水平线尾元素与判断首元素类似。
　针对最低水平线搜索算法的改进算法的步骤如下：
　(1)判断底边是否水平，若水平且能排入当前的矩形件，则排入零件；否则向上扫描直至找到能排入的水平线段，排入零件。
　(2)当前要排入的零件Pi，当前水平线为Llowest，判断Llowest->wide与Pi.wide的关系。若Llowest->wide大于或等于Pi.wide，则转入(3)，否则转入(4)。
　(3)判断排入到该水平线上的零件是否超出不规则边界。如果此时的零件没有超出不规则区域，则排入此零件，且更新水平线。否则，此时的零件超出了不规则区域，如果超出了右侧边界，则不能排入此零件，同时向后搜索能够排入的零件，如果搜索不到则直接更新水平线。如果超出了左边界，则向右移动此零件直至不超出边界，移动距离为s，移动之后的零件Pi仍大于Llowest-s，则排入此零件。如果移动之后的零件Pi小于Llowest-s，则需向后搜索能够排入且不超出边界的零件，如果搜索不到则直接更新水平线。搜索到了则将该零件排入到当前水平线上，同时更新水平线。回到(2)。
　(4)判断此时的Llowest是否是最低水平线段的首元素或尾元素。如果不是，则在序列中从Pi位置开始向后搜索一个可以排放的零件，同时将这个零件插入到Pi之前的位置；如果没有搜索到，则将Llowest提升至与其相邻且高度较低的一段平齐，更新水平线。如果是，则转入(5)。
　(5)如果Llowest是最低水平线段的首元素，则获取此段水平线的下一个元素next，求得点(next->left，next->high)到不规则区域左侧边的距离为d，此时且有零件序列中宽度最小元素Plowest。如果d小于Plowest.wide，则更新next，将Llowest->left赋给next->left，同时next的宽度增加d，同时删除首元素。如果Pi.wide大于或等于d，则在序列中从Pi位置开始向后搜索一个可以排放的wide最大的零件，同时将此时找到的元素插入到当前Pi的前面；如果没有搜索到，则同样更新next，同时删除首元素。否则Pi.wide小于d，则此时可以将此零件排入首元素，从下往上扫描，直到找到大于或等于Pi.wide的线段为止，之后更新水平线。如果是最低水平线的尾元素，此时与首元素的处理类似。
重复(2)，直至所有零件排放完毕。
　由图3可以看出，经过本文改进算法的排入图，零件总排样高度有了明显降低，整个优化排样过程都紧凑地排放零件，使不规则区域的“空洞”区域得到了有效利用，提高了材料利用率。有效地将最低水平线算法在不规则区域排样领域应用。

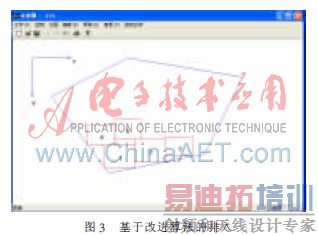
2 遗传算法的过程
2.1 遗传算子
　(1)交叉算子。将父辈种群中的个体随机两两配对，进行单点交叉操作，产生m个新个体构成种群。设随机选定的2个进行交叉的个体分别为P={p1，p2，…，pn}和Q={q1，q2，…，qn}。单点交叉是在1∪n范围内随机生成一个交叉位t，从P中将位于t之前的元素拷贝至子代个体I1中作为前面的元素，P中未拷贝元素按Q中出现的先后顺序拷贝至I2；同样的方法可以产生另一新个体I2。
　(2)变异算子。对交叉操作产生的子代个体，利用两种变异算子进行变异：①旋转变异。在1∪n范围内随机产生一个旋转位，以概率Pm1对子代个体中位于其后的矩形零件进行旋转；②颠倒变异。在1∪n范围内随机产生2个变异位，以概率Pm2对子代个体中两个变异位之间的所有零件颠倒顺序。
当零件个数较少时，颠倒变异可以提高算法的局部搜索能力。而零件个数较多时，解码过程中动态调整动作相应增多，则在遗传过程中的顺序调整意义不大。所以解决大规模矩形件排样问题时，只考虑旋转变异。
　(3)选择算子。对变异后的m个子代个体依次求解其适应度，并分别与其父辈个体的适应度进行比较，若大于其父辈个体的适应度值，则接收此子代个体，替换其父辈个体作为下一代的父辈个体；否则，不接收此子代个体，其父辈个体直接进化，作为下一代的父辈个体。
2.2 适应度函数
　遗传算法对一个解的好坏用适应度函数进行评价，适应度越大，解的质量越好。本文采用参考文献[2]中的适应度函数f(p)=Area/Area0，其中Area是矩形零件的总面积，Area0是排样图最大高度以下的面积，适应度值最大为1。
2.3 终止准则
　重复执行，直到最好解的适应度达到要求或满足预定的进化代数，停止计算，输出最优解。
3 实验计算
　依据表1所给数据，在改进遗传算法的基础上做了一组实验。

　采用遗传算法和最低水平线进行计算，设定板材的端点顺时针为(300，50)(100，150)(250，350)(500，300)(600，100)，得出如图4所示的排样图。

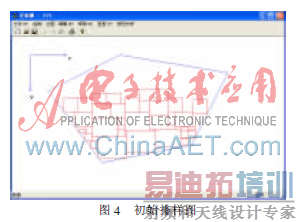
　此时排样图的最高轮廓线为(383.5，80，146)，其中高度为146。上述排样图的适应度为0.723。
采用遗传算法进行计算，设定种群规模m=20。迭代100次计算20次，取其平均适应度作为评价参数，得到如图5所示的排样图。

　此时排样图的最高轮廓线为(516.25，40，157)，其中高度为157。排样图的适应度为：0.784。
经过遗传算法的迭代求解，排样图的整体高度已经有了很大的改进。
对于求解不规则区域的排样，本文在最低水平线的基础上提出了改进，并利用遗传算法，使不规则区域的面积利用率更为有效。
　在研究不规则区域排样的问题中，需要考虑的是整体排样图的高度。利用所给的布局函数和目标函数值，确定整体排样图的高度。本文提出的搜索算法中的前后端搜索方式还有待改进。不规则区域的布局可以使用本文算法。由于变异算子、交叉算子等数值对遗传算法的影响，本文在适应度方面还有待改进，可以提高效率。
参考文献
[1] 赵新芳，崔耀东，杨莹，等.矩形件带排样的一种遗传算法[J].计算机辅助设计与图形学学报，2008(4).
[2] 龚志辉，黄星梅.二维矩形件优化排样算法的改进研究[J].湖南大学学报(自然科学版)，2003，30(3)：47-49.
[3] HOPPER E， Turton B C H. A review of the application of metaheuristic algorithms to 2D strip packing problems [J]. Artificial Intelligence Review， 2001，16(4)： 257-300.
[4] 贾志欣，殷国富，罗阳.二维不规则零件排放问题的遗传算法求解[J].计算机辅助设计与图形学学报，2002，14(5)：467-470.
[5] 龚志辉.基于遗传算法的矩形件优化排样系统研究 [D].长沙：湖南大学，2003.
[6] 黄红兵.矩形毛坯优化排样算法的改进[J].机械工程师，2004(11)：12-14.
[7] HOPPER E， Turton B C H. An empirical investigation of metaheuristic and heuristic algorithms for a 2D packing problem[J]. European Journal of Operational Research， 2001， 128(1)：34-57.
[8] Zhang D， Kang Y， Deng A. A new heuristic recursive algorithm for the strip rectangular packing problem[J]. Computers & Operations Research， 2006， 33(8)：2209-2217.
[9] Zhang D， Liu Y， Chen S， et al. A meta-heuristic algorithm for the strip rectangular packing problem [M].Lecture Notes in Computer Science. Heidelberg： Springer， 2005，612： 1235-1241.