一种斜拉桥索力检测的基频混合识别方法

摘  要： 介绍了斜拉桥索力检测力学计算模型构建、加速度时程FFT频谱分解、超低基频的自功率谱实测法、倒频谱原理以及自功率谱与倒频谱混合识别法，并结合采用VB和MATLAB程序开发的软件系统进行索力检测应用试验与分析比较。
关键词： 索力检测；计算模型；基频；混合识别

　斜拉桥拉索在桥梁动载和风雨作用下引起的随机性振动，会造成拉索的疲劳破坏，降低拉索疲劳寿命，从而严重影响桥梁的安全运行。目前，在索力监测与状态评估的测量中通常采用基于环境振动的频率方法，关键在于准确识别不同条件下斜拉桥拉索的基频。
    本文以大跨度多索斜拉桥为研究对象，通过建立索力检测力学计算模型，基于频谱分析原理，提出了一种自功率谱与倒频谱相结合的基频混合识别方法，并在宁波招宝山大桥上进行了基频识别试验研究。
1 斜拉桥索力力学计算模型
1.1 斜拉索自由振动方程及特征值求解
    不计斜拉索的轴向振动，由牛顿定律并考虑索的垂度及抗弯刚度，可以得出斜拉索自由振动方程[1]如式(1)所示。
 
其中，H、h分别为X方向静、动张拉力，在整个索长L范围内为常数。用中心差分法求解，将索均分为n+1段，每段长度a=L/(n+1)。将式(2)中微分项化为各节点位移形式。
 
    则由式(3)可以求得n对共轭特征值p1，再由式(1)求出各阶模态无阻尼自振频率。
1.2 确定索力与自振频率的关系
    由式(2)和式(3)可知，特征分析得到的自振频率与拉索张力是对应的，即某一张力值，可以计算出拉索对应的各阶自振频率。使用频谱分析及参数识别技术，由环境振动测试得到的振动加速度信息，可识别出拉索振动频率。根据拉索振动频率，由标准弦振动频率方程[3]可得出张力：
    
式中，T为拉索的轴向张力，fn为拉索的n阶振动频率，n为拉索的振动频率阶数。
    从式(4)可见，对同根缆索，张力一定时，其各阶自振频率的频谱是等间距的，且间距等于它的一阶自振频率f1。对于实际拉索，需要考虑索的刚度、垂度和两端固定方式、阻尼器的介入影响。研究表明[4]，对于60 m以上的长索，用式(4)即能获得工程上满意的结果。在式(4)中，令n=1，则有：
  
    式(5)为拉索基频与索力的关系式。可见，对于某一根确定的拉索，ρ、l都是已知值，如果能精确测定f1，便可求得拉索的张力。此时，已经将求拉索索力的问题转化为求拉索在随机振动源激励下振动的基频问题。

2 随机振动频率法测索力
2.1 加速度时程FFT频谱分解
    随机振动频率法是根据式(5)所示的基频与拉索索力的关系，通过对传感器拾取的拉索随机振动信号的自功率谱分析，得到拉索振动的基频后，计算拉索索力。宁波招宝山大桥16号斜拉索的参数如表1所示，在拉索长18%的位置上安装了压电式加速度传感器。试验中，数据采样频率为1 000 Hz，滤波截止频率为300 Hz，并以面内测试数据为分析对象，在环境激励下测得的自振信号如图1所示。

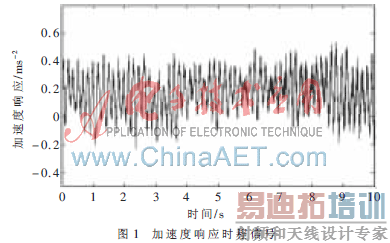
    图2为拉索振动响应的主要组成部分3、4阶频率成分。由振动学理论可知，拉索第一振型最大振幅位置在斜拉索的中央，越靠近端部振幅越小，第二振型最大振幅在l/6、3l/6、5l/6等位置。即在斜拉索的端部，距离第一振型最大振幅位置最远，距离较高阶振型的最大振幅位置较近。

2.2 超低基频的自功率谱实测法
    一般结构在环境振动的激励下，总是依自己各个自振频率作多个模态的复合振动。其中包含的低频振动分量，特别是一频振动分量最多，振幅也较大。但由于拉索振动的特殊性，以及测量索力时的工作状态，造成其低阶自振的分量较少，高阶自振的分量较多。反映在振动测量结果上，其频谱图中，较高自振频率的谱峰较高，较低自振频率的谱峰很小，有时甚至分辨不清。
    若低阶自振频率难以测量，就不能用式(4)、式(5)计算索力，但是可以通过频谱图上各个频谱相应的自振频率阶数求解。当n=1时，由式(5)得：
    
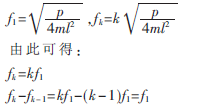
    可见，无弯曲刚度拉索的各阶自振频率的频谱是大致等间距的，其间距等于它的一阶自振频率(基频)。即无弯曲刚度拉索各阶自振频率之比为1:2:3:4，它体现了无弯曲刚度拉索的振动特征。
    利用相邻两谐振峰之间的频率，先初略估算出基频f1′，同一频谱图中的f1′的相对误差一般不可能超过10%，以它的平均值作为基频f1从理论上讲是可行的，但实测时会带来较大的误差，影响测试精度。
    因此，从频谱图中选取一处幅值较大，较靠近基频的谐振峰，若它是拉索的次谐振频率形成的峰，算出基频f1=fn/n，然后频谱图中的前后峰值的比值应非常接近于整数，fn前的峰值对应算出的整数为n-1、n-2，fn后的峰值对应的整数为n+1、n+2。若不满足这些要求，说明假设的不是拉索的次谐振频率形成的峰，可用加1或减1再试算一次，直至找到基频f1。
    由于环境振动的随机性大，其结果变异性也大，采用自功率谱与倒频谱混合识别法能保证计算结果的准确性。
3 自功率谱与倒频谱混合识别法
3.1 倒频谱原理
    倒频谱的表达式为[5]：
    
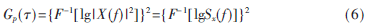
式中，X(f)与Sx(f)分别为信号x(t)的傅里叶变换与自功率谱密度函数。
    从式（6）可见，倒频谱是对信号y(t)的自功率谱Sy(f)的对数值进行逆傅里叶变换的结果。它可将复杂的自功率谱先化为一系列卷积或乘积的形式，再通过取对数转化成简单和的形式，这样便于识别信号的组成分量，可更好地提取其中有用的信号成分。信号经倒频谱变换后，滤出传递函数的分量，再用傅里叶正变换等运算，得到输入信号的幅值。该过程能将响应信号中的输入效应和传递途径的效应分离开来，使分析结果受传输途径的影响很小。例如，要了解功率谱信号Sx(f)，可对其Cx(s)进行傅里叶正变换，得到lnSx(f)，再作对数运算，求得信号功率谱Sx(f)。
    利用倒频谱这一特点，可将原来谱图上成族的边频带谱线简化为单根谱线，则能识别出复杂频谱图上的周期结构，分离和提取出密集泛频信号中的周期成分，这对于具有周期成分及多成分边频等复杂信号的识别尤为有效。鉴于振动的索的功率谱上的峰值具有明显的周期性特征，因此，把自功率谱与倒频谱分析结合起来，能更好地识别斜拉索的频率。
3.2 斜拉索基频混合识别
    用高灵敏的压电加速度计测量拉索的振动信号，振动信号经电荷放大器放大和数字滤波处理，数据采样频率为1 000 Hz，经FFT变换，得到自功率频谱函数。
    如果测得的拉索振动信号在低、中频范围内有好的信噪比，通过FFT，则能获得频段清晰的梳状自功率频谱图。但由于索力检测感兴趣的频带一般在0.5 Hz～50 Hz，而拉索的振动信号是由多谐振动信号组成的复合振动信号，当针对感兴趣频带设定合适的采样周期时，其高频成分容易使FFT发生混频现象，致使在实测中得出的自功率谱图常常是不规则的。因此可在数字滤波器的输入端设置一截止频率为300 Hz的滤波电路，从而有效地抑制高频混叠现象。
    经过滤波及FFT变换后对所得到的自功率谱函数分别利用超低频自功率谱法以及倒频谱法计算基频及识别。在宁波招宝山大桥实际索力测试中，运用该方法，系统能够自动识别拉索基频，结果准确可靠。
3.3 基频识别流程
    以VB应用程序作为系统主控，进行流程图显示、相关参数设置、实时数据采集等；以Matlab作为后台应用程序进行检测系统分析、检测系统设计、大量的数值分析和曲线绘制等。斜拉索基频检测流程图如图3所示。

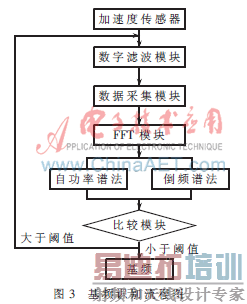
4 工程应用
4.1 应用实例
    宁波招宝山大桥总长567 m，斜拉索共计102根，直径0.15 m，桥面宽29.5 m，通航净高32 m。试验中以上游C16～C20以及下游C16′～C20′号索为检测对象。
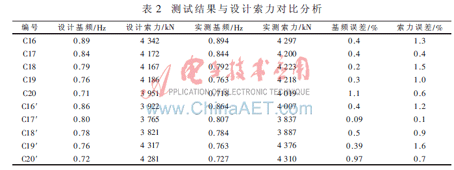
4.2 测试结果
    上游C16～C20以及下游C16′～C20′号索测量的基频及索力如表2所示。结果表明，测试结果与实际索力高度吻合，其误差远小于5%。

    本文基于频谱分析原理，提出一种自功率谱与倒频谱相结合的基频混合识别法，以及相关的理论和算法，并利用该方法对宁波招宝山大桥斜拉索索力进行监测试验。结果表明，该方法检测精度高，在工程应用中具有推广价值。
参考文献
[1] 刘志军，党志杰.振动法测定缆索张力的研究[J].桥梁建设，2002，32(2)：22-25.
[2] 陈歆贤.桥梁工程索力的测试方法研究[J].福建建筑，2003，36(4)：15-18.
[3] 陈水生，孙炳楠.斜拉桥拉索模态耦合非线性共振响应特性[J].工程力学，2003，20(2)：7-9.
[4] 陈水生，秦鸣，陈勇.大跨度斜拉桥拉索的振动及控制现场试验[J].长安大学学报，2003，23(2)：19-21.
[5] 程珩，程明璜.倒频谱在齿轮故障诊断中的应用[J].太原理工大学学报，2003，34(6)：661-663.
[6] 樊金荣，黎洪生.浅谈VB与Matlab相结合的三种方法[J].微型电脑应用，2003，19(4)：60-62.