非均匀采样信号的滑动滤波方法

摘  要： 针对实际采样过程中出现的采样非均匀性，提出了基于连续傅里叶变换的非均匀采样信号频谱分析方法和非均匀采样信号的滑动滤波方法。将非均匀采样信号描述为不均匀采样时刻冲激函数代数和的形式，利用连续傅里叶变换得到非均匀采样信号的频谱特性，根据不同采样间隔，得到非均匀采样信号的滑动滤波方法。通过MATLAB仿真软件验证了这种非均匀采样信号分析与处理方法的正确性，将这一研究成果应用到机械抖动激光陀螺输出信号处理中，与常规的平均滤波方法相比，激光陀螺的零偏误差减少了10.1%。
 关键词： 非均匀采样； 滑动滤波； 频谱分析； 傅里叶分析

    目前的数字信号处理几乎都是基于均匀采样来描述信号特征，但在许多实际的数据采集系统中,如激光陀螺捷联惯导系统和多路A/D转换电路中，由于采用整周期采样技术或由于时钟脉冲的不稳定性，造成采样时间间隔是非均匀的。在进行谱分析和数字信号处理时，由于引入了时间归一化过程，采样序列的自变量以整数形式给出，没有任何关于非均匀采样时间间隔的信息，这必然导致频谱分析及信号处理结果都存在误差。同时非均匀采样在整个频带范围内都会产生频谱噪声，甚至可以淹没幅度小的信号频谱，使得检测和处理幅度小的信号较为困难。
    国内外学者对非均匀采样信号的处理方法进行了深入的研究，JENQ Y. C.最早用分析的方法研究了非均匀理想抽取正弦信号的频谱问题[1]，其基本思路是将非均匀采样序列用M个均匀的采样序列组合来表示,并建立非均匀采样序列的离散频谱和原来信号模拟频谱之间的关系。在此基础上参考文献[2]讨论了非均匀采样信号的频谱分析方法，从数学期望的角度证明了该方法的正确性。参考文献[3-5]深入研究了非均匀采样信号数字谱，并给出了非均匀采样周期信号的数字谱表达式。在滑动滤波方面，PELED A讨论了滑动滤波在信号处理中的应用及其可行性[6]。虽然这些卓有成效的研究成果大大促进了非均匀采样信号分析理论的发展，但只适用于多个周期采样的叠加情况，同时对非均匀采样信号的滤波问题还有待研究。
     本文深入研究了非均匀采样信号的数字谱，得到了非均匀采样信号数字谱计算的表达形式，提出了非均匀采样信号的滑动滤波方法。应用非均匀采样信号的谱分析方法和滑动滤波方法，分析了激光陀螺输出信号的谱特性，并有效地减少了激光陀螺的零偏信号。

式(2)得到的频谱在频域是连续的，不适宜在计算机处理，为此需要对频域离散化。
     在时域上把非均匀采样的N点按周期T0进行周期延拓,即把该区间内的波形平移nT0后叠加到原波形处形成周期波形。由于周期延拓中的搬移可以通过与 啄(t-nT0)的卷积来实现，因此周期延拓后的波形在数学上可以表示为原始波形与冲激串序列的卷积，其结果具有离散谱。周期延拓信号为：
 
    这样，经过时域抽样、截断和周期延拓后，在N个非均匀时间抽样值与N个频率抽样值之间建立了联系，而且经过处理后的新信号的傅里叶变换Xs(k/T0)可以看成是原信号傅里叶变换的近似。
2 非均匀采样信号的滑动滤波方法
    对于等间隔时间 驻T的采样信号序列,滑动平均滤波法就是连续取N次采样值进行算术平均，其数学表达式是:

    非均匀采样信号滑动滤波器的频谱计算如图1所示。从图1可以看到滑动平均滤波相当于一个低通滤波器，衰减了较高频率的信号，对数据起到了平滑作用。图中实线为滑动窗口宽度，虚线为的振幅函数曲线，窗口越宽通带越窄。

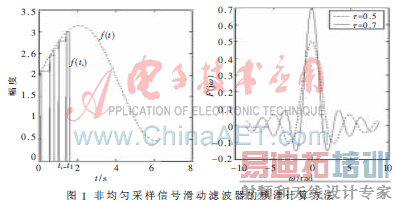
     利用这个特点，通过合理设置窗口宽度，可以在抑制噪声的同时尽可能保存信号，从而达到提高信噪比的目的。从另一个角度来看，滑动窗口内的数据在求平均时，由于噪声是随机的，不会积累，而信号会积累，所以信号得以突显出来。
3 仿真验证
     MATLAB作为数值分析和信号处理软件，已广泛应用于科学研究和工程实践中解决各种实际问题。本文利用MATLAB数据处理功能对非均匀采样信号的数字谱进行计算分析，并且验证滑动滤波方法的有效性。
 

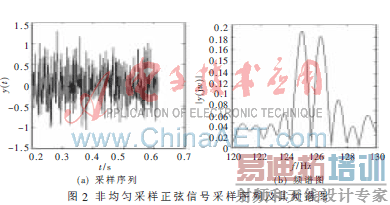
    因此,基于非均匀采样的频谱算法在处理相同数据长度的采样数据时，可以提高频谱的频率分辨率。
    利用式(7)对混有噪声的信号(式(9))进行16点滑动滤波处理，其误差均值和方差为0.001 3、 0.011 1，而采用常规的平均滤波法对非均匀采样信号进行滤波处理，误差均值和方差分别为0.002 8、0.012 5，从而验证了本文提出的滑动滤波方法的有效性。
4 非均匀采样信号滑动滤波方法在工程实践中的应用
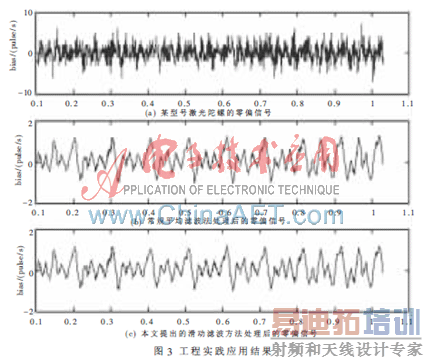
    激光陀螺是一种以量化脉冲的形式输出角增量的数字传感器，它的读出电路输出脉冲个数，每个脉冲对应着采样时间内的角增量。而当激光陀螺输出量化脉冲的整数倍时,测量信号的采样间隔不是固定不变的，这就造成了采样时间的非均匀性，因此激光陀螺的输出信号是非均匀时间采样下的正弦信号。激光陀螺的零偏误差是衡量其性能的主要技术指标，它的大小直接关系到捷联惯导系统的稳定性和导航精度[7，8]。
    图3(a)为某型号激光陀螺整周期采样的零漂信号，其均值和标准差分别为0.091 3 pulse/s和4.336 4 pulse/s,该零偏信号经过常规的平均滤波和本文提出的非均匀滑动滤波方法处理后,均值分别是0.107 5 pulse/s、0.100 7 pulse/s,速率标准差分别是0.245 3 pulse/s、0.220 4 pulse/s。从实验的结果可以看出，经过非均匀滑动滤波器后激光陀螺零偏的标准差得到有效的减少，误差标准差较常规方法减少了10%。从经过滑动滤波处理后的数据可以准确估算出激光陀螺的随机游走系数为0.0064°/。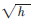

    针对数字信号处理中的非均匀采样问题，本文提出了非均匀采样信号的频谱分析和滑动滤波方法。对非均匀采样信号的数字谱进行计算分析，得出传统的快速傅里叶变换要想提高频率分辨率就要增加采样点数，但这样就增加了数据冗余性和计算的复杂性，而基于非均匀采样的频谱算法在处理相同数据长度的采样数据时，可以提高频谱的频率分辨率。非均匀采样滑动滤波方法解决了采样间隔不均匀的问题，衰减了高频率的信号，对(上接第77页)
数据起到了平滑的作用。把这一研究成果应用到机械抖动激光陀螺正弦抖动信号的分析和滤波处理中，激光陀螺的零偏误差得到了有效的降低。
参考文献
[1]  JENQ Y C. Digital spectra of non-uniformly samples signals: Fundamentals and high-speed waveform digitizers[J]. IEEE Trans. Instrum. Meas.,1988,37(2):245-251.
[2] TARCZYNSKI A, VALIMAKI V,CAIN G D. FIR filtering of non-uniformly sampled signals [J]. IEEE Inter. Con. On Assp, 1997(3):2237-2240.
[3] OUAHABI A,DEPOLLIER C, SIMON L,et al. Spectrum estimation from randomly sampled velocity data[J]. IEEE Transactions on Instrument and Measurement, 1998,47(4):1005-1012.
[4]  JENQ Y C. Digital-to-Analog(D/A) converters with nonuniformly sampled signals[J]. IEEE Transactions on Instrumentation and Measurement, 1996,45(1):56-59.
[5] LIN Y P, VAIDYANATHAN P P. Periodically non-uniform sampling of band pass signals [J]. IEEE  Trans. Circuits and Systems. 1998(3):340-351.
[6] PELED A, LIU B. Digital signal processing,theory,design, and implementation. New York: John Wiley,1976:20-27.
[7]  高玉凯,邓正隆.消除机械抖动激光陀螺闭锁误差的方法[J].中国激光，2007,34(3)：354-358.
[8]  高玉凯,邓正隆.改善机抖温度特性提高激光陀螺检测精度的方法研究[J].系统仿真学报,2007，19(14)：3297-
    3330.