基于神经网络预测器的传感器数据证实技术研究

　　摘  要： 提出了基于神经网络预测器的传感器数据证实技术。首先利用神经网络对传感器输出的时间序列建立预测模型，然后利用该模型预测出传感器输出值，并用该值与传感器实际输出值之差判断传感器实际输出的可靠性和有效性，进而减小传感器“软故障”和不同环境噪声对传感器输出数据的影响。同时，为了实现在线应用，采用了遗传算法对神经网络的优化技术。

　　关键词： 传感器数据证实  神经网络  遗传算法

 　　对于高速、大容量、高性能的复杂装置和设备，在运行中如果出现故障往往会产生巨大的、甚至是灾难性的后果。对这些装置和设备运行状态的监测与诊断是解决其可靠性、安全性的关键途径之一。作为测量控制系统中诸参量的关键部件，传感器被广泛地应用到这些装置和设备中。可以说，传感器技术是现代测试和控制技术的灵魂，传感器输出信号的质量关系到整个系统性能的好坏程度。事实上，传感器是测试控制系统比较容易损坏的部件，因此系统应该具备对传感器故障的容错能力。目前，传感器故障诊断较多地采用冗余方法和神经网络识别方法。这些方法都需要利用传感器的输出信号，且研究较多的是判别传感器的“硬故障”(即突然发生的损坏或完全失效)。对于传感器的“软故障”(如偏置、漂移或标定系数的偏移等)的研究工作，开展得还不多，存在很多问题急需解决。为此，本文提出一种基于神经网络预测器的传感器数据证实技术。

1 神经网络预测器原理

　　神经网络具有很强的非线性映射能力。一个三层的前馈神经网络具有映射任意函数关系的能力，且不需要对所分析的时间序列作任何假设。因此神经网络非常适用于时间序列预测，且神经网络预测模型具有良好的适应性、自学习和抗干扰能力强等特点。在建立神经网络预测模型进行时序预测的过程中，如何选择、确定预测网络的拓扑结构是非常重要的，这将直接影响预测的精度。要提高神经网络预测模型的预测精度，可以采取以下途径:

　　增加网络模型的训练样本数。这样可以使得神经网络得到更好的训练和学习，从而更准确地学习和掌握时间序列内在的变化、发展规律，提高预测质量;

    适当增加神经网络的输入层节点数。因为如果神经网络的输入层节点数过少，将使神经网络无法达到对时间序列的良好拟合，从而降低神经网络的预测精度。但并非神经网络的输入层节点数越多越好。相反，如果输入层节点数过多，则将减慢预测网络的训练和收敛速度，并使网络模型过于复杂，导致网络预测能力的恶化。

    随着网络规模的扩大以及训练样本复杂度的增加，BP算法存在收敛速度慢、振荡，特别是受到局部最优的困扰，很难保证得到全局最优解。为了能在线应用，因此对网络进行优化是必要的。本文采用遗传算法(GA)来优化网络的权值以提高网络训练速度，达到在线应用的需要。

　　GA的计算过程为:

    选择编码方式

              产生初始群体

              计算初始群体的适应性值

              如果不满足中止条件{

                                          选择(selection)

                                          交换(crossover)

                                          变异(mutation)

                                          计算新一代群体的适应性值

                                                 }

　　遗传算法的实现涉及5个主要因素:参数的编码、初始群体的设定、评估函数即适应度函数的设计、遗传操作(选择、交叉、变异)的设计和算法控制参数的设定。所有这些因素的实现都是基于模式定理和积木块假设的。本文初始群体数目为40～100，算法控制参数为神经网络的权值，参数采用二进制编码，适应度函数为神经网络的能量函数。

采用GA算法和梯度法的结合即混合优化方法，具体步骤如下:   

　　(1)确定适应度函数。对BP网络，定义其能量函数为:

　　式中，Y_ki为第k个训练样本第i个输入节点的实际输出，为第k个训练样本第i个输入节点的期望输出。

　　神经网络的优化过程即是调整权矩阵W和阈值矩阵θ使得E最小的过程。因此，优化目标函数为:

　　混合优化算法的目标是要找到一权矩阵W0和阈值矩阵θ₀，使得式(2)取最小值。故定义评价神经网络优劣的适应度函数为:

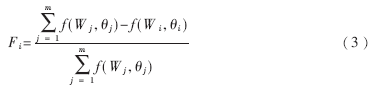
　　式中m为群体个数。第i个网络的f(Wi，θ_i)的值越小，其适应度Fi越大。

　　(2) 产生祖先。将W，θ的解空间均分，每个区域选取一个点作代表，产生m个原始解。

　　(3)选种评价各W，θ个体的优劣，对适应度Fi的个体赋予其选种概率p(F_i)，实际应用中取0.75～0.95。

　　(4)杂交、突变。突变概率为0.005～0.01。

　　(5)进行父代替换。从父代、子代W、θ的各种取值中依适应度重新排序，取m个适应度大的个体作为下一代的样本，转步骤(3)，直至群体适应度趋于稳定。

　　(6)确定区域收缩方向及区域变化值。群体适应度稳定后，从群体中选取出最佳个体(W₀，θ₀)，并以其负梯度方向作为区域收缩方向(梯度计算方法同BP算法一致)，以最佳个体为中心，沿区域收缩方向按一定比例缩减搜索空间。

(7)得到最佳权值分布。当搜索空间减至一定范围且最优适应度及群体适应度趋于稳定时，即得到最佳W0，θ₀。

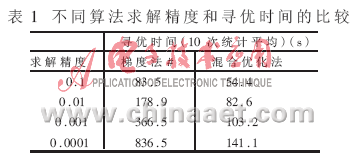
在网络模型为5-11-1，13组训练样本情况下，BP网络优化前后收敛速度的比较如表1所示。

　　已知序列{X₁}，{X₂}，…，{X_t-1}，为了预测{X_t}，根据神经网络预测方法和神经网络的特性，我们可以将神经网络预测模型用如下预测方程表示:

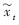　　为预测值，x_t为实测值。

　　要建立良好的预测模型，就是要使预测误差为最小。可以看到(6)式正是神经网络的能量函数。神经网络的训练过程就是使预测误差达到全局最小的过程，也是预测模型的建立过程，它是靠训练样本驱动的。神经网络建模的最终结果是求出非线性函数f_i(x)。而f_i(x)是以网络模型各节点的连接权值和阈值来表达的，通常为单边S型函数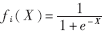。结合本人工作实际，选取作用函数为对称S型函数。

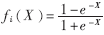　　根据已有的样本数据对网络进行训练，若希望用过去的n(n≥1)个数据预测未来m(m≥1)个时刻的值，即进行m步预测，可取序列中n个相邻的样本为滑动窗并将它们映射为m个值。这m个值代表在该窗之后的m个时间上的样本预测值。表2列出了训练数据的一种分段方法。把训练数据分成k段长度为n+m的有一定重叠的数据段，每一段的头n个数据作为网络的输入，后m个数据则作为相应的网络输出。

1.1 基于单因素输入的单变量神经网络预测器

    本文采用三层前馈网络模型(BP模型)。如图1所示，网络的输入层有n(n≥1)个节点，输出层有m(m≥1)个节点，隐含层节点数n₁由所分析时间序列的复杂程度、预测精度和训练样本的多少而定。

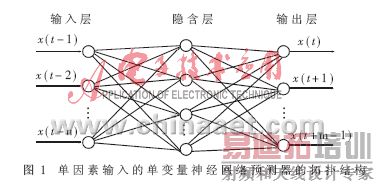
    选用三层BP网络模型进行预测的具体步骤为:

　　(1)根据预测问题的要求，确定网络的模型结构(n-n1-m)和学习参数;

　　(2)采集信号，提取特征参数得到时间序列，对时间序列进行预处理，以便提高网络的预测精度和稳定性;

　　(3)用表2方法确定训练样本集，对网络进行训练以满足预测精度要求;

　　(4)用训练得到的网络进行预测，用预测误差评价预测结果。

1.2 基于多因素输入的单变量神经网络预测器

　　网络的输出为P(t);隐含层的节点数同样要由所分析的时间序列的复杂程度、样本的多少及要求的预测精度来确定。其拓扑结构如图2所示。

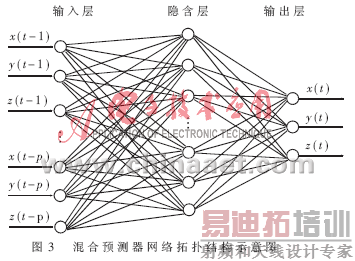
1.3 多变量时间序列的神经网络预测器

　　多变量时间序列分析对于研究时间序列的预测问题来说是一个重要的统计学手段。它通过同时研究许多相关的变量而不是单一变量，往往能够获得更好的预测效果。一个多变量时间序列是由几个随时间同时变化的变量的值序列组成的，而且被测量的变量相互之间有较大的联系。在预测某个变量的新值时，如果也考虑其他变量的变化，就会得到较好的预测。传统的多变量时间序列分析基本上都假设变量之间是线性的关系。在现实中，时间变量之间并不呈现简单的线性规律，所以将非线性模型用于实际的时间序列分析是必要的。

　　本文采用多变量时间序列的神经网络预测器即神经网络混合预测器。n个变量的网络预测模型表示为:

2 基于神经网络预测器的传感器数据证实技术及其实例研究

　　建立传感器输出信号的神经网络预测器模型之后，实际应用时，利用传感器实际输出的前m步样本x(n-m+1)，x(n-m+2)，...，x(n)预测传感器第n+1步输出x^(n+1)，进而利用传感器预测输出值与传感器实际输出进行比较，传感器数据的可靠性和有效性就得到了证实。预测器模型如图4所示。

    为验证上述各种神经网络预测器的有效性及其预测性能，采用日常生活中常见的正弦信号进行上述几种方法的预测，并用单因素输入的神经网络预测法对齿轮实验台实际采集的齿轮振动信号进行预测(实验装置见图7)。     

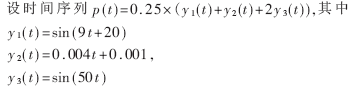
    对于单因素输入神经网络预测器，拓扑结构为9-19-6的预测模型，拟合误差为0.00498，预测结果如图5所示;对于多因素输入神经网络预测器，拓扑结构为12-25-6的预测模型，输入为p(t)，y₁(t)，y₂(t)，y₃(t)，拟合误差为0.00497，预测结果如图5所示;对于多变量时间序列的神经网络预测器，拓扑结构为12-25-6的预测模型，输入为p(t)，y₁(t)，y₂(t)，y3(t)，输出为p(t)和y₁(t)，拟合误差为0.00487，预测结果如图6所示。同样利用神经网络对齿轮实验台的振动加速度传感器输出信号进行预测，网络结构为9-19-6，拟合误差为0.0042，预测结果如图8所示。从图5、图6、图8中可以看出:只要选择合适的神经网络预测模型和网络拟合精度，就可以比较精确地进行预测。

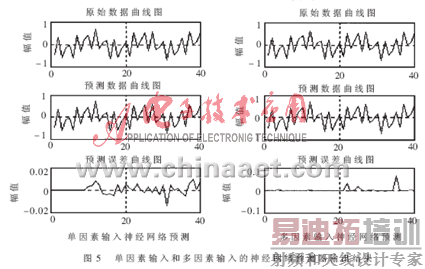
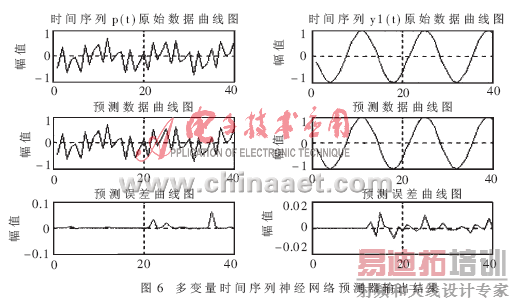
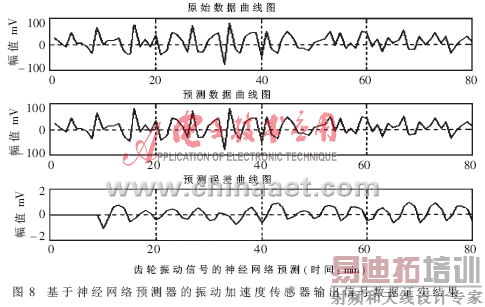
　　图7为一封闭式齿轮实验台，它通过直流调速电机驱动，可以在运行过程中进行变速，主轴的转速可通过光电编码器测出。在陪试齿轮箱和测试齿轮箱之间作用一封闭扭矩，在运行过程中可通过螺旋加载器进行正反向变载，同时，其齿轮间的封闭扭矩和电机扭矩可通过扭矩传感器测出。在实验中选用两个B&K4368振动加速度计和YE5858电荷放大器，多路信号同时通过TEAC磁带记录仪进行记录，经低通滤波器9B02滤波(截止频率为2kHz)后，通过研华AD818HG采集板以5kHz的采样频率进行信号采集(输出为电压信号)。

从实际应用中，可以得出:

　　(1)具有较完备训练样本集的神经网络预测器的预测精度高，基于高精度神经网络预测器的传感器数据证实的可靠性和有效性也相应提高。

　　(2)神经网络预测器的模型建立，一般需要相对较长的时间。采用遗传算法可以大大缩短这一进程的时间，满足在线应用的需要。

　　(3)建立神经网络预测器模型利用了传感器正常运行时的数据信息，用来训练神经网络预测器的样本应能反映传感器正常测量数据。

　　(4)利用本文提出的方法，不仅可以对传感器输出数据进行证实，还可以预测传感器“软故障”的发展趋势。

参考文献

1 刘 勇，康立山，陈毓屏.非数值并行算法——遗传算法.北京:科学出版社，1997;137～154

2 吴祖堂.机械设备状态预测与诊断方法研究及应用.国防科技大学硕士学位论文，1998.1

3 张 晨，韩月秋.基于神经网络的传感器故障诊断技术. 电子科技导报，1998(8):23～26

4 宋 刚，黄善衡.基于神经网络的传感器在线诊断系统.气轮机技术，1998(8):210～213