- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
TD-SCDMA系统智能天线的重复迭代自适应算法
录入：edatop.com 点击：
摘 要：提出一种用于TD-SCDMA系统的重复迭代自适应智能天线算法。通过在自适应算法中把阵列输入信号和作为参考信号的训练序列重复使用，可以在短训练序列情况下实现较好的收敛，提高通信系统的传输效率。对LMS算法中全训练序列重复迭代和滑动窗口重复迭代算法进行了仿真，结果表明，在有限训练序列时本算法比传统LMS算法更好地逼近最佳解。
关键词：移动通信；天线阵列；智能天线；自适应算法
一、引言
智能天线由于其良好的抗多用户干扰和多径干扰性能成为近年来人们关注的热点［1，2］。尤其是对于主要采用CDMA技术的3G移动通信系统，由于多用户干扰是限制系统性能的主要因素，智能天线良好的抗多用户干扰性能使其成为3G移动通信系统关键技术之一。对于CDMA系统，人们一直都在寻找高效精确的控制算法，已提出了不少方案［3~6］，主要可以分为盲控制算法和非盲控制算法两类。前者不需要系统提供参考信号，如文献［4］中提出的LS-DRMTA(Least Squares De-spread Re-spread Multitarget Array)和LS-DRMTACMA(Least Squares De-spread Re-spread Multitarget Constant Modulus Algorithm)算法；后者需要系统提供参考信号，通常可采用系统的导频信号或训练序列作为智能天线的参考信号，如LMS算法、RLS算法和文献［6］介绍的PSALS-SDRMTA(Pilot symbol-assisted least square error de-scramble de-spread re-spread multitarget array)算法。由于非盲算法简单可靠，因此人们总是想办法利用信号帧结构特点，在导频信号或训练序列期间采用非盲的自适应算法［6，7］。在TD-SCDMA系统中以10 ms为一个帧，每个帧又分为2个5 ms的子帧，每个子帧分为7个时隙，每个时隙都含有144 chip的训练序列（midamble）［8］。不同用户的训练序列是不同的，可以作为自适应智能天线的参考信号。出于传输效率的考虑，移动通信系统中的训练序列或导频信号都不会太长（对于TD-SCDMA只有144个码片）。对于采用迭代方式的自适应算法（如LMS、RLS等），短的训练序列会限制迭代步数。如何在比较短的训练序列期间实现比较好的收敛是实现TD-SCDMA系统中非盲智能天线算法必须考虑的问题。针对这一问题，本文提出了重复迭代自适应智能天线算法，即把训练序列期间接收到的阵列输入信号和对应的参考信号（已知的训练序列）周期扩展成长的序列，使迭代步数加大，从而可以实现比较好的收敛。为了平衡计算速度、存储空间和收敛速度的矛盾，本文还给出了滑动窗口重复迭代自适应算法。以LMS算法为例的仿真结果表明本文给出的方法可以在比较短的训练序列情况下达到比较好的收敛。
二、重复迭代自适应智能天线算法
在自适应智能天线中，自适应算法是其基本的控制算法。对于LMS或RLS自适应阵，采用最小均方误差（MMSE）准则，使阵列输出与参考信号的误差功率最小。设x(j)为阵列输入矢量，r(j)为期望的阵列输出信号（参考信号），最佳权系数的解为
式中R是阵列输入矢量的相关矩阵，P是阵列输入矢量与参考信号的互相关矢量。
在TD-SCDMA系统中，由于每时隙的训练序列只有144个码片（chip），因此我们只有有限长的参考信号进行自适应控制，这时我们采用的自适用控制准则实际上只能是使有限数据长度x(j)和r(j）下的平均误差功率最小，即只能得到次最优解。这时，式（1）中相关矩阵R和互相关矢量p只能用有限长度的阵列输入矢量和参考信号来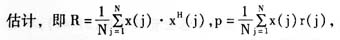
N是数据长度。如果在TD-SCDMA系统中利用训练序列（midamble）进行MMSE准则的自适应控制，则N可取144。
直接采用式（1）计算阵列权系数涉及矩阵求逆运算，计算量和占用存储空间大，通常采用迭代算法（如LMS、RLS算法）。受有限参考信号长度的限制，迭代步数不能太多（对于TD-SCDMA，只有144个码片的训练序列），即使是次最优解，LMS、RLS算法也无法达到。为了解决这一问题，我们提出了数据重用的重复迭代自适应算法，包括整段训练序列的重复迭代算法和滑动窗口重复迭代算法。
整段训练序列的重复迭代算法把训练序列和阵列输入序列周期扩展为长的序列，使迭代步数加大，便于逼近次最佳权值。代价是需要更多的存储空间储存N个阵列输入矢量和参考信号，以及计算时间相应加大。但采用重复迭代自适应算法后可使收敛程度改善，更好地逼近次最优解。
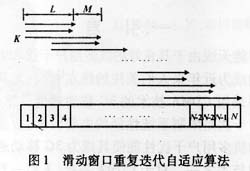
把整段训列序列期间的数据重复使用需要的存储空间较大，同时不利于跟踪快速变化的信道，也需要较快的运算速度以便在短的时间内完成整段数据的多次迭代。为了平衡收敛性能和存储空间、运算速度及跟踪性能的矛盾，我们提出滑动窗口重复迭代算法,即每次从阵列输入和训练序列截取长度为L的一段数据重复迭代K次，当有M个新数据加入时，把最旧的M个数据丢掉，从新在新的长度为L的一个窗口上进行重复迭代。随着新数据的不断加入，重复迭代窗口也不断向前滑动，如图1所示。由于多了窗口长度L、每窗口重复次数K、窗口滑动间隔M等参数的控制，可以比较方便地平衡收敛程度、跟踪速度、存储空间及运算速度的矛盾。如果取L=N、M=0，则变为整段训练序列的重复迭代算法。
三、仿真结果
为了验证提出的算法，我们对LMS自适应阵列进行了仿真。仿真采用间距为半波长8元直线阵列，用户数为8个，设采用了理想的功率控制，各用户到达阵列的信号幅度都为1，各用户的波达方向分别为60°、100°、20°、150°、175°、90°、15°、130°。作为仿真，各用户的训练序列数据随机产生，长度144点，学习率为0.005，设第1个用户为期望用户。图2和图3分别为全训练序列（144 chip）循环1次和20次后形成的方向性图。由图2和图3可见，方向性图最大方向都对准了期望用户的来波方向（60°），干扰方向都可以形成下陷，但循环多次的方向性图在干扰方向下陷得更深，表明在短数据长度时，对数据重复循环使用可提高收敛程度。为了比较，图4给出传统LMS算法的方向性图，采用2 880个数据进行随机梯度LMS算法，对比表明循环多次的方向性图逼近最优结果。图5给出了重复迭代20次的LMS算法的收敛曲线。由图5可看到，重复1次（迭代144步）的误差还比较大，即使重复3次（迭代432步）还没有完全收敛，因此还没有收敛到次最优权系数。多次重复迭代后，收敛曲线趋于稳定，表明采用重复迭代算法可以在短数据长度达到次最优结果。
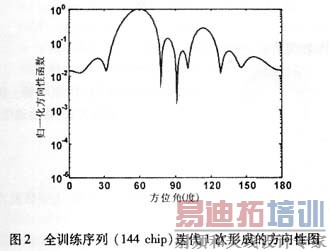
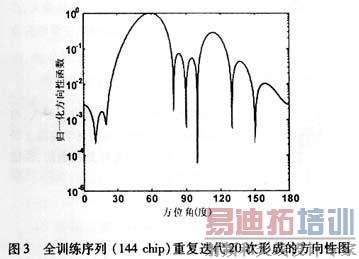
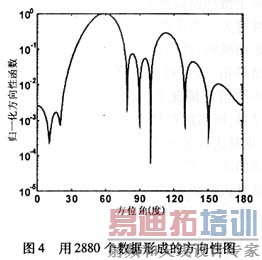
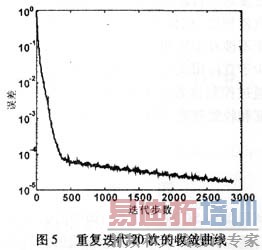
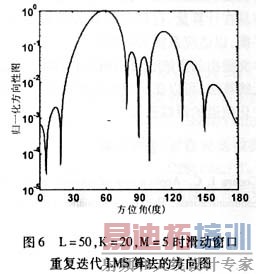
图6给出了采用滑动窗口重复迭代LMS算法的仿真结果。天线阵列和信号情况与前面一样，训练序列长度为TD-SCDMA时隙结构的144 chip，学习率取0.005。滑动参数为L=50，K=20，M=5。图中可见，方向性图最大方向都对准了期望用户的来波方向（60°），干扰方向都可以形成下陷。和图2只迭代一次的方向性图相比，干扰方向下陷得更深，逼近图4给出的长数据迭代结果，表明在短数据长度，采用滑动窗口重复迭代使用可提高收敛程度，逼近次最佳结果。
对于滑动窗口重复迭代算法，窗口长度L与跟踪特性有关。由于在窗口长度L内多次迭代，旧数据的影响减弱，其逼近的结果与数据长度为L的次最佳结果相近，这样有利于跟踪快速变化的信道。在时不变信道情况下，窗口长度L越大，越接近次最优结果，所需的存储空间越大。对于时变信道，L越小，重复次数K越多，滑动距离M越大，越容易跟踪信道的变化，所需的存储空间越小。
重复次数影响计算量和收敛程度，重复次数越多，收敛越好，计算量越大。通过控制重复次数可以根据实际情况平衡计算速度与收敛特性。
重复迭代自适应算法通过对短数据重复迭代来提高收敛程度，代价是增加了计算量和存储空间。但由于不涉及矩阵相乘和矩阵求逆等运算，计算量还是少于直接用式（1）的矩阵求逆方法来计算。特别是通过控制参数L、K和M，可以平衡计算量、跟踪速度和收敛程度，更好地适应通信系统具体的情况。
四、结束语
利用TD-SCDMA信道结构中的训练序列进行非盲自适应控制可以降低智能天线的控制算法的复杂度，然而出于通信效率的考虑，TD-SCDMA上行信道的训练序列只有144个码片，传统的迭代算法迭代步数受到限制，无法达到最佳的结果。本文提出的重复迭代算法通过把TD-SCDMA信道中训练序列及其对应阵列输入数据重复使用加大迭代步数，可以在短的数据长度下逼近最佳结果。以LMS算法为例的仿真结果表明该方法是可行的，可以有效改善TD-SCDMA系统智能天线的性能。通过控制窗口长度、重复次数和窗口滑动间隔，本文提出的方法容易在计算量、存储空间及智能天线性能之间取得平衡，以适应系统实际情况。
本文提出的方法也可以推广到其他迭代方式的智能天线算法，可以在比较短的数据下实现收敛，提高对变化信道的跟踪速度。
参考文献
［1］Godara L C.Applications of antenna arrays to mobile communications, Part I: performance improvement , feasibility, and system considerations［Ｊ］. Proceedings of the IEEE, 1997, 85(7)：1031～1060.
［2］John L,Lo T K. Digital beamforming in wireless communication［M］.MA: Artech House, 1996.
［3］Wang Y,Gruz J R. Adaptive antenna arrays for cellular CDMA communication systems［A］. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processign［C］. Piscataway：IEEE,1995.1725~1728.
［4］Rong Z,Pertrus P, Rappaport T S,et al. Despread-respread multi-target constant modulus array for CDMA systems［J］. IEEE Communications Letters,1997, 1(4):114~116.
［5］RONG Z, RAPPORT T S. Simulation of multitarget adaptive algorithms for wireless CDMA systems［A］.Proceedings of IEEE Vehicular Technology Conference［C］. Pisacataway: IEEE, 1996.1~5.
［6］丁杰伟，李鲲鹏，黄超，等.WCDMA系统中智能天线PSALS-SDRMTA自适应算法［J］.通信学报，2003，24（2）：78~83.
［7］孟维晓，张乃通. 时分双工蜂窝系统的智能天线研究和性能评估［J］. 通信学报，2000，21（10）：73～80.
［8］孙立新，尤肖虎，张萍，等. 第三代移动通信技术［M］.北京：人民邮电出版社，2000.
作者：
谢泽明1，赖声礼1，陈一天2，余爱民2
（1．华南理工大学 电子与信息学院，广东 广州510640；2．广东省科技干部学院，广东 广州510640） 来源：电讯技术
关键词：移动通信；天线阵列；智能天线；自适应算法
一、引言
智能天线由于其良好的抗多用户干扰和多径干扰性能成为近年来人们关注的热点［1，2］。尤其是对于主要采用CDMA技术的3G移动通信系统，由于多用户干扰是限制系统性能的主要因素，智能天线良好的抗多用户干扰性能使其成为3G移动通信系统关键技术之一。对于CDMA系统，人们一直都在寻找高效精确的控制算法，已提出了不少方案［3~6］，主要可以分为盲控制算法和非盲控制算法两类。前者不需要系统提供参考信号，如文献［4］中提出的LS-DRMTA(Least Squares De-spread Re-spread Multitarget Array)和LS-DRMTACMA(Least Squares De-spread Re-spread Multitarget Constant Modulus Algorithm)算法；后者需要系统提供参考信号，通常可采用系统的导频信号或训练序列作为智能天线的参考信号，如LMS算法、RLS算法和文献［6］介绍的PSALS-SDRMTA(Pilot symbol-assisted least square error de-scramble de-spread re-spread multitarget array)算法。由于非盲算法简单可靠，因此人们总是想办法利用信号帧结构特点，在导频信号或训练序列期间采用非盲的自适应算法［6，7］。在TD-SCDMA系统中以10 ms为一个帧，每个帧又分为2个5 ms的子帧，每个子帧分为7个时隙，每个时隙都含有144 chip的训练序列（midamble）［8］。不同用户的训练序列是不同的，可以作为自适应智能天线的参考信号。出于传输效率的考虑，移动通信系统中的训练序列或导频信号都不会太长（对于TD-SCDMA只有144个码片）。对于采用迭代方式的自适应算法（如LMS、RLS等），短的训练序列会限制迭代步数。如何在比较短的训练序列期间实现比较好的收敛是实现TD-SCDMA系统中非盲智能天线算法必须考虑的问题。针对这一问题，本文提出了重复迭代自适应智能天线算法，即把训练序列期间接收到的阵列输入信号和对应的参考信号（已知的训练序列）周期扩展成长的序列，使迭代步数加大，从而可以实现比较好的收敛。为了平衡计算速度、存储空间和收敛速度的矛盾，本文还给出了滑动窗口重复迭代自适应算法。以LMS算法为例的仿真结果表明本文给出的方法可以在比较短的训练序列情况下达到比较好的收敛。
二、重复迭代自适应智能天线算法
在自适应智能天线中，自适应算法是其基本的控制算法。对于LMS或RLS自适应阵，采用最小均方误差（MMSE）准则，使阵列输出与参考信号的误差功率最小。设x(j)为阵列输入矢量，r(j)为期望的阵列输出信号（参考信号），最佳权系数的解为
式中R是阵列输入矢量的相关矩阵，P是阵列输入矢量与参考信号的互相关矢量。
在TD-SCDMA系统中，由于每时隙的训练序列只有144个码片（chip），因此我们只有有限长的参考信号进行自适应控制，这时我们采用的自适用控制准则实际上只能是使有限数据长度x(j)和r(j）下的平均误差功率最小，即只能得到次最优解。这时，式（1）中相关矩阵R和互相关矢量p只能用有限长度的阵列输入矢量和参考信号来
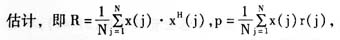N是数据长度。如果在TD-SCDMA系统中利用训练序列（midamble）进行MMSE准则的自适应控制，则N可取144。直接采用式（1）计算阵列权系数涉及矩阵求逆运算，计算量和占用存储空间大，通常采用迭代算法（如LMS、RLS算法）。受有限参考信号长度的限制，迭代步数不能太多（对于TD-SCDMA，只有144个码片的训练序列），即使是次最优解，LMS、RLS算法也无法达到。为了解决这一问题，我们提出了数据重用的重复迭代自适应算法，包括整段训练序列的重复迭代算法和滑动窗口重复迭代算法。
整段训练序列的重复迭代算法把训练序列和阵列输入序列周期扩展为长的序列，使迭代步数加大，便于逼近次最佳权值。代价是需要更多的存储空间储存N个阵列输入矢量和参考信号，以及计算时间相应加大。但采用重复迭代自适应算法后可使收敛程度改善，更好地逼近次最优解。
把整段训列序列期间的数据重复使用需要的存储空间较大，同时不利于跟踪快速变化的信道，也需要较快的运算速度以便在短的时间内完成整段数据的多次迭代。为了平衡收敛性能和存储空间、运算速度及跟踪性能的矛盾，我们提出滑动窗口重复迭代算法,即每次从阵列输入和训练序列截取长度为L的一段数据重复迭代K次，当有M个新数据加入时，把最旧的M个数据丢掉，从新在新的长度为L的一个窗口上进行重复迭代。随着新数据的不断加入，重复迭代窗口也不断向前滑动，如图1所示。由于多了窗口长度L、每窗口重复次数K、窗口滑动间隔M等参数的控制，可以比较方便地平衡收敛程度、跟踪速度、存储空间及运算速度的矛盾。如果取L=N、M=0，则变为整段训练序列的重复迭代算法。
三、仿真结果
为了验证提出的算法，我们对LMS自适应阵列进行了仿真。仿真采用间距为半波长8元直线阵列，用户数为8个，设采用了理想的功率控制，各用户到达阵列的信号幅度都为1，各用户的波达方向分别为60°、100°、20°、150°、175°、90°、15°、130°。作为仿真，各用户的训练序列数据随机产生，长度144点，学习率为0.005，设第1个用户为期望用户。图2和图3分别为全训练序列（144 chip）循环1次和20次后形成的方向性图。由图2和图3可见，方向性图最大方向都对准了期望用户的来波方向（60°），干扰方向都可以形成下陷，但循环多次的方向性图在干扰方向下陷得更深，表明在短数据长度时，对数据重复循环使用可提高收敛程度。为了比较，图4给出传统LMS算法的方向性图，采用2 880个数据进行随机梯度LMS算法，对比表明循环多次的方向性图逼近最优结果。图5给出了重复迭代20次的LMS算法的收敛曲线。由图5可看到，重复1次（迭代144步）的误差还比较大，即使重复3次（迭代432步）还没有完全收敛，因此还没有收敛到次最优权系数。多次重复迭代后，收敛曲线趋于稳定，表明采用重复迭代算法可以在短数据长度达到次最优结果。
图6给出了采用滑动窗口重复迭代LMS算法的仿真结果。天线阵列和信号情况与前面一样，训练序列长度为TD-SCDMA时隙结构的144 chip，学习率取0.005。滑动参数为L=50，K=20，M=5。图中可见，方向性图最大方向都对准了期望用户的来波方向（60°），干扰方向都可以形成下陷。和图2只迭代一次的方向性图相比，干扰方向下陷得更深，逼近图4给出的长数据迭代结果，表明在短数据长度，采用滑动窗口重复迭代使用可提高收敛程度，逼近次最佳结果。
对于滑动窗口重复迭代算法，窗口长度L与跟踪特性有关。由于在窗口长度L内多次迭代，旧数据的影响减弱，其逼近的结果与数据长度为L的次最佳结果相近，这样有利于跟踪快速变化的信道。在时不变信道情况下，窗口长度L越大，越接近次最优结果，所需的存储空间越大。对于时变信道，L越小，重复次数K越多，滑动距离M越大，越容易跟踪信道的变化，所需的存储空间越小。
重复次数影响计算量和收敛程度，重复次数越多，收敛越好，计算量越大。通过控制重复次数可以根据实际情况平衡计算速度与收敛特性。
重复迭代自适应算法通过对短数据重复迭代来提高收敛程度，代价是增加了计算量和存储空间。但由于不涉及矩阵相乘和矩阵求逆等运算，计算量还是少于直接用式（1）的矩阵求逆方法来计算。特别是通过控制参数L、K和M，可以平衡计算量、跟踪速度和收敛程度，更好地适应通信系统具体的情况。
四、结束语
利用TD-SCDMA信道结构中的训练序列进行非盲自适应控制可以降低智能天线的控制算法的复杂度，然而出于通信效率的考虑，TD-SCDMA上行信道的训练序列只有144个码片，传统的迭代算法迭代步数受到限制，无法达到最佳的结果。本文提出的重复迭代算法通过把TD-SCDMA信道中训练序列及其对应阵列输入数据重复使用加大迭代步数，可以在短的数据长度下逼近最佳结果。以LMS算法为例的仿真结果表明该方法是可行的，可以有效改善TD-SCDMA系统智能天线的性能。通过控制窗口长度、重复次数和窗口滑动间隔，本文提出的方法容易在计算量、存储空间及智能天线性能之间取得平衡，以适应系统实际情况。
本文提出的方法也可以推广到其他迭代方式的智能天线算法，可以在比较短的数据下实现收敛，提高对变化信道的跟踪速度。
参考文献
［1］Godara L C.Applications of antenna arrays to mobile communications, Part I: performance improvement , feasibility, and system considerations［Ｊ］. Proceedings of the IEEE, 1997, 85(7)：1031～1060.
［2］John L,Lo T K. Digital beamforming in wireless communication［M］.MA: Artech House, 1996.
［3］Wang Y,Gruz J R. Adaptive antenna arrays for cellular CDMA communication systems［A］. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processign［C］. Piscataway：IEEE,1995.1725~1728.
［4］Rong Z,Pertrus P, Rappaport T S,et al. Despread-respread multi-target constant modulus array for CDMA systems［J］. IEEE Communications Letters,1997, 1(4):114~116.
［5］RONG Z, RAPPORT T S. Simulation of multitarget adaptive algorithms for wireless CDMA systems［A］.Proceedings of IEEE Vehicular Technology Conference［C］. Pisacataway: IEEE, 1996.1~5.
［6］丁杰伟，李鲲鹏，黄超，等.WCDMA系统中智能天线PSALS-SDRMTA自适应算法［J］.通信学报，2003，24（2）：78~83.
［7］孟维晓，张乃通. 时分双工蜂窝系统的智能天线研究和性能评估［J］. 通信学报，2000，21（10）：73～80.
［8］孙立新，尤肖虎，张萍，等. 第三代移动通信技术［M］.北京：人民邮电出版社，2000.
作者：
谢泽明1，赖声礼1，陈一天2，余爱民2
（1．华南理工大学 电子与信息学院，广东 广州510640；2．广东省科技干部学院，广东 广州510640） 来源：电讯技术
上一篇：用电子电路实现通讯继电器的电器特性测试
下一篇：移动电话手机场强仪
