一种基于路由信息的传感网络定位算法

1. 引言

无线传感器网络是近年来一个热点研究领域，其中传感器网络定位技术也越来越受到人们的关注，这是因为传感器网络的大量应用都依赖于节点的位置信息，例如在战场侦察、生态环境监测、地震洪水火灾等现场的监控等应用中，都需要知道传感器节点的位置信息，从而获知信息来源的准确位置。

现有无线传感器网络定位系统种类繁多，实现方法各异[1] [2]。具有代表性的有采用超声波测距的TDOA (Time Difference of Arrival)系统[3]，基于RSSI (Receive Signal Strength Indicator)的技术[4]，基于网络连通性的质心定位算法[5]，基于多跳传感器网络节点间跳数的DV-Hop算法[6]等。现有算法大多存在额外的硬件开销，或需要较多已知位置的参考节点，而且都有较大的通信开销，带来了传感器节点额外的功耗，这样就降低了全网的生存周期。因此，需要针对无线传感器网络的具体场景，设计低成本，低开销，易实现的定位算法。

2. 基于路由信息的定位算法

2.1 研究场景定义

无线传感器网络的应用场景各异，对定位的需求也各不相同。因此，在进行定位算法的设计前，必须选定应用场景进行有针对性的设计。本文选用传感器网络中广泛应用的大范围数据采集场景，例如土壤温湿度监测、森林火险预警、智能大厦人员数据采集等，作为研究前提。

在这种场景下，数量众多的传感器节点分布在较大范围的区域内，节点需要通过多跳路由将数据返回到一个或多个网关节点。所有传感器节点不装配GPS、超声收发器、有向天线等额外的定位和测距设备，节点射频模块只具备射频信号强度检测能力 (RSSI)，甚至RSSI能力也不具备（即只有通信功能）。为了方便下面的研究，进一步对场景作如下简化定义：

1. 传感器节点数目表示为n, 网关节点数目表示为m；

2. n个传感器节点在区域内随机均匀分布，自身位置为(xi, yi)均未知，其中i = 1...n；

3. m个网关节点在区域内以某种规律分布，自身位置(xi, yi)均已知，其中i = n+1...n+m；

4. 传感器节点均以一定且相同的周期采集数据，节点间相对静止；

5. 节点采用无线全向天线进行互通信，RSS测距的先验概率分布满足高斯分布；

2.2 设计思路

而且因为数据采集任务对网络的存活时间要求一般较高，所以降低传感器节点的功耗，即降低传感器节点的通信开销就成为设计定位算法中重要的因素。而现有定位算法存在的主要问题就是通信开销大，其中有一个重要原因是现有的研究将定位过程与网络路由和数据采集看作独立的过程，而事实上这两个过程存在大量通信的重复，这样就带来了额外的通信开销。本文的研究就是将路由协议与定位算法结合来减少这部分开销，基本思路是通过在数据包上附加网络路由信息来获得部分节点间的连接和距离关系，然后根据这些关系来进行传感器节点定位，该算法命名为RBSL (Routing information Based Sensor Localization)。

本文选用了传感器网络中常用的定向扩散路由协议[7] (Directed Diffusion)作为研究的基础。定向扩散路由协议是一种以数据为中心的路由协议，网关节点向所有传感器节点发送对任务描述的"兴趣" (Interest)，"兴趣"会逐渐在全网中扩散，最终达到所有匹配"兴趣"的传感器节点，与此同时也建立起了从网关节点到传感器节点的"梯度"，传感器节点会沿着梯度最大的方向将数据传回网关节点。定向扩散的原理示意图如下图1所示：

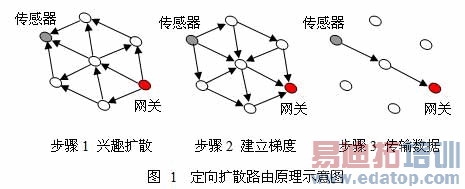
对于全网数据采集的场景，网关节点发送的"兴趣"是采集所有节点数据。在建立梯度之后，每个一个传感器节点都有一个自己对网关节点的最大"梯度"方向，即下一跳传输的目的节点编号 (ID)。若每个传感器节点在发送数据包末尾都附加自己的下一跳节点ID，则在每一个网关节点就都可以获得网络中n条链路的连接情况，即获得了到一个网关节点的树状路由表。将m个网关节点的数据进行综合就可以获得更多条链路的连接情况。将获得的n个传感器节点和m个网关节点之间的连接关系表示为对称连接矩阵L (n+m,n+m)，其中Lij = 1 表示i, j节点存在路由链路，反之Lij = 0表示不存在路由链路，其中1≤i, j≤ n+m，若1≤i≤n表示i为传感器节点，若n
进一步的，如果传感器节点具有RSSI，可以根据射频信号传输的经验模型估计链路距离dij，同样将估计距离发往网关节点。与连接矩阵L类似可以生成对称距离矩阵，表示为D (n+m,n+m)，其中Dij = Dji 表示i, j节点间路由链路的估计距离。

下一步就是根据连接矩阵L或距离矩阵D来进行节点定位。这里就需要用到MDS算法，MDS算法的全称是多维标度分析（Multi-Dimensional Scaling），是一种最早应用在计量心理学和生物信息统计中的算法。作为MDS算法的一种简单的应用，若已知二维空间上n个点的两两距离，即完全的距离矩阵LALL(n, n)，则可以反解出这n个点的二维相对拓扑。Yi Shang等人[8]最早将MDS算法应用到无线网络定位中，本文也采用了类似的思路。由于通过路由过程获得的连接矩阵L或距离矩阵D都只是部分链路，所以还需要通过最短路径算法生成在原矩阵中不连通的节点之间的近似距离，得到近似的DALL来作为MDS算法的输入。

在获得距离矩阵DALL之后，就可以根据MDS算法计算得到节点的相对二维拓扑分布，但该分布与真实分布存在缩放，旋转和平移的关系。因为m个网关节点都已知自身位置，当m≥3时，可以根据网关节点的位置，对相对拓扑进行坐标变换得到最终估计的二维拓扑。

3. 算法实现过程

3.1 定向扩散

目的是尽可能多的携带节点间的连接或测距信息，在建立梯度阶段中，每个节点可以得到其下一跳节点ID。在传输数据阶段，则将下一跳节点ID也打入数据包，按照最大梯度方向发往网关节点。当节点具有RSSI时，还要将下一跳节点对应的测距结果发往网关节点。

3.2 计算节点距离矩阵DALL

目的是提取网关数据中关于节点连接或测距的信息，并通过最短路径算法得到所有节点间的近似距离，即完全的距离矩阵。当节点具有RSSI时，则可以根据数据包中的每个节点的测距信息生成部分距离矩阵D，然后采用Floyd最短路径算法，生成DALL。若节点不具备RSSI，则将连通表示为单位距离1，同样用Floyd最短路径算法，由连接矩阵L生成DALL。

3.3 多维标度分析MDS

将节点距离矩阵DALL作为MDS算法的输入矩阵，可以获得节点的相对位置估计X ’, Y ’。

3.4 平移和旋转变换

通过比对已知位置的网关节点，将MDS结果进行坐标变换使得网关位置均方误差最小。即设X’, Y’为MDS输出的网关节点位置，求变换矩阵A, B使得[X’’, Y’’] = A * [X’, Y’] + B与网关节点已知位置[X, Y]的均方误差最小。

来源：中电网