软件定义仪器的数字化前端和ADC 的等效分辨率

     对于理想的ADC 和幅度变化缓慢的输入信号， 量化噪声不能看作为白噪声，但是为了利用白噪声的理论，在输入信号上叠加一个连续变化的信号，这时利用过采样技术提高信噪比，即过采样后信号和噪声功率不发生改变，但是噪声功率分布频带展宽，通过下抽取滤波后，噪声功率减小，达到提高信噪比的效果，从而提高ADC 的分辨率。

　　Σ-Δ 型ADC 实际采用的是过采样技术，以高速抽样率来换取高位量化，即以速度来换取精度的方案。与一般ADC不同，Σ-Δ 型ADC 不是根据抽样数据的每一个样值的大小量化编码，而是根据前一个量值与后一量值的差值即所谓的增量来进行量化编码。Σ-Δ 型ADC 由模拟Σ-Δ 调制器和数字抽取滤波器组成， Σ-Δ 调制器以极高的抽样频率对输入模拟信号进行抽样， 并对两个抽样之间的差值进行低位量化，得到用低位数码表示的Σ-Δ 码流，然后将这种Σ-Δ 码送给第2 部分的数字抽取滤波器进行抽样滤波，从而得到高分辨率的线性脉冲编码调制的数字信号。

　　然而，Σ-Δ 型ADC 在原理上，过采样率受到限制，不可无限制提高，从而使得真正达到高分辨率时的采样速率只有几赫兹到几十赫兹，使之只能用于低频信号的测量。

　　高速中分辨率的ADC 用过采样产生等效分辨率和Σ-Δ型ADC 的高分辨率在原理上基本是一样的， 因此本文在归一化条件下提出的ADC 等效分辨率公式既可以作为*估数字化前端ADC 的一个通用性能参数， 又可作为ADC 选用的参考依据。

　　2.2 ADC 等效分辨率

　　与输入信号一起，叠加的噪声信号在有用的测量频带内（小于fs/2 的频率成分）即带内噪声产生的能量谱密度为：

　　式中，erms为平均噪声功率；E（f）为能量谱密度（ESD）。两个相邻的ADC 码之间的距离决定量化误差的大小，有相邻ADC 码之间的距离表达式为：

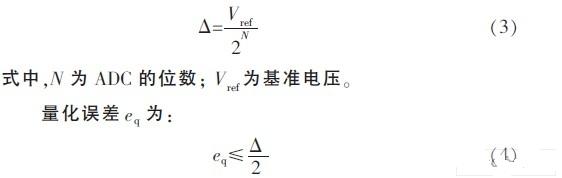
　　设噪声近似为均匀分布的白噪声，则方差为平均噪声功率，表达式为：

　　用过采样比[OSR]表示采样频率与奈奎斯特采样频率之间的关系，其定义为：

　　如果噪声为白噪声，则低通滤波器输出端的带内噪声功率为：

　　式中，n0为滤波器输出的噪声功率。

　　由式（3）、式（5）、式（7）可推出噪声功率[OSR]和分辨率的函数，表示为：

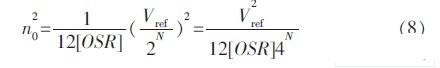
　　为得到最佳的[RSN]，输入信号的动态范围必须与参考电压Vref相适应。假设输入信号为一个满幅的正弦波，其有效值为：

　当[OSR]=1 时，为未进行过采样的信噪比，可见过采样技术增加的信噪比为：

　　香农限带高斯白噪声信道的容量公式为：

　　其中，W 为带宽。

　　式（13）描述了有限带宽、有随机热噪声、信道最大传输速率与信道带宽信号噪声功率比之间的关系， 式（13） 可变为：

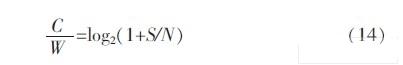
　　式（14）用来描述系统单位带宽的容量，单位为b/（s·Hz）。将式（10）代入式（14）中，得：

　　其中，fs为归一化频率下的采样速率。

　　综上可知， 在已知ADC 归一化采样频率后便可根据等效分辨率式（17），得到ADC 所能提供的最大等效分辨率，以指导正确选择和有效利用ADC， 充分利用其速度换取分辨率，分辨率进一步可以换取信号增益，足够高的分辨率可以代替信号的模拟放大电路，从而简化软件仪器的数字化前端设计，方便仪器功能的软件定义。

　　3 等效分辨率的应用

　　3.1 ADC 的选择

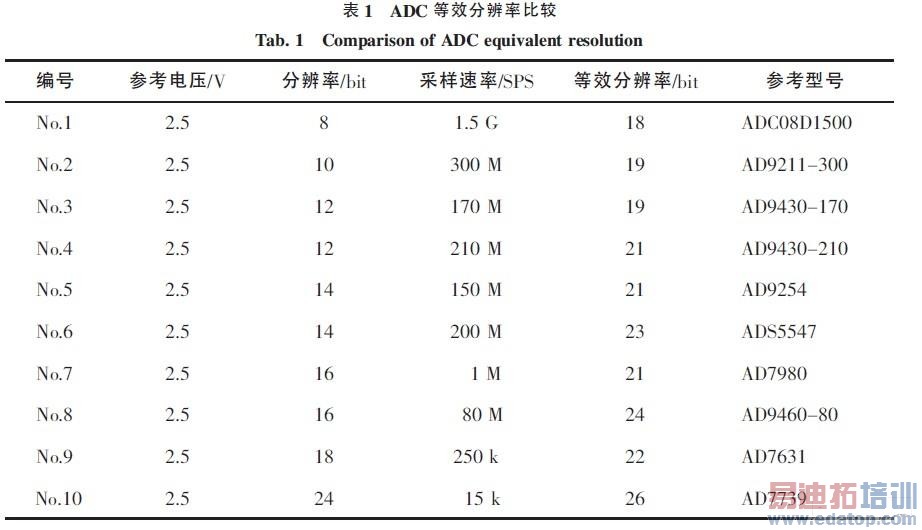
　　表1 为10 款ADC 的参数和由式（17）计算出的等效分辨率。由表1 可知，No.10 的等效分辨率最高，因此，仅从等效分辨率来看AD7739 是设计数字化前端的最优选择， 但考虑其采样速率较低，No.6 和No.8 也可以作为优选的型号。总而言之， 选择ADC 时主要参考其等效分辨率和采样速率这两个参数，No.6、No.8 和No.10 均在考虑之列， 其中前二者采样速率较高，适用于中、高频信号；后者采样速率较低，只能用于低频信号的测量。