边缘检测算法在医学超声液性病变 像中的应用

Canny算子检测边缘的实质是求信号函数的极大值问题来判定图像边缘像素点。基本步骤为：
(1)用高斯滤波器平滑图像；
(2)用一阶偏导的有限差分来计算梯度的幅值和方向；
(3)对梯度幅值进行非极大值抑制；
(4)用双阈值算法检测和连接边缘。Canny算子能够得到连续完整的图像，但需要注意的问题是：Gauss滤波的尺度，以及双阈值的选择。
1．4 基于Snake模型的边缘检测算法
Snake模型是1987年由Kass提出的，它的基本思想是以构成一定形状的控制曲线为模板(或者称为轮廓线)，通过模板自身的弹性形变与图像局部特征相匹配达到调和，即某种能量函数极小化，完成对图像边缘的提取，通过对模板的进一步分析而实现图像的理解和识别。能量最小化模型已经有了很长的发展历史，Kass对其进行了改进，采用动态调整的方法来实现它，对图像的高层信息进行分析和提取而不至于受到太多低层信息的影响。通过在原始的最小化函数中加入外力因子，可以引导初始化的轮廓线朝着特定的方向前进，最后达到提取目标边界的目的。
1．4．1 基本Snake模型
Kass等提出的基本Snake模型由一组控制点组成，即v(s)=(x(s)，y(s))，s∈[0，1]，其中x(s)和y(s)分别表示每个控制点在图像中的坐标位置，s是以傅立叶变换形式描述边界的自变量。其对应的能量函数定义为：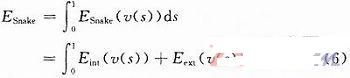


式中：Eint为曲线的内部能量；Eext为外部能量。
内部能量定义为：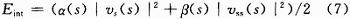


式中|vs(s)|为弹性能量，是曲线相对于弧长的一阶导数的模，受弹性系数的调节，控制着曲线的张力。|vss(s)|是弯曲能量，是曲线相对于弧长的二阶导数的模，受刚性系数的调节，控制曲线的变形程度。
对于普通的灰度图像I(x，y)，典型的外部能量(外部力)表达有如下2种定义：


式中▽为梯度算子，是方差为σ的二维高斯函数。在图像边缘区域，图像灰度值的梯度往往较大，取反后计算以满足能量最小的要求。

每一次迭代，曲线的变形是为了使如下的能量函数达到最小化：

弹性能量和弯曲能量合称内部力，内部力用于控制轮廓线的弹性形变，选取适当的参数α(s)和β(s)将能量函数ESnake极小化，所对应的v(s)就是对物体的分割。在能量函数极小化过程中，弹性能量迅速把轮廓线压缩成一个光滑的圆，弯曲能量驱使轮廓线成为光滑曲线或直线，而外部力则使轮廓线向图像的高梯度位置靠拢，基本Snake模型就是在这3个力的联合作用下工作的。
1．4．2 改进的Snake模型
基本Snake模型在应用的时候存在一些缺陷：
(1)要求初始的轮廓线必须与目标边缘非常的接近，这是因为能量函数往往会收敛到一个非期望的局部最小值，如果初始的轮廓线离目标较远，就会使曲线变形到一个无法预计的形状；
(2)基本Snake模型对无法捕获凹陷边界。这样就限制了Snake模型应用到一些存在凹陷区域的图像上。
近年来，针对以上缺陷，许多研究不仅对Snake模型本身的能量函数构造和求解算法作了很大改进，更在其基础上衍生出了许多新轮廓线模型，它们有些在形式上已经与基本Snake相去甚远，而且也要复杂得多，但其指导思想却是一脉相承的。比如，Cohen提出了一种气球力理论，通过使用不同尺度的外力场，增加外力场的捕捉范围，来驱动轮廓线向目标边缘逼近。XuChenyang提出的GVF Snake将梯度矢量场(GVF)代替传统外力场，让曲线随着图像凹陷的部分而发生变形，圈出凹陷的边缘，由于GVF对轮廓线的初始位置不是非常的敏感，尤其对于二值图像，所以它可以很快的收敛到目标边缘，很好地解决了这些问题。
GVF Snake将基本Snake的外部力用扩散方程进行处理，得到整个图像域的梯度向量场作为外部力，经过扩散方程处理后的GVF更加有序，更能体现物体边界的宏观走势。由于GVF不是一个表达式，无法用能量函数的形式求解，因此GVF Snake是利用力的平衡条件进行优化，GVF Snake具有更大的搜索范围，对轮廓线初始位置不敏感，可以分割凹陷的边界，对梯度绝对值的大小乃至噪声具有更好的鲁棒性，而且它还不必预先知道轮廓线是要膨胀还是收缩。
本文将改进的GVF Snake模型应用于医学超声液性病变图像中，并与其他的边缘检测方法进行比较分析。

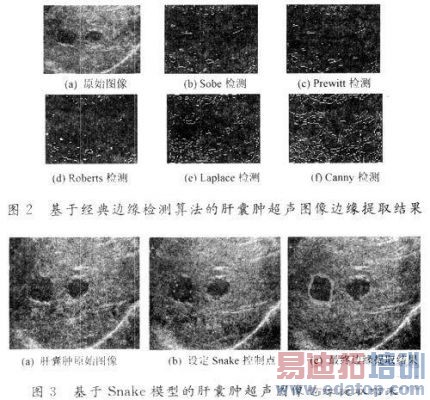
2 实验结果分析
医学超声诊断出的液性病变多以囊肿为主，常见的囊肿有甲状腺囊肿、卵巢囊肿、肝囊肿等，这些超声液性病变图像灰度变化梯度不大，多见数个无回声区，呈"蜂窝状"，边界不清晰。
本文选取两幅具有代表性的肝囊肿、甲状腺囊肿超声液态病变图像，用不同的边缘检测算法对其进行处理，实验结果如图2，图3所示。