- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
物料采购指标权重研究—基于RFID物料管理系统的设计
录入:edatop.com 点击:
物料采购系统中,权重集设计的方法一般有两类:一类是经验判断法,另一类是数理统计和模糊统计法。在设计实践中,常常以经验判断法为基础,采用数理统计和模糊统计方法对经验判断法获得的信息统计分析,从而确定权重集。
层次分析法是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。该方法将定量分析与定性分析结合起来,用决策者的经验,判断各衡量目标能否实现的标准之间的相对重要程度,并合理地给出每个决策方案的每个标准的权数,利用权数求出各方案的优劣次序,比较有效地应用于那些难以完全用定量方法解决的课题。
一、基本原理
层次分析法根据问题的性质和要达到的总目标,将问题分解为不同的组成因素,并按照因素问的相互关联影响以及隶属关系将因素按不同层次聚集组合,形成一个多层次的分析结构模型,从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。
二、主要内容与基本步骤
1.建立层次结构模型
将问题中包含的因素划分为不同层次,用框图形式说明层次的阶梯结构和因素的从属关系。
应用层次分析法研究问题时,首先要对问题有明确的认识,弄清问题的范围、所包含的因素、因素间的相互关联、隶属关系,最终要解决的问题。根据对问题的初步分析,将问题包含的因素按照是否共有某些特性聚集成组,并把它们之间的共有特性看作是系统的新层次中的一些因素,而这些因素本身也按照另外一组特性被组合,形成另外的更高层次的因素,直到最终形成单一的最高因素,也就是我们决策的目标。这样就可以构成由最高层、若干中间层和最低层排列组成的层次分析结构模型。对于决策问题,通常可以划分为下面几个层次:
最高层,表示解决问题的目的,即层次分析要达到的总目标,即选择合理的供应商。
中间层,表示采取某种措施、政策、方案等来实现预定总目标所涉及的中间环节,一般又可以分为策略层、约束层、准则层等。衡量目标能否实现的标准,即用评标的标准综合考察各供应商的实力,如产品质量,资历、经济实力、社会信誉等。
最低层,表示要选用的解决问题的各种措施、政策、方案等。在这里就是指各供应商。层次分析法所要解决的问题是关于最低层对最高层的相对权重问题,按此相对权重可以在不同的方案中做出选择或形成选择方案的原则。
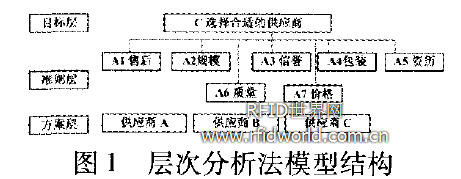
根据以上层次分析法理论,设计物料管理系统层次分析图如下所示。
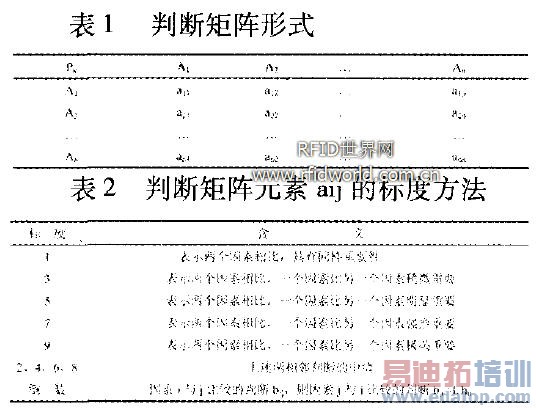
任何系统分析都以一定的信息为基础,层次分析法的信息基础主要是人们对于每一层次中各因素相对重要性的判断。这些判断通过引入合适的标度,用数值表示出来,形成判断短阵。判断矩阵表示针对上一层次某个元素,本层次与其有关因素的相对重要性的比较。若A层次的上一层次P的因素P 与A层次中的A1,A2,...,An有联系,则判断矩阵形式如表2表示。判断矩阵的元素aij用萨蒂的1—9标度方法给出(如表1所示)。
相应于判断矩阵最大特征根λmax的特征向量,经过归一化(使向量中各元素之和= 1)后记为w。w 的元素为同一层次因素对于上一层次某因素相对重要性的排序权值,这一过程称为层次单排序。
根据Perron定理的推论:n阶正互反矩阵A=(aij)m(n的最大特征根(max(n,当且仅当A为一致时(max=n,当A不一致时,(max(n。在层次分析中,我们允许A存在一定的不一致性,但是A的不一致必须控制在一定的允许范围内,(max 比n大的越多,A的不一致程度越高,(max对应的权向量w各分量反映出来的权重与实际权重的偏差可能会越大,因此Saaty首先提出用随机性指标:对固定的n,随机地构造出正互反矩阵A(,其中aij(i<j)随机地取自1/9,...,1/2,1,2,... 9,用充分大的子样(如1000个子样)得到A的最大特征值的平均值(max,定义随机性指标CI(如下式),用CR判断正互反矩阵的一致性可否接受。
平均随机一致性指标RI的值如表3所示。
表3 平均随机一致性指标RI的值
4.层次总排序
计算同一层次所有因素对于最高层(总目标)相对重要性的权值,称为层次总排序。这一过程是最高层次到最低层次进行的。若上一层次A包含m个因素A1,A2,......,Am,下一层次B包含B1,B2,......,Bn ,它们对于因素A 的层次单排序权值分别为b1j,b2j,......,b nj,(当Bk与Aj无联系时,bkj=0),则B层次总排序权值由表4给出。
表4 B层次总排序权值计算法
5.一致性检验
为了评价层次总排序的计算结果的一致性,类似于层次单排序,也需要进行一致性检验。为此,需要
分别记算下列指标:
同样,当CR<0.10时,则认为层次总排序的计算结果具有令人满意的一致性;否则,就需要对本层次的各判断矩阵进行调整,从而使层次总排序具有令人满意的一致性。
层次分析法是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。该方法将定量分析与定性分析结合起来,用决策者的经验,判断各衡量目标能否实现的标准之间的相对重要程度,并合理地给出每个决策方案的每个标准的权数,利用权数求出各方案的优劣次序,比较有效地应用于那些难以完全用定量方法解决的课题。
一、基本原理
层次分析法根据问题的性质和要达到的总目标,将问题分解为不同的组成因素,并按照因素问的相互关联影响以及隶属关系将因素按不同层次聚集组合,形成一个多层次的分析结构模型,从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。
二、主要内容与基本步骤
1.建立层次结构模型
将问题中包含的因素划分为不同层次,用框图形式说明层次的阶梯结构和因素的从属关系。
应用层次分析法研究问题时,首先要对问题有明确的认识,弄清问题的范围、所包含的因素、因素间的相互关联、隶属关系,最终要解决的问题。根据对问题的初步分析,将问题包含的因素按照是否共有某些特性聚集成组,并把它们之间的共有特性看作是系统的新层次中的一些因素,而这些因素本身也按照另外一组特性被组合,形成另外的更高层次的因素,直到最终形成单一的最高因素,也就是我们决策的目标。这样就可以构成由最高层、若干中间层和最低层排列组成的层次分析结构模型。对于决策问题,通常可以划分为下面几个层次:
最高层,表示解决问题的目的,即层次分析要达到的总目标,即选择合理的供应商。
中间层,表示采取某种措施、政策、方案等来实现预定总目标所涉及的中间环节,一般又可以分为策略层、约束层、准则层等。衡量目标能否实现的标准,即用评标的标准综合考察各供应商的实力,如产品质量,资历、经济实力、社会信誉等。
最低层,表示要选用的解决问题的各种措施、政策、方案等。在这里就是指各供应商。层次分析法所要解决的问题是关于最低层对最高层的相对权重问题,按此相对权重可以在不同的方案中做出选择或形成选择方案的原则。
根据以上层次分析法理论,设计物料管理系统层次分析图如下所示。
任何系统分析都以一定的信息为基础,层次分析法的信息基础主要是人们对于每一层次中各因素相对重要性的判断。这些判断通过引入合适的标度,用数值表示出来,形成判断短阵。判断矩阵表示针对上一层次某个元素,本层次与其有关因素的相对重要性的比较。若A层次的上一层次P的因素P 与A层次中的A1,A2,...,An有联系,则判断矩阵形式如表2表示。判断矩阵的元素aij用萨蒂的1—9标度方法给出(如表1所示)。
相应于判断矩阵最大特征根λmax的特征向量,经过归一化(使向量中各元素之和= 1)后记为w。w 的元素为同一层次因素对于上一层次某因素相对重要性的排序权值,这一过程称为层次单排序。
根据Perron定理的推论:n阶正互反矩阵A=(aij)m(n的最大特征根(max(n,当且仅当A为一致时(max=n,当A不一致时,(max(n。在层次分析中,我们允许A存在一定的不一致性,但是A的不一致必须控制在一定的允许范围内,(max 比n大的越多,A的不一致程度越高,(max对应的权向量w各分量反映出来的权重与实际权重的偏差可能会越大,因此Saaty首先提出用随机性指标:对固定的n,随机地构造出正互反矩阵A(,其中aij(i<j)随机地取自1/9,...,1/2,1,2,... 9,用充分大的子样(如1000个子样)得到A的最大特征值的平均值(max,定义随机性指标CI(如下式),用CR判断正互反矩阵的一致性可否接受。
平均随机一致性指标RI的值如表3所示。
表3 平均随机一致性指标RI的值

4.层次总排序
计算同一层次所有因素对于最高层(总目标)相对重要性的权值,称为层次总排序。这一过程是最高层次到最低层次进行的。若上一层次A包含m个因素A1,A2,......,Am,下一层次B包含B1,B2,......,Bn ,它们对于因素A 的层次单排序权值分别为b1j,b2j,......,b nj,(当Bk与Aj无联系时,bkj=0),则B层次总排序权值由表4给出。
表4 B层次总排序权值计算法

5.一致性检验
为了评价层次总排序的计算结果的一致性,类似于层次单排序,也需要进行一致性检验。为此,需要
分别记算下列指标:

同样,当CR<0.10时,则认为层次总排序的计算结果具有令人满意的一致性;否则,就需要对本层次的各判断矩阵进行调整,从而使层次总排序具有令人满意的一致性。


