RFID基带信号频率偏差检测

1 引言

　　无线射频识别技术（Radio Frequency IdenTIficATIon，RFID），是一种利用无线射频方式在阅读器和标签之间进行非接触双向数据传输，以达到目标识别和数据交换目的的技术。典型的RFID系统是由电子标签、读写器和后台管理计算机3部分组成。RFID的性能受到产品材质、传输带速率、交互方式、 标签粘贴位置等多种因素的影响。所以就需要对RFID的性能进行测试，保证RFID的产品质量。

　　RFID 的基带频率偏差就是其中一项很重要的内容。电子标签返回的高频信号被天线接收后，经过放大、解调等步骤后得到的信号称为基带信号。对运用微计算机测量基带信号的频率测量进行了探讨。对于基带信号的解码方法主要有二元序贯检测和相关检测，然而对于如何确定基带信号的频率偏差相关文献较少。

　　2 基带信号特点

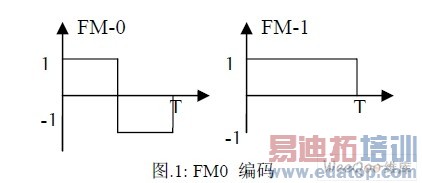
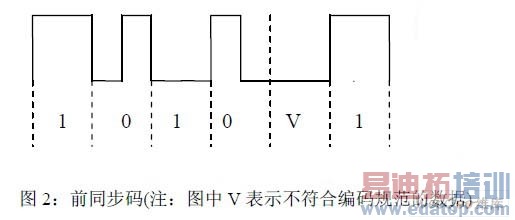
　　与其他无线通信系统相比，RFID 有其自身的特点。首先基带数据采用FM0 编码，如图1 所示。数据速率可以在40k~640kbps 连续变化且最大允许频偏为22%。但是在不同数据速率和不同温度下，RFID 标准对于频偏有不同要求。其次，由于标签到读写器的数据必须以图2 所示的前同步码开始，而前同步码只有6 个数据，数据长度过短而无法实现频率同步。上述特点都给频率偏差检测设计带来了相当大的困难。

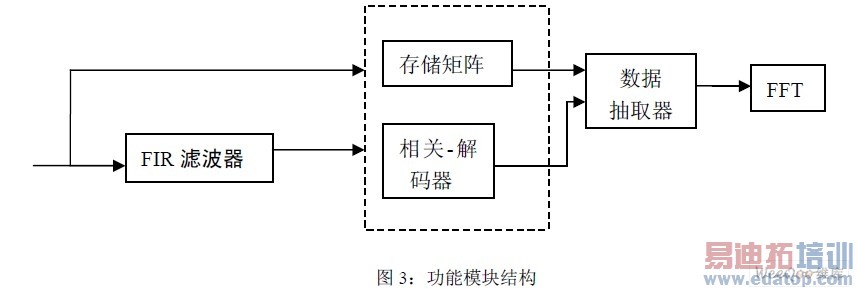
       3 频偏测量方法

　　本文总体思路如下：①.首先对采样信号进行FIR 滤波②.通过相关运算捕捉前同步码,解码数据，并预估频偏的大致范围。③对于滤波前的基带采样数据进行适当抽取，构造波形。④通过FFT 确定频偏。功能模块见图3。为了方便讨论，假设过采样速率为8；高电平用1 表示，低电平用-1 表示；S 表示采样点序列；D 表示FM0 解码序列；S[i:j]≡1 表示序列S 中从i 到j 的数据全为高电平;S[i:j]≡-1 表示序列S 中从i 到j 的数据全为低电平。用L 加下标表示序列的长度。

      3.1 FIR 滤波器

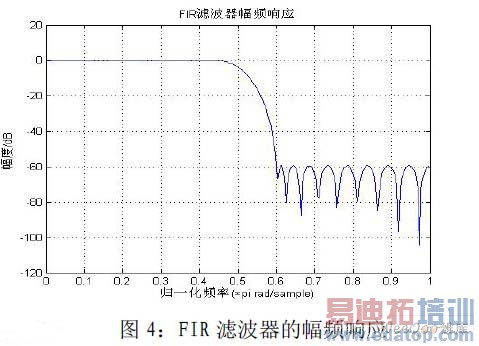
　　介绍了几种频率检测的方法，文献中认为IIR 滤波器是一个非常适当且高效的滤波器，但是采用FIR 滤波器。考虑到IIR 滤波器的自激振荡问题，采用FIR 滤波器。其幅频响应如图4 所示。

       3.2 相关-解码器

　　由于RFID基带信号通常采用FM0编码。且前一数据和后一数据之间必然存在电平跳变。即如果前一数据以高电平结束，下一数据则以低电平开始；如果前一数据以低电平结束，下一数据则以高电平开始。通过前同步码的相关(公式(1))完成数据起点的捕捉，考虑FM0编码的正交性（公式(2)）完成数据解码。设求得的数据起点为k，结束点为e。解码后数据序列为D，假设D 的长度为LD。由前同步码的相关与门限的比较得到频偏范围R1。由k、e 得到预估频偏R2 ，其中R2 使得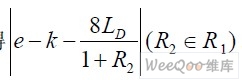最小。

　　3.3 存储矩阵

　　存储矩阵存储不同频率偏差o 下的基带采样点数序列To 和采样数据序列S,采样点数序列To 是由频偏为o%时的基带FM0 全0 编码通过ADC 得到。

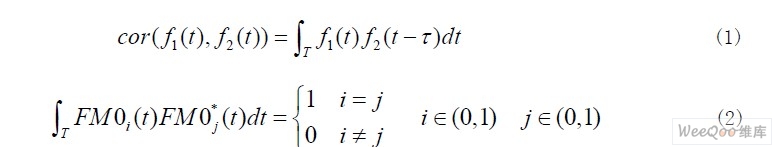
       3.4 数据抽取器

　　对于采样数据S,如果有S[PO[i]:PO[i+1]-1]≡1, S[PO[i+1]: PO[i+2]-1]≡-1(PO 序列构造算法附后)。可对序列S 进行如下抽取：

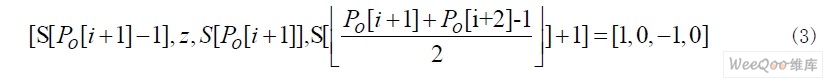
       对于其余的采样数据S,如果有S[P[i]: P[i+1]-1]≡-1, S[P[i+1]: P[i+2]-1] ≡1。可对序列L 进行如下抽取：

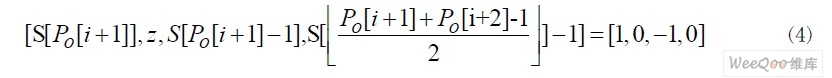
       注：z 表示用S 中的噪声数据进行补齐。

　　考虑前同步码以高电平结束，则有初始电平 e=-1,设i=1。由此得到序列F 的抽取算法：

　　A. If(i<=PO L -2)转B, 否则结束。

　　B. 如果 e=1，根据Po[i]、Po [i+1]、Po [i+2]参考公式(3)构造a。如果e=-1，根据Po[i]、Po[i+1]、Po[i+2]参考公式(4)构造f。转C

　　C. F=[F f], i=i+1，e= -e。转A。

　　注：F=[F f],,表示将序列f 添加在F 的后面，构成新的序列F。通过上述思路，将基带采样信号抽取为余弦信号的4 倍抽样。对于不同频率偏差o 下的Po 序列，可由序列To、解码序列 D 及数据起点k 得到。假设序列D 的第一个数据D1=1，Po[1]=k, Po[2]= Po[1]+To[1]+To[2]；如果D1=0，则有Po[1]=k，Po[2]= Po[1]+To[1]，Po[3]=Po[2]+To[2]。由此得到Po 序列构造算法：

　　A. P[1]=k，i=2，j=1。

　　B. If(j> LD)结束。如果D[j]==1，转C,否则转D。

　　C. Po[i]=Po[i-1]+To[2j-1]+To[2j],i=i+1。转E。

　　D. Po[i]=Po[i-1]+To[2j-1], Po[i+1]=Po[i]+To[2j],i=i+2。转E

　　E. j=j+1 转B。

　　3.4 频谱分析

　　假设真实频偏为r,实际数据起点为a。以a-1、a、a+1 为数据起点，以r-1%、r、r+1%为参考频偏，其抽取序列的频谱如图5 所示。频谱计算见公式(5)，其中FFT(F)表示对序列F 进行点FFT 变换。

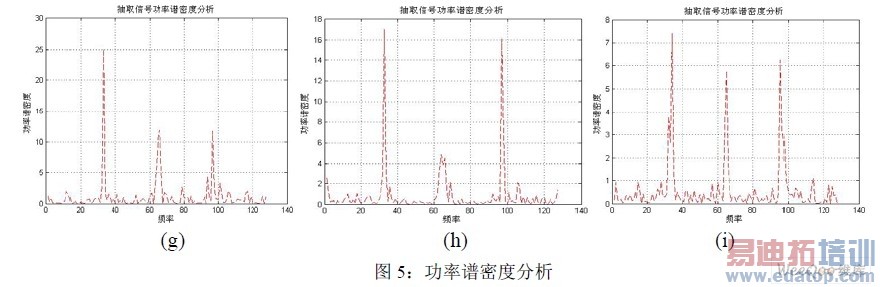
       由上述频谱结果可知，频谱存在如下特点：①.频谱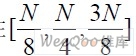在处存在峰值。即序列F由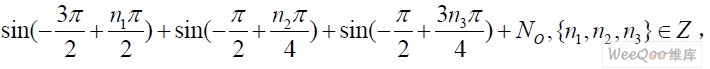No为环境噪声; ②.以 r 为参考频偏、a 为参考起点构造序列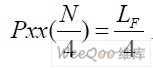，且平均噪声密度∂最小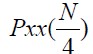，计算见公式(6)，定义见公式（7）；③如果参考频率不等于真实频率，则在点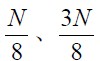处功率谱密度较大且∂较大。可以根据上述特点进行频偏确定。

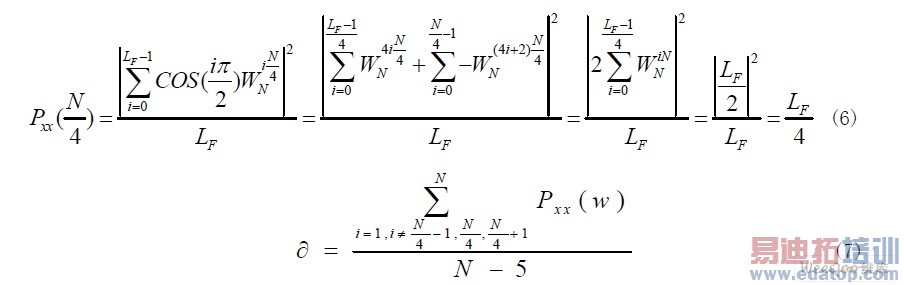
       考虑谱线分裂现象，用代替理论上的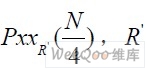为参考频偏，判决门限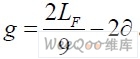构造波形的运算量为加法运算，且复杂度为o(LD),而FFT 乘法运算量为o(NLogN),且有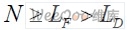。所以运算量主要由FFT 决定。由以上分析，得到思路如下：

　　A. 以R2 为参考频偏、k为参考起点，构造波形，进行功率谱密度分析。如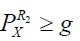确定R2 为频偏；否则转B。此时运算量1 个FFT。

　　B. R2 为参考频偏、k-1、k+1 为参考起始点，构造波形，进行功率谱密度分析，如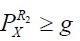确定R2为频偏；否则转C。此时运算量3个FFT。

      4 仿真结果及结论

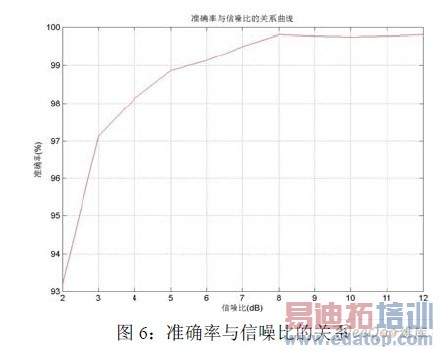
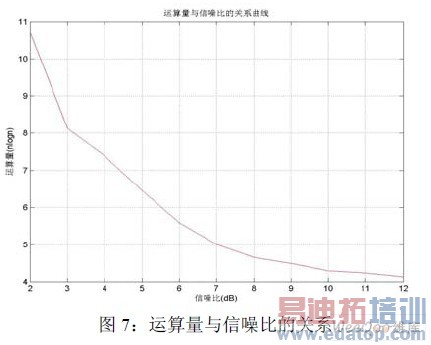
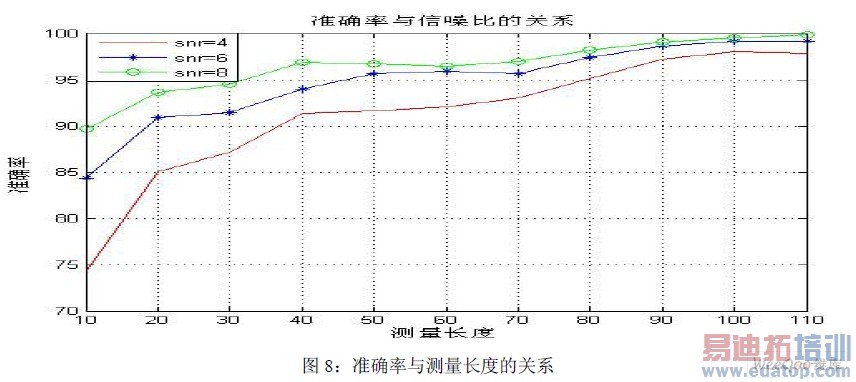
　　以加性高斯白噪声为噪声坏境，得到仿真结果如图所示。图6 为测量准确率与信噪比的关系，图7 为运算量与信噪比的关系。测量长度为110 个FM0 码，运算量的单位为一个FFT 运算即nlogn 次乘法运算。图8 为不同信噪比下准确率与测量长度的关系。本文通过对RFID 基带信号频率偏差检测的为研究对象。对于RFID 的基带采样信号，首先低通滤波，通过相关运算捕捉数据起点并完成数据解码；从而确定频偏的大致范围；最后基带采样信号的适当抽取，构造波形进行FFT 变换确定频偏。根据仿真结果，在测量长度大于90 时，测量结果可以达到99%以上，SNR>6dB 时，运算量大概在(4~6)个FFT 运算。如何降低运算量并减少测量长度仍然是一个值得研究的方向。