改进Monte Carlo定位算法用于RFID标签的室内定位

引言

随着RFID的日臻完善，对射频标签进行 定位 就成为一项重要课题^[1]。利用标签对物体的唯一标识特性，可以依据读写器与安装在物体上的标签之间的信号到达时间延迟（TOA）来估计标签与读写器之间的距离。在室内环境中，由于存在较为严重的非视距（NLOS）传播情况，使得基于TOA的测量值发生很大偏差，从而不能正确反映标签与读写器之间的距离。对于TOA测量值中NLOS误差的抑制和消除，在各种文献中已提出了多种方法^[２-3]。但基于TOA的 定位 算法往往需要三支以上的天线覆盖同一区域。需要的天线数越多，系统成本越高。当室内的阻挡物较多时，在读写器的工作范围内，三台读写器中只要有一台读写器接收不到标签信号，基于TOA的 定位 算法就无法对标签进行 定位 。然而，Monte Carlo 定位 算法^[4]仍然能保持对标签的跟踪。

本文改进了Monte Carlo 定位 算法，将其用于室内射频标签的 定位 ，分析了天线极化失配对改进的Monte Carlo 定位 算法的影响。

1 RFID 定位 原理

在第k-1时刻，通过预测模型预测k时刻标签可能会出现的位置；在第k时刻，测得标签与读写器之间的距离，通过测量模型计算出标签的位置。其中，所用到的读写器天线覆盖模型、预测模型、测量模型分别由1.1-1.3小节给出。

1.1 天线覆盖模型

在具体应用中，为节约成本，希望使用尽可能少的读写器天线来实现室内的覆盖。因此，只有当获得了天线的覆盖模型时，才有可能更加精确的指导读写器天线的部署。假设室内的长宽高为6*6*3 ，电波频率为915MHz，读写器的发射功率为1w。读写器天线为半波振子，水平安装在天花板上距地面2.5m处。图1为当不考虑天花板对天线的影响时，读写器天线在地面的覆盖范围图。其中，A、B、C为功率电平值，即标签被识读的最小功率电平。标签的最小功率电平决定了读写器天线的覆盖范围，对读写器天线的部署意义重大。本文采用最小功率电平A所对应的读写器天线的覆盖范围来指导读写器天线的部署，则读写器天线的安装位置为(1.5,1.5)(1.5,4.5)(4.5,1.5)(4.5,4.5)(3,1)(3,5)(1,3)(5,3)。

图1 读写器天线在地面的覆盖范围

（直线表示天线放置的方向）

1.2 预测模型^[4]

在第k-1时刻，通过预测模型预测第k时刻标签可能会出现的位置，即计算采样点的位置。假设室内噪声为高斯噪声，采用高斯分布的预测模型为：

2 Monte Carlo改进 定位 算法

在阐述贝叶斯滤波原理的基础上，针对传统Monte Carlo 定位 算法存在的缺陷，提出了用于室内射频标签 定位 的改进Monte Carlo 定位 算法。

2.1 贝叶斯滤波^[4]

2.2 改进的Monte Carlo 定位 算法流程

3 模拟与仿真

假设标签的运动轨迹为:(3,0)(3,1)(3,1.8)(3.8,1.8)(5,1.8)(5,2.8)(5,3.8)(5,5)(4.5,4.5)(4,5)

(3.2,5)(2,5)(1,5)(1,4.1)(1,3.1)(1,2.3)(1,1.6)(1,0.7)。

3.1 极化失配对Monte Carlo改进 定位 算法性能的影响

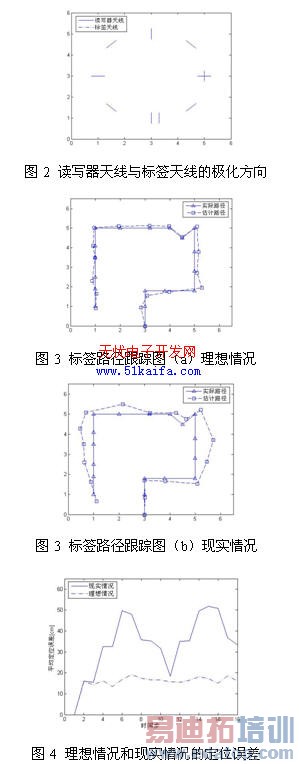
天线的极化方向是天线辐射的电磁场的电场方向。接收天线的极化方式只有同被接收的电磁波极化形式相一致时，才能有效地接收到信号，否则将使接收信号质量变差，甚至完全接收不到信号，这种现象称为极化失配。图2为标签天线与读写器天线的极化方向图。图3和图4为理想情况（标签与读写器天线的极化方向时时对准）与现实情况（本文中RFID室内 定位 系统的天线极化失配）Monte Carlo改进 定位 算法的标签跟踪和 定位 误差图。可以看出，当标签天线的极化方向与读写器天线的极化方向时时一致时，Monte Carlo改进 定位 算法的 定位 误差较小；当考虑标签与读写器天线之间的极化失配时，Monte Carlo改进 定位 算法的 定位 误差较大，且 定位 误差随标签与读写器天线之间极化方向的夹角的增大而增大。

4 结论

改进的Monte Carlo 定位 算法能够适应动态环境， 定位 的稳定性好。此外，改进的Monte Carlo 定位 算法受天线极化失配的影响较大， 定位 误差随标签与读写器天线之间极化方向的夹角的增大而增大。

本文作者创新点:改进了Monte Carlo 定位 算法，将其用于室内射频标签的 定位 ，分析了天线极化失配对改进的Monte Carlo 定位 算法的影响。

参考文献:

[1] 吴永祥，射频识别（RFID）技术研究现状及发展展望[J]．微计算机信息，2006，11-2: 234-236。

[2] M. Wylie, J. Holtzman, The non-line of sight problem in mobile location estimation [C], IEEE International Conference on Universal Personal Communications, pp.827-831, 1996.

[3] P. Chen, A non-line-of-sight error mitigation algorithm in location estimation [C], Wireless Communications and Networking Conference, pp.316-320, 1999.

[4] D. Jourdan, J. Deyst and M. Win, Monte-Carlo localization in dense multipath environments using UWB ranging [C], In Proceedings of IEEE International Conference on Ultra-Wideband, Zurich, pp.314–319, September 2005.