- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
多晶微波铁氧体材料中的铁磁弛豫过程研究
录入:edatop.com 点击:
多晶微波铁氧体材料中的铁磁弛豫过程研究
韩志全
(中国西南应用磁学研究所,四川绵阳 621000)
摘 要:基于晶粒表层自旋波共振模型对有效线宽行为的成功解释,提出在多晶中存在一个由晶粒表层自旋波系统到晶格的弛豫过程,这一弛豫过程在非共振区是微波能量损耗的主渠道。
关键词:微波铁氧体;损耗;铁磁共振;有效线宽
关键词:微波铁氧体;损耗;铁磁共振;有效线宽
1 前言
随着石榴石等微波铁氧体材料的问世和旋磁器件的发展,早在六十年代初,材料中的微波能量损耗机制就成为了研究的热点。Lax和Button[1], Sparks[2] 和Patton[3]等都先后就此作过精辟的论述。他们的铁磁弛豫理论,详细研究了由微波场激发的磁矩一致进动是如何将能量损耗掉的各种弛豫过程。这些理论成功地解释了单晶材料的各种微波特性,然而,对多晶却只能就有效线宽DHeff在共振区的行为作出描述,不能说明非共振DHeff的较高数值及△Heff与晶粒尺寸相关等实验事实 [4~7]。最近,晶粒表层自旋波共振激发模型[8]对这些问题作出了圆满的解释。本文旨在基于这一模型进一步探讨多晶材料中的特殊能量弛豫过程。
2 铁磁弛豫理论
2.1 弛豫时间τ、阻尼系数α、线宽△H、有效线宽△Heff
众所周知,磁化强度进动方程中的阻尼系数α、弛豫时间τ与铁磁共振线宽DH之间的关系为[2]:
△H=2αω/γ=2/γτ (1)
只要测得了DH便可得知阻尼系数a、弛豫时间t。
上式是在假定阻尼系数α和旋磁比γ与内稳恒磁场Hi无关的情况下得出的。在拟合多晶的 (Hi)实验数据时[4,7]发现,对大多数多晶铁氧体不得不引入为Hi的函数的α和γ,令有效线宽
(Hi)实验数据时[4,7]发现,对大多数多晶铁氧体不得不引入为Hi的函数的α和γ,令有效线宽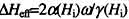 ,则它与内禀磁化率
,则它与内禀磁化率 的关系为[4,7,9] :
的关系为[4,7,9] :
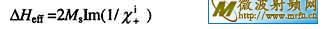
其中Im(1/x+)表示1/x+的虚部。实际上,有效线宽DHeff比线宽DH更能直接地反映多晶材料的损耗。
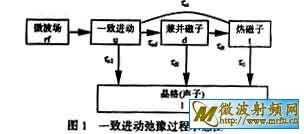
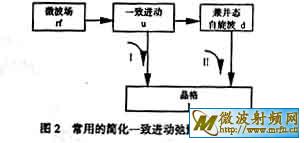
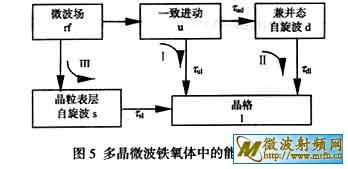
2.2 弛豫过程 弛豫时间t的长短是损耗大小的度量,t取决于弛豫过程。所有过程的能量和动量都必须守恒。Sparks给出的弛豫过程如图1所示[2]。图中tud是一致进动(k=0的磁子)到能量相同的(兼并态)自旋波的弛豫过程,为双磁子散射过程。即,在k=0的磁子湮没的同时k10的磁子产生,它们的动量差由不均匀场来补足。tul, tdl和t tl是磁子到声子(通过自旋-轨道,轨道-晶格耦合)的弛豫过程。tdt和tut是三磁子过程,即两个磁子合并产生第三个磁子或一个入射磁子分裂成两个磁子的过程, 它们来自于磁偶极矩长程相互作用,可用来解释超纯、高度抛光YIG单晶的线宽。由于三磁子以上的高阶过程一般只有在一致进动被高度激发(有高输入功率)的情况下,才具有不可忽略的效应,通常将图1简化成图2中的两个通道I和II [9]。
2.3 损耗主渠道 在通道I和II中, 通道II的的弛豫时间tud+tdl最短。因而, 由一致进动经过兼并自旋波到晶格的弛豫过程是微波能量损耗的主渠道, 几率最大。实验表明tdl比tud要短些, 因此, 通道II的畅通与否主要取决于一致进动到兼并自旋波的弛豫时间tud。由于能量要守恒, tud与自旋波谱有关;因动量要守恒,tud还与样品中存在的不均匀性有关, 包括气孔、晶界、晶粒表层、晶粒取向、杂质、表面凹坑、磁有序等。
2.4 铁磁弛豫理论与实验 考虑了气孔周围的杂散场和晶粒无规取向所带来的磁不均匀性,Patton用双磁子散射理论对共振区DHeff作出了定量上较为一致的描述[4~6]。在非共振区特别是高场区,理论认为由于在自旋波簇之外不存在兼并态自旋波模式也就不存在双磁子散射机制,一致进动的弛豫率非常低,接近于零,这时的DHeff应该非常小(相当于完美单晶的DH),并与晶粒尺寸、气孔率等磁不均匀性无关。但实验结果并非如此[4~7]。
随着石榴石等微波铁氧体材料的问世和旋磁器件的发展,早在六十年代初,材料中的微波能量损耗机制就成为了研究的热点。Lax和Button[1], Sparks[2] 和Patton[3]等都先后就此作过精辟的论述。他们的铁磁弛豫理论,详细研究了由微波场激发的磁矩一致进动是如何将能量损耗掉的各种弛豫过程。这些理论成功地解释了单晶材料的各种微波特性,然而,对多晶却只能就有效线宽DHeff在共振区的行为作出描述,不能说明非共振DHeff的较高数值及△Heff与晶粒尺寸相关等实验事实 [4~7]。最近,晶粒表层自旋波共振激发模型[8]对这些问题作出了圆满的解释。本文旨在基于这一模型进一步探讨多晶材料中的特殊能量弛豫过程。
2 铁磁弛豫理论
2.1 弛豫时间τ、阻尼系数α、线宽△H、有效线宽△Heff
众所周知,磁化强度进动方程中的阻尼系数α、弛豫时间τ与铁磁共振线宽DH之间的关系为[2]:
△H=2αω/γ=2/γτ (1)
只要测得了DH便可得知阻尼系数a、弛豫时间t。
上式是在假定阻尼系数α和旋磁比γ与内稳恒磁场Hi无关的情况下得出的。在拟合多晶的
其中Im(1/x+)表示1/x+的虚部。实际上,有效线宽DHeff比线宽DH更能直接地反映多晶材料的损耗。
2.2 弛豫过程 弛豫时间t的长短是损耗大小的度量,t取决于弛豫过程。所有过程的能量和动量都必须守恒。Sparks给出的弛豫过程如图1所示[2]。图中tud是一致进动(k=0的磁子)到能量相同的(兼并态)自旋波的弛豫过程,为双磁子散射过程。即,在k=0的磁子湮没的同时k10的磁子产生,它们的动量差由不均匀场来补足。tul, tdl和t tl是磁子到声子(通过自旋-轨道,轨道-晶格耦合)的弛豫过程。tdt和tut是三磁子过程,即两个磁子合并产生第三个磁子或一个入射磁子分裂成两个磁子的过程, 它们来自于磁偶极矩长程相互作用,可用来解释超纯、高度抛光YIG单晶的线宽。由于三磁子以上的高阶过程一般只有在一致进动被高度激发(有高输入功率)的情况下,才具有不可忽略的效应,通常将图1简化成图2中的两个通道I和II [9]。
2.3 损耗主渠道 在通道I和II中, 通道II的的弛豫时间tud+tdl最短。因而, 由一致进动经过兼并自旋波到晶格的弛豫过程是微波能量损耗的主渠道, 几率最大。实验表明tdl比tud要短些, 因此, 通道II的畅通与否主要取决于一致进动到兼并自旋波的弛豫时间tud。由于能量要守恒, tud与自旋波谱有关;因动量要守恒,tud还与样品中存在的不均匀性有关, 包括气孔、晶界、晶粒表层、晶粒取向、杂质、表面凹坑、磁有序等。
2.4 铁磁弛豫理论与实验 考虑了气孔周围的杂散场和晶粒无规取向所带来的磁不均匀性,Patton用双磁子散射理论对共振区DHeff作出了定量上较为一致的描述[4~6]。在非共振区特别是高场区,理论认为由于在自旋波簇之外不存在兼并态自旋波模式也就不存在双磁子散射机制,一致进动的弛豫率非常低,接近于零,这时的DHeff应该非常小(相当于完美单晶的DH),并与晶粒尺寸、气孔率等磁不均匀性无关。但实验结果并非如此[4~7]。

3 晶粒表层自旋波共振模型 为了寻求非共振DHeff的来源,我们在文献[8]中考虑了晶粒表层中不同于内部的磁晶各向异性常数Ks(在金属永磁材料中曾用的具有不同于内部的交换系数A′和各向异性常数K′的晶粒表层模型及有不同各向异性常数K(z) 的晶粒表层模型[10-14] 来说明矫顽力行为)及各向异性场Hs(=2Ks/Ms),它是由杂质和应力引起的。计入Hs,由晶粒表层磁化强度Ms的进动方程出发,解出了晶粒表层自旋波谱:
其中 是晶粒表层中的内场(图3),
是晶粒表层中的内场(图3),
 是沿样品Z轴方向(外加稳恒磁场方向)上的退磁因子,Ms是材料的饱和磁化强度,θ是晶粒表层法线方向
是沿样品Z轴方向(外加稳恒磁场方向)上的退磁因子,Ms是材料的饱和磁化强度,θ是晶粒表层法线方向 轴与外加稳恒磁场方向Z轴的夹角,D=2A/Ms,A是交换系数,θk是自旋波波矢k方向(即表层法线
轴与外加稳恒磁场方向Z轴的夹角,D=2A/Ms,A是交换系数,θk是自旋波波矢k方向(即表层法线 轴)与表层内场
轴)与表层内场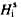 的方向z轴的夹角, 实际上 θk=θm(θm为
的方向z轴的夹角, 实际上 θk=θm(θm为 的方向z与
的方向z与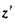 轴的夹角),k=2nπ/L,n=0,1,2,3,….。取θk=p/2,θ=p/2 和θk=0, θ=0便可分别获得(3)式的上下限:
轴的夹角),k=2nπ/L,n=0,1,2,3,….。取θk=p/2,θ=p/2 和θk=0, θ=0便可分别获得(3)式的上下限:
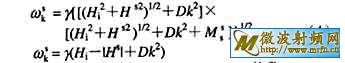
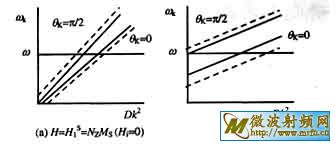
它们所构成的自旋波簇要比晶粒内部的[4~7]宽(图4)。这表明低场和高场虽是晶粒内部的非共振区,却是晶粒表层的共振区。公式(3)~(5)及图4较以前发表过的[15,16]略有不同,这是因为文献[8]在解进动方程时在处理方法上作了改进(取消了θ≈θm的假设、多了个变量θ)。我们认为本文即文献[8]的更为恰当。
4 非共振有效线宽的来源
4.1 多晶的内禀磁化率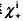 和非共振有效线宽△Heff
和非共振有效线宽△Heff
根据在YIG薄膜铁磁共振谱中观测到的表面模和体模分立谱随还原时间变化所证实的独立共振行为[17~19],可以假设多晶材料的内禀磁化率 实际上是晶粒表面的和晶粒内部的各自独立共振行为的总和。可记为:

其中f (θ,H)是在共振晶粒表层比例系数,S是场移,它说明非共振△Heff来源于晶粒表层的自旋波共振激发,即晶粒表层的自旋波共振损耗 。
。
4.2 晶粒表层自旋波共振模型与实验的一致性[8] (7)式中的Vs与d及晶粒表层厚度L的关系已知为Vs=4L/d, 则

实验给出n=1~0.5,m=1[4~7]。由估算值2L" 0.4mm[8],推知d=1, 3 ,10 mm时 Vs"40%, 13% , 4% 。因此,(7)式和(8)式成功地解释了△Heff远大于单晶线宽的较高数值、DHeff与晶粒尺寸d及气孔率p的关系。
预期在高场区存在DHeff的截止场Hcut,这是因为随磁场的增大自旋波簇上移,当磁场增大到w 出了晶粒表层自旋波簇时DHeff应有的明显下降,实验与之相符[7]。由高场Hcut数据,据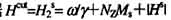 估算出了气孔率p=2%和5%的NiZn铁氧体的Hs分别为-750 Oe和-1800 Oe, YIG的Hs为-900 Oe[8]。
估算出了气孔率p=2%和5%的NiZn铁氧体的Hs分别为-750 Oe和-1800 Oe, YIG的Hs为-900 Oe[8]。
(7)式中DHeff与Ms的反比关系与我们的实验结果 较为一致[8]。由(7)式中的温度的减函数
较为一致[8]。由(7)式中的温度的减函数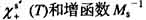 (T)相互补偿的结果可说明DHeff温度曲线的特性[6]:T <250 K平缓,T >250 K下降。
(T)相互补偿的结果可说明DHeff温度曲线的特性[6]:T <250 K平缓,T >250 K下降。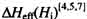 和场移S(Hi)随磁场的变化曲线等也均可由(7)式给出合理解释[8]。
和场移S(Hi)随磁场的变化曲线等也均可由(7)式给出合理解释[8]。
5 能量损耗渠道
由Lax, Sparks, Patton等人建立起来的铁磁弛豫理论的共同特点是:微波能量,不论通过什么途径,都经由一致进动最终传递给晶格,以热能的形式耗散掉。
(7)式在解释DHeff远大于单晶线宽的较高数值、DHeff与晶粒尺寸及气孔率的关系、DHeff的温度特性、DHeff与Ms的反比关系、高场DHeff的截止场以及DHeff(Hi)、S(Hi)曲线等方面的成功[8], 表明了晶粒表层自旋波共振模型是可取的。这说明,在多晶铁氧体材料中微波磁场不仅可以激发一致进动,也可以激发晶粒表层中的自旋波共振。即,实际上还另外存在着一个微波能量经过晶粒表层自旋波系统到达晶格的弛豫过程,见图5中的通道III。特别是在非共振区,由于不存在与一致进动具有相同能量的兼并态自旋波模式,则不可能发生双磁子散射,通道II不通,这时微波能量经过晶粒表层自旋波系统到晶格的弛豫过程(通道III)就成为了能量损耗的主渠道。在细晶粒样品中,由于晶粒表层所占的体积分数较大(d=1 mm时估算值 Vs"40%),这一弛豫机制尤其不可忽略。
其中
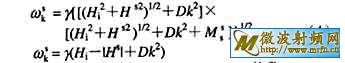
它们所构成的自旋波簇要比晶粒内部的[4~7]宽(图4)。这表明低场和高场虽是晶粒内部的非共振区,却是晶粒表层的共振区。公式(3)~(5)及图4较以前发表过的[15,16]略有不同,这是因为文献[8]在解进动方程时在处理方法上作了改进(取消了θ≈θm的假设、多了个变量θ)。我们认为本文即文献[8]的更为恰当。
4 非共振有效线宽的来源
4.1 多晶的内禀磁化率
根据在YIG薄膜铁磁共振谱中观测到的表面模和体模分立谱随还原时间变化所证实的独立共振行为[17~19],可以假设多晶材料的内禀磁化率 实际上是晶粒表面的和晶粒内部的各自独立共振行为的总和。可记为:

其中f (θ,H)是在共振晶粒表层比例系数,S是场移,它说明非共振△Heff来源于晶粒表层的自旋波共振激发,即晶粒表层的自旋波共振损耗
4.2 晶粒表层自旋波共振模型与实验的一致性[8] (7)式中的Vs与d及晶粒表层厚度L的关系已知为Vs=4L/d, 则
实验给出n=1~0.5,m=1[4~7]。由估算值2L" 0.4mm[8],推知d=1, 3 ,10 mm时 Vs"40%, 13% , 4% 。因此,(7)式和(8)式成功地解释了△Heff远大于单晶线宽的较高数值、DHeff与晶粒尺寸d及气孔率p的关系。
预期在高场区存在DHeff的截止场Hcut,这是因为随磁场的增大自旋波簇上移,当磁场增大到w 出了晶粒表层自旋波簇时DHeff应有的明显下降,实验与之相符[7]。由高场Hcut数据,据
(7)式中DHeff与Ms的反比关系与我们的实验结果
5 能量损耗渠道
由Lax, Sparks, Patton等人建立起来的铁磁弛豫理论的共同特点是:微波能量,不论通过什么途径,都经由一致进动最终传递给晶格,以热能的形式耗散掉。
(7)式在解释DHeff远大于单晶线宽的较高数值、DHeff与晶粒尺寸及气孔率的关系、DHeff的温度特性、DHeff与Ms的反比关系、高场DHeff的截止场以及DHeff(Hi)、S(Hi)曲线等方面的成功[8], 表明了晶粒表层自旋波共振模型是可取的。这说明,在多晶铁氧体材料中微波磁场不仅可以激发一致进动,也可以激发晶粒表层中的自旋波共振。即,实际上还另外存在着一个微波能量经过晶粒表层自旋波系统到达晶格的弛豫过程,见图5中的通道III。特别是在非共振区,由于不存在与一致进动具有相同能量的兼并态自旋波模式,则不可能发生双磁子散射,通道II不通,这时微波能量经过晶粒表层自旋波系统到晶格的弛豫过程(通道III)就成为了能量损耗的主渠道。在细晶粒样品中,由于晶粒表层所占的体积分数较大(d=1 mm时估算值 Vs"40%),这一弛豫机制尤其不可忽略。

6 结论
在微波铁氧体多晶材料中微波磁场不仅可以激发一致进动,也可以激发晶粒表层中的自旋波共振。因而存在着一个由晶粒表层自旋波系统到晶格的弛豫过程。在非共振区,这一弛豫过程是微波能量损耗的主渠道,弛豫时间是tsl;在共振区,由一致进动经过兼并态自旋波到晶格的弛豫过程仍然是微波能量损耗的主渠道,弛豫时间是τud+τdl,主要取决于τud。
在微波铁氧体多晶材料中微波磁场不仅可以激发一致进动,也可以激发晶粒表层中的自旋波共振。因而存在着一个由晶粒表层自旋波系统到晶格的弛豫过程。在非共振区,这一弛豫过程是微波能量损耗的主渠道,弛豫时间是tsl;在共振区,由一致进动经过兼并态自旋波到晶格的弛豫过程仍然是微波能量损耗的主渠道,弛豫时间是τud+τdl,主要取决于τud。
参考文献:
[1] Lax B, Button K J. Microwave ferrite and ferrimagnetics [M]. McGraw Hill, New York, 1962.
[2] Sparks M. Ferromagnetic relaxation theory[M]. MeGraw Hill, New York, 1964.
[3] Patton C E. Microwave resonance and relaxation[M]. Chapter 10 in Magnetic Oxides, D.J. Craik, ed. John Wiley, London, 1975.
[4] Patton C E. Phys Rev 179, 1969, 352.; Patton C E, J Appl Phys. 41, 1970, 1637.
[5] Patton C E. IEEE Trans Magn, MAG-8(3), 1972,433.
[6] Kael berer R E, et al. IEEE Trans Magn. MAG-13, 5, 1977, 1230.
[7] Vrehen Q H F, J Appl Phys, 1996, 40(40): 1849.
[8] Han Z Q. 2002 3rd ICMMT Proc, Beijing, 2002, 1097-1100.
[9] 廖绍彬. 铁磁学(下)[M]. 北京: 科学出版社, 1992, 186.
[10] 钟文定. 铁磁学(中)[M]. 北京: 科学出版社, 1992, 360, 375.
[11] Freidberg R, et al. Phys Rev Letters, 1975, 34(19): 1234.
[12] Hilzinger H R. J Appl Phys 12(3), 1977, 253.
[13] Paul D I. J Appl Phys, 1982, 53(3): 1649, 2362.
[14] Kronmuller H . Proc. II Inter Symp magn Anisotropy and Coercivity in Re-Trans Met Alloys, San Diego(1978).
[15] 韩志全. 物理学报, 1999, 48(12): S291-S297.
[16] 韩志全. 磁性材料及器件, 1999, 30(5): 1-5.
[17] Han Z Q, et al. J Magn Magn Mater, 1986,54: 1192.
[18] Han Z Q, et al. J Appl Phys, 1987, 61(8): 4256.
[19] 韩志全. 科学通报, 1990, 1: 33-35.
[2] Sparks M. Ferromagnetic relaxation theory[M]. MeGraw Hill, New York, 1964.
[3] Patton C E. Microwave resonance and relaxation[M]. Chapter 10 in Magnetic Oxides, D.J. Craik, ed. John Wiley, London, 1975.
[4] Patton C E. Phys Rev 179, 1969, 352.; Patton C E, J Appl Phys. 41, 1970, 1637.
[5] Patton C E. IEEE Trans Magn, MAG-8(3), 1972,433.
[6] Kael berer R E, et al. IEEE Trans Magn. MAG-13, 5, 1977, 1230.
[7] Vrehen Q H F, J Appl Phys, 1996, 40(40): 1849.
[8] Han Z Q. 2002 3rd ICMMT Proc, Beijing, 2002, 1097-1100.
[9] 廖绍彬. 铁磁学(下)[M]. 北京: 科学出版社, 1992, 186.
[10] 钟文定. 铁磁学(中)[M]. 北京: 科学出版社, 1992, 360, 375.
[11] Freidberg R, et al. Phys Rev Letters, 1975, 34(19): 1234.
[12] Hilzinger H R. J Appl Phys 12(3), 1977, 253.
[13] Paul D I. J Appl Phys, 1982, 53(3): 1649, 2362.
[14] Kronmuller H . Proc. II Inter Symp magn Anisotropy and Coercivity in Re-Trans Met Alloys, San Diego(1978).
[15] 韩志全. 物理学报, 1999, 48(12): S291-S297.
[16] 韩志全. 磁性材料及器件, 1999, 30(5): 1-5.
[17] Han Z Q, et al. J Magn Magn Mater, 1986,54: 1192.
[18] Han Z Q, et al. J Appl Phys, 1987, 61(8): 4256.
[19] 韩志全. 科学通报, 1990, 1: 33-35.
如何成为一名优秀的射频工程师,敬请关注: 射频工程师养成培训
上一篇:宽带七端口铁氧体环行器组件的研制
下一篇:微波烘干法测定土料含水率试验修正值研究

